П. 7. Векторное произведение векторов
Градієнт, як завжди вважають, — векторна величина, яка визначає в кожній точці простору не лише швидкість зміни, а й напрямок найшвидшої зміни функції, що залежить від координат. Але при замінах координат, градієнт перетворюється інакше, ніж вектор, і тому його не можна розглядати як справжній вектор.
Градієнт, як завжди вважають, — векторна величина, яка визначає в кожній точці простору не лише швидкість зміни, а й напрямок найшвидшої зміни функції, що залежить від координат. Але при замінах координат, градієнт перетворюється інакше, ніж вектор, і тому його не можна розглядати як справжній вектор.
де і, j, k - орти системи відліку. Приклади · Градієнт скалярного поля · Градієнт скалярного · Градієнт тиску · Градієнт метановості вугільних шахт Прилади: · Градієнтометр гравітаційний · Градієнтометр магнітний
Оператор Даламбера (даламберіан) - диференційний оператор другого порядку.
Дивергенція — скалярне поле, яке характеризує густину джерел даного векторного поля. Дивергенція показує продукується чи поглинається векторне поле в даній точці та визначає інтенсивність цих процесів. Так, наприклад, додатна дивергенція поля швидкостей сталого руху нестискуваної рідини характеризує інтенсивність джерел в даній точці, а від'ємна — інтенсивність стоків. Якщо дивергенція поля дорівнює нулю, то джерел та стоків у цього поля не має. Таке поле називають соленоїдальним. Дивергенцією векторного поля в точці називається границя відношення потоку векторного поля через замкнену поверхню, що охоплює цю точку, до об'єму, обмеженому цією поверхнею, при прямуванні об'єму до нуля:
В декартових координатах, використовуючи формулу Остроградського, дивергенцію поля можна записати в наступному вигляді:
Ротор — вектор, координати якого визначаються визначником третього порядку, перший рядок якого – орти координатних осей, друга – оператори частинного диференціювання в такому ж порядку, як і орти осей, третя – координати функції, яка визначає векторне поле.
З практичної точки зору ротор векторного поля характеризує обертальну здатність поля в даній точці: вона найбільша в даній точці саме в площині, перпендикулярній ротору. Поле, для якого ротор в кожній точці є нульовим вектором, називають потенційним. Якщо v (x, y, z) - поле швидкості руху газу (або течії рідини), то rot v - вектор, пропорційний вектору кутової швидкості дуже маленької та легкої порошинки (або кульки), що знаходиться в потоці. rot v = 2 ω, де ω - кутова швидкість.
П. 7. Векторное произведение векторов Определение. Тройкой векторов называется три вектора Определение. Тройка векторов называется «правой», если кратчайший поворот от вектора
Происхождение названия: если векторы Смысл декартовой тройки
Определение. Векторным произведением векторов 1) Обозначение
|



 де Δ; оператор Лапласа С — константа. Оператор Даламбера є узагальненням оператора Лапласа на випадок простору Мінковського.
де Δ; оператор Лапласа С — константа. Оператор Даламбера є узагальненням оператора Лапласа на випадок простору Мінковського. у декатровій системі координат
у декатровій системі координат









 с общим началом, перечисленных в определенном порядке (
с общим началом, перечисленных в определенном порядке ( - первый,
- первый,  - второй,
- второй,  - третий) и не лежащих в одной плоскости (некомпланарных).
- третий) и не лежащих в одной плоскости (некомпланарных).


 всегда должен соответствовать правилу винта: правый винт (раскручиваем вправо, вкручиваем влево)) – тройка правая, левый винт – тройка левая.
всегда должен соответствовать правилу винта: правый винт (раскручиваем вправо, вкручиваем влево)) – тройка правая, левый винт – тройка левая.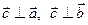 , 2)
, 2)  , 3)
, 3)  или
или  . Это вектор.
. Это вектор.


