Особлива частина

Дата добавления: 2015-06-16; просмотров: 605

Если n – велико, а р – отлично от 0 и 1, то

P(n; k1, k2) 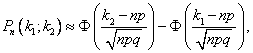где - функция Лапласа (функция табулирована, таблицу можно скачать на странице формул по теории вероятностей).

Функции Гаусса и Лапласа обладают свойствами, которые необходимо знать при использовании таблиц значений этих функций:

а)

б) при больших верно .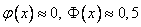

Теоремы Лапласа дают удовлетворительное приближение при . Причем чем ближе значения к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли).

Пример. Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества.

Решение. По условию 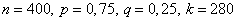, откуда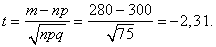

По таблицам найдем .

Искомая вероятность равна:

Пример. В продукции некоторого производства брак составляет 15%. Изделия отправляются потребителям (без проверки) в коробках по 100 штук. Найти вероятности событий:

В – наудачу взятая коробка содержит 13 бракованных изделий;

С – число бракованных изделий в коробке не превосходит 20

Решение. Изготовление детали – это испытание, в котором может появиться событие А – изделие бракованное – с вероятностью 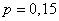. Находим . Можно применять формулы Лапласа:

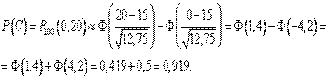
Приблизительно 9,5% всех коробок содержат 13 бракованных изделий и в 92% коробок число бракованных не превосходит 20.

Пример. Небольшой город ежедневно посещают 100 туристов, которые днем идут обедать. Каждый из них выбирает для обеда один из двух городских ресторанов с равными вероятностями и независимо друг от друга. Владелец одного из ресторанов желает, чтобы c вероятностью приблизительно 0,99 все пришедшие в его ресторан туристы могли там одновременно пообедать. Сколько мест должно для этого быть в его ресторане?

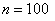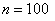Решение. Будем считать, что событие произошло, если турист пообедал у заинтересованного владельца. По условию задачи , . Нас интересует такое наименьшее число посетителей , что вероятность одновременного прихода не менее чем туристов из числа с вероятностью успеха приблизительно равна вероятности переполнения ресторана, т.е. .

Таким образом, нас интересует такое наименьшее число , что . Применим интегральную теорему Муавра-Лапласа.

В нашем случае: – неизвестно, , , . Тогда

Используя таблицы для функции , находим, , и, значит, . Следовательно, в ресторане должно быть 62 места.

Элементы комбинаторики

Рассмотрим некоторое множество Х, состоящее из n элементов . Будем выбирать из этого множества различные упорядоченные подмножества 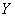из k элементов.

Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор элементов множества Х.

Если выбор элементов множества 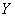из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле (размещения с повторениями).

Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается и определяется равенством

(размещения без повторений).

Пример. Пусть даны шесть цифр: 1; 2; 3; 4; 5; 6. Определить сколько трехзначных чисел можно составить из этих цифр.

Решение. Если цифры могут повторяться, то количество трехзначных чисел будет . Если цифры не повторяются, то .

Пример. Студенты института изучают в каждом семестре по десять дисциплин. В расписание занятий включаются каждый день по 3 дисциплины. Сколько различных расписаний может составить диспетчерская?

Решение. Расписание на каждый день может отличаться либо предметами, либо порядком расположения этих предметов, поэтому имеем размещения:

Частный случай размещения при n=k называется перестановкой из n элементов. Число всех перестановок из n элементов равно
.

Пример. 30 книг стоит на книжной полке, из них 27 различных книг и одного автора три книги. Сколькими способами можно расставить эти книги на полке так, чтобы книги одного автора стояли рядом?

Решение. Будем считать три книги одного автора за одну книгу, тогда число перестановок будет 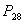. А три книги можно переставлять между собой способами, тогда по правилу произведения имеем, что искомое число способов равно: * 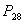=3!*28!

Пусть теперь из множества Х выбирается неупорядоченное подмножество 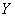(порядок элементов в подмножестве не имеет значения). Сочетаниями из n элементов по kназываются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по k обозначается и равно
.

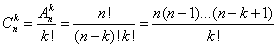Справедливы равенства: , , .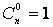

Пример. В группе из 27 студентов нужно выбрать трех дежурных. Сколькими способами можно это сделать?

Решение. Так как порядок студентов не важен, используем формулу для числа сочетаний: .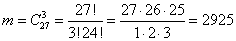

При решении задач комбинаторики используют следующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами.

Пример. Наряд студентки состоит из блузки, юбки и туфель. Девушка имеет в своем гардеробе четыре блузки, пять юбок и трое туфель. Сколько нарядов может иметь студентка?

Решение. Пусть сначала студентка выбирает блузку. Этот выбор может быть совершен четырьмя способами, так как студентка имеет четыре блузки, затем пятью способами произойдет выбор юбки и тремя способами выбор туфель. По принципу умножения получается 4*5*3=60 нарядов (комбинаций).