
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Ку тимчасового користування надрами. Вони також мають право на
Дата добавления: 2015-06-16; просмотров: 636
|
|
· Формула Эйлера.
Пусть 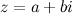 - некоторое комплексное число. По определению полагают, что
- некоторое комплексное число. По определению полагают, что
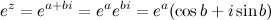
Если число  - действительное, то есть
- действительное, то есть 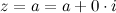 , то
, то
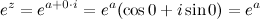
Если число  - чисто мнимое, то есть
- чисто мнимое, то есть 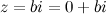 , то
, то
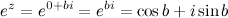
Таким образом, имеем равенство
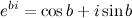
которое называется формулой Эйлера.
· Показательная форма записи комплексного числа.
Рассмотрим произвольное комплексное число, записанное в тригонометрической форме: 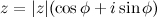 . По формуле Эйлера
. По формуле Эйлера
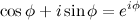
а тогда
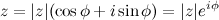
Следовательно, любое комплексное число можно представить в так называемой показательной форме:
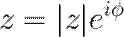
·
Натуральным логарифмом комплексного числа r (cosj + i sinj) называется показатель степени, в которую надо возвысить e, чтобы получить логарифмируемое число. Обозначив натуральный логарифм фимволом Log, можно сказать, что равенство
Log [ r (cosj + i sinj)] = x + yi
равносильно следующему:
ex+yi = r (cosj + i sinj).
Последнее равенство можно написать так:
ex(cos y + i sin y) = r (cosj + i sinj),
откуда, сравнивая модули и аргументы, получим:
ex = r, y = j + 2kp (k = 0, ±1, ±2, ...),
т.е.
x = log r и x + yi = log r + (j + 2kp)i
и окончательно
| Log[ r (cosj + i sinj)] = log r + (j + 2kp)i , | (22) |
т.е. натуральный логарифм комплексного числа равен комплексному числу, вещественная часть которого есть обычный логарифм модуля, а мнимая часть представляет собою произведение i на одно из значений аргумента.
Мы видим, таким образом, что натуральный логарифм любого числа имеет бесчисленное множество значений. Исключение составляет лишь нуль, логарифм которого не существует.
Возведение комплексных чисел в комплексную степень базируется на простой формуле a^b=exp(b ln a)
в частности, (i√5)^(i+1)=exp(i√5 ln(i+1)) = exp(i√5 · (ln √2 + i π/4)) =
= exp (-√5 π / 4 + i √ 5 ln √2) = exp(-√5 π/4) (cos (√5 ln √2) + i sin (√5 ln √2))
возведение в степень на множестве комплексных чисел определено неоднозначно, так как значение ln a определено с точностью до слагаемого i 2π
Экспоне́нта — показательная функция 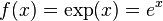 , где е — Число Эйлера (
, где е — Число Эйлера ( 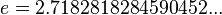 ).
).
| <== предыдущая лекция | | | следующая лекция ==> |
| Нафтою 1992 року; | | | Ночас небезпечний для навколишнього природного середовища та |