
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Недедуктивна (правдоподібна) аргументація
Дата добавления: 2015-08-30; просмотров: 866
|
|
Задача 16. Используя данные о молочной продуктивности коров кг/день была сформирована 5% выборка из 150 коров человек.
Таблица 54
| Показатель | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 |
| Надой, кг/день | 13,98 | 13,92 | 14,42 | 13,76 | 14,16 |
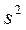
| 0,98617 | 1,05396 | 0,58081 | 1,13664 | 0,99436 |
| Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 | |
| Надой, кг/день | 14,1 | 14,06 | 13,98 | 14,12 | 14,06 |
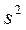
| 0,82886 | 1,03664 | 0,97275 | 0,71034 | 0,99638 |
| Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 | |
| Надой, кг/день | 14,28 | 13,92 | 14,24 | 13,72 | 14,18 |
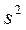
| 0,61906 | 1,04054 | 0,78765 | 1,20966 | 0,90027 |
Необходимо определить
1. Для случайного бесповторного отбора:
· среднюю и предельную (с вероятностью 0,954 (при 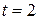 )) ошибку выборки;
)) ошибку выборки;
· на сколько необходимо изменить численность выборки, чтобы средняя, предельная ошибка изменилась до (табл. 55):
Таблица 55
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 |
| ±0,1 | ±0,06 | ±0,15 | ±0,9 | ±0,11 |
| Вариант 6 | Вариант 7 | Вариант 8 | Вариант 9 | Вариант 10 |
| ±0,2 | ±0,07 | ±0,3 | ±0,19 | ±0,13 |
| Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 |
| ±0,65 | ±0,2 | ±0,04 | ±0,01 | ±0,03 |
2. Повторить расчеты для случайного повторного отбора.
Задача 17. Методом бесповторного отбора из общей численности молочного стада была проведена 5% выборка.
Таблица 56
| № варианта | Численность выборки

| Доля коров старше 5лет в выборке
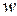
| Уровень доверительной вероятности
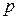
| № варианта | Численность выборки

| Доля коров старше 5лет в выборке
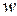
| Уровень доверительной вероятности
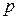
|
| 0,3 | 0,7287 | 0,3 | 0,9426 | ||||
| 0,2 | 0,7699 | 0,3 | 0,9545 | ||||
| 0,3 | 0,8064 | 0,2 | 0,9643 | ||||
| 0,3 | 0,8385 | 0,3 | 0,9836 | ||||
| 0,2 | 0,9426 | 0,2 | 0,9876 | ||||
| 0,3 | 0,9545 | 0,2 | 0,9907 | ||||
| 0,3 | 0,9643 | 0,3 | 0,9109 | ||||
| 0,1 | 0,9836 | 0,3 | 0,9281 | ||||
| 0,2 | 0,9876 | 0,2 | 0,9426 | ||||
| 0,3 | 0,9907 | 0,3 | 0,9545 |
Определить с заданной вероятностью 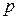 пределы, в которых находится доля коров старше 5лет. Повторить расчет для повторного отбора.
пределы, в которых находится доля коров старше 5лет. Повторить расчет для повторного отбора.
Задача 18. По району имеются данные об общей численности молочного стада КРС.
Таблица 57
| № варианта | Численность генеральной совокупности, гол.

| Уровень доверительной вероятности
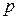
| Стандартная ошибка
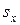
| № варианта | Численность генеральной совокупности, гол.

| Уровень доверительной вероятности
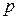
| Стандартная ошибка
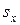
|
| 0,7287 | 1,1 | 0,9426 | 1,3 | ||||
| 0,7699 | 1,2 | 0,9545 | 1,2 | ||||
| 0,8064 | 1,2 | 0,9643 | 1,3 | ||||
| 0,8385 | 1,1 | 0,9836 | 1,3 | ||||
| 0,9426 | 1,3 | 0,9876 | 1,2 | ||||
| 0,9545 | 1,2 | 0,9907 | 1,1 | ||||
| 0,9643 | 1,3 | 0,9109 | 1,1 | ||||
| 0,9836 | 1,3 | 0,9281 | 1,2 | ||||
| 0,9876 | 1,2 | 0,9426 | 1,2 | ||||
| 0,9907 | 1,1 | 0,9545 | 1,1 |
Необходимо определить численность выборки с заданной вероятностью 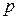 , предельная ошибка среднего надоя не должна превышать 0,2 кг .
, предельная ошибка среднего надоя не должна превышать 0,2 кг .
Задача 19. По области изучается доля хозяйств урожайность, в которых превышает 22ц/га. Известно, что:
Таблица 58
| № варианта | Численность генеральной совокупности, гол.

| Уровень доверительной вероятности
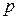
| Доля хозяйств с урожайностью более 22ц/га. | № варианта | Численность генеральной совокупности, гол.

| Уровень доверительной вероятности
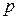
| Доля хозяйств с урожайностью более 22ц/га. |
| 0,7287 | 0,5 | 0,9426 | 0,4 | ||||
| 0,7699 | 0,6 | 0,9545 | 0,3 | ||||
| 0,8064 | 0,7 | 0,9643 | 0,6 | ||||
| 0,8385 | 0,8 | 0,9836 | 0,8 | ||||
| 0,9426 | 0,4 | 0,9876 | 0,4 | ||||
| 0,9545 | 0,6 | 0,9907 | 0,6 | ||||
| 0,9643 | 0,5 | 0,9109 | 0,5 | ||||
| 0,9836 | 0,4 | 0,9281 | 0,7 | ||||
| 0,9876 | 0,8 | 0,9426 | 0,4 | ||||
| 0,9907 | 0,4 | 0,9545 | 0,5 |
Необходимо определить необходимую численность выборки для бесповторного и повторного отборов.
| <== предыдущая лекция | | | следующая лекция ==> |
| Дедуктивна аргументація | | | Пряма та непряма аргументація |