
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Пряма та непряма аргументація
Дата добавления: 2015-08-30; просмотров: 793
|
|
Задача 20. Имеются данные о величине результативного признака 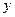 и факторного признака
и факторного признака 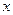
Таблица 59
| № | Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | Вариант 5 | |||||
| у | х | у | х | у | х | у | х | у | х | |
| 10,49 | 67,00 | 12,57 | 87,00 | 15,50 | 1,02 | 9,86 | 54,00 | 0,76 | 18,21 | |
| 8,57 | 53,00 | 10,93 | 65,00 | 16,34 | 0,44 | 7,39 | 48,00 | 1,06 | 19,17 | |
| 10,95 | 70,00 | 9,86 | 54,00 | 17,13 | 1,22 | 9,23 | 61,00 | 1,06 | 20,42 | |
| 9,23 | 51,00 | 7,39 | 48,00 | 17,10 | 0,72 | 15,40 | 79,00 | 0,52 | 20,00 | |
| 11,97 | 70,00 | 9,23 | 61,00 | 27,16 | 1,59 | 13,14 | 85,00 | 0,99 | 20,37 | |
| 8,56 | 56,00 | 15,40 | 79,00 | 14,92 | 1,23 | 13,12 | 83,00 | 0,67 | 21,04 | |
| 12,18 | 55,00 | 13,14 | 85,00 | 18,17 | 0,82 | 10,27 | 64,00 | 1,02 | 20,25 | |
| 7,93 | 47,00 | 13,12 | 83,00 | 17,24 | 0,98 | 9,12 | 55,00 | 0,44 | 17,68 | |
| 15,75 | 89,00 | 10,27 | 64,00 | 14,64 | 0,41 | 13,42 | 72,00 | 1,22 | 28,19 | |
| 13,61 | 74,00 | 9,12 | 55,00 | 14,70 | 0,79 | 10,29 | 69,00 | 0,72 | 22,63 | |
| 13,99 | 52,00 | 13,42 | 72,00 | 28,81 | 1,20 | 11,55 | 72,00 | 1,59 | 40,16 | |
| 12,57 | 87,00 | 10,29 | 69,00 | 21,87 | 0,99 | 15,26 | 87,00 | 1,23 | 21,12 | |
| 10,93 | 65,00 | 11,55 | 72,00 | 16,88 | 0,91 | 12,35 | 79,00 | 0,82 | 26,01 | |
| 9,86 | 54,00 | 15,26 | 87,00 | 16,65 | 0,83 | 8,24 | 49,00 | 0,98 | 17,99 | |
| 7,39 | 48,00 | 12,35 | 79,00 | 16,10 | 0,81 | 10,41 | 64,00 | 0,41 | 21,90 | |
| 9,23 | 61,00 | 8,24 | 49,00 | 18,02 | 1,21 | 9,62 | 52,00 | 0,79 | 20,47 | |
| 15,4 | 79,00 | 10,41 | 64,00 | 16,91 | 0,78 | 10,76 | 65,00 | 1,20 | 29,01 | |
| 13,14 | 85,00 | 9,62 | 52,00 | 14,90 | 0,86 | 8,35 | 51,00 | 0,99 | 23,40 | |
| 13,12 | 83,00 | 10,76 | 65,00 | 17,64 | 1,21 | 10,31 | 75,00 | 0,91 | 25,53 | |
| 10,27 | 64,00 | 8,35 | 51,00 | 14,41 | 1,20 | 9,38 | 55,00 | 0,83 | 21,18 | |
| 9,12 | 55,00 | 10,31 | 75,00 | 12,62 | 1,07 | 14,93 | 72,00 | 0,81 | 20,24 |
Продолжение табл. 59
| 13,42 | 72,00 | 9,38 | 55,00 | 18,13 | 0,79 | 12,46 | 79,00 | 1,21 | 20,22 | |
| 10,29 | 69,00 | 14,93 | 72,00 | 17,30 | 0,77 | 10,45 | 59,00 | 0,78 | 24,89 | |
| 11,55 | 72,00 | 12,46 | 79,00 | 17,16 | 0,82 | 12,38 | 80,00 | 0,86 | 20,86 | |
| 15,26 | 87,00 | 10,45 | 59,00 | 14,65 | 0,63 | 7,74 | 76,00 | 1,21 | 28,42 | |
| Итого | 284,78 | 1665,00 | 278,81 | 1681,00 | 434,95 | 23,30 | 275,43 | 1685,00 | 23,08 | 569,36 |
| В среднем | 11,39 | 66,60 | 11,15 | 67,24 | 17,40 | 0,93 | 11,02 | 67,40 | 0,92 | 22,77 |
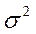
| 2,3558206 | 12,94604 | 2,157942 | 12,169733 | 3,5855599 | 0,2631957 | 2,2543585 | 11,90966 | 0,267802 | 4,751135 |
| № | Вариант 6 | Вариант 8 | Вариант 9 | Вариант 10 | ||||||
| у | х | у | х | у | х | у | х | у | х | |
| 11,30 | 67,00 | 405,00 | 67,00 | 405,00 | 15,75 | 33,50 | 700,00 | 47,00 | 33,50 | |
| 11,50 | 53,00 | 456,00 | 53,00 | 456,00 | 15,40 | 36,80 | 640,00 | 48,00 | 36,80 | |
| 11,60 | 70,00 | 456,00 | 70,00 | 456,00 | 15,26 | 31,20 | 660,00 | 51,00 | 31,20 | |
| 11,10 | 51,00 | 457,00 | 51,00 | 457,00 | 13,99 | 36,80 | 655,00 | 52,00 | 36,80 | |
| 9,90 | 70,00 | 462,00 | 70,00 | 462,00 | 13,61 | 37,30 | 685,00 | 53,00 | 37,30 | |
| 11,70 | 56,00 | 469,00 | 56,00 | 469,00 | 13,42 | 37,80 | 672,00 | 54,00 | 37,80 | |
| 11,90 | 55,00 | 492,00 | 55,00 | 492,00 | 13,14 | 36,40 | 679,00 | 55,00 | 36,40 | |
| 11,80 | 47,00 | 501,00 | 47,00 | 501,00 | 13,12 | 37,90 | 700,00 | 55,00 | 37,90 | |
| 11,90 | 70,00 | 506,00 | 70,00 | 506,00 | 12,57 | 39,00 | 700,00 | 56,00 | 39,00 | |
| 12,50 | 74,00 | 512,00 | 74,00 | 512,00 | 12,35 | 40,00 | 690,00 | 61,00 | 40,00 | |
| 11,70 | 52,00 | 536,00 | 52,00 | 536,00 | 12,18 | 40,10 | 698,00 | 64,00 | 41,01 | |
| 12,60 | 87,00 | 539,00 | 87,00 | 539,00 | 11,97 | 40,60 | 699,00 | 65,00 | 40,60 | |
| 12,90 | 65,00 | 568,00 | 65,00 | 568,00 | 11,55 | 40,50 | 701,00 | 67,00 | 40,50 | |
| 12,90 | 54,00 | 569,00 | 54,00 | 569,00 | 10,93 | 40,80 | 712,00 | 69,00 | 40,80 |
Продолжение табл. 59
| 12,50 | 48,00 | 572,00 | 48,00 | 572,00 | 10,41 | 40,90 | 715,00 | 70,00 | 40,90 | |
| 13,00 | 61,00 | 578,00 | 61,00 | 578,00 | 10,29 | 41,30 | 716,00 | 70,00 | 41,30 | |
| 13,50 | 79,00 | 579,00 | 79,00 | 579,00 | 10,27 | 41,50 | 730,00 | 70,00 | 41,50 | |
| 13,00 | 85,00 | 581,00 | 85,00 | 581,00 | 9,86 | 41,90 | 760,00 | 72,00 | 41,90 | |
| 12,90 | 83,00 | 586,00 | 83,00 | 586,00 | 9,62 | 42,00 | 710,00 | 72,00 | 42,00 | |
| 13,40 | 64,00 | 591,00 | 64,00 | 591,00 | 9,23 | 42,10 | 730,00 | 74,00 | 42,10 | |
| 13,90 | 55,00 | 599,00 | 55,00 | 599,00 | 9,12 | 41,50 | 736,00 | 79,00 | 41,50 | |
| 14,00 | 72,00 | 630,00 | 72,00 | 630,00 | 8,56 | 42,50 | 780,00 | 83,00 | 42,50 | |
| 13,50 | 69,00 | 638,00 | 69,00 | 638,00 | 8,24 | 42,60 | 787,00 | 84,00 | 42,60 | |
| 13,90 | 72,00 | 649,00 | 72,00 | 649,00 | 7,93 | 43,10 | 790,00 | 85,00 | 43,10 | |
| 14,20 | 80,00 | 656,00 | 84,00 | 656,00 | 7,39 | 43,50 | 820,00 | 87,00 | 43,50 | |
| Итого | 313,10 | 1639,00 | 13587,00 | 1643,00 | 13587,00 | 286,16 | 955,51 | 17865,00 | 1643,00 | 992,51 |
| В среднем | 12,52 | 65,56 | 543,48 | 65,72 | 543,48 | 11,45 | 38,22 | 714,60 | 65,72 | 39,70 |
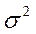
| 1,0450952 | 11,72375 | 67,63557 | 11,94494 | 67,635565 | 2,3662931 | 7,594513 | 43,51643 | 11,94494 | 2,997239 |
| № | Вариант 11 | Вариант 12 | Вариант 13 | Вариант 14 | Вариант 15 | |||||
| у | х | у | х | у | х | у | х | у | х | |
| 1300,00 | 44,00 | 44,00 | 902,00 | 1300,00 | 902,00 | 902,00 | 33,50 | 33,50 | 44,00 | |
| 1320,00 | 46,00 | 46,00 | 905,00 | 1320,00 | 905,00 | 905,00 | 36,80 | 36,80 | 46,00 | |
| 1350,00 | 54,00 | 54,00 | 904,00 | 1350,00 | 904,00 | 904,00 | 31,20 | 31,20 | 54,00 | |
| 1360,00 | 57,00 | 57,00 | 900,00 | 1360,00 | 900,00 | 900,00 | 36,80 | 36,80 | 57,00 | |
| 1370,00 | 61,00 | 61,00 | 885,00 | 1370,00 | 885,00 | 885,00 | 37,30 | 37,30 | 61,00 | |
| 1378,00 | 47,00 | 47,00 | 882,00 | 1378,00 | 882,00 | 882,00 | 37,80 | 37,80 | 47,00 | |
| 1390,00 | 55,00 | 55,00 | 880,00 | 1390,00 | 880,00 | 880,00 | 36,40 | 36,40 | 55,00 |
Окончание табл. 59
| 1400,00 | 50,00 | 50,00 | 761,00 | 1400,00 | 761,00 | 761,00 | 37,90 | 37,90 | 50,00 | |
| 1410,00 | 64,00 | 64,00 | 783,00 | 1410,00 | 783,00 | 783,00 | 39,00 | 39,00 | 64,00 | |
| 1420,00 | 55,00 | 55,00 | 752,00 | 1420,00 | 752,00 | 752,00 | 40,00 | 40,00 | 55,00 | |
| 1430,00 | 72,00 | 72,00 | 750,00 | 1430,00 | 750,00 | 750,00 | 40,01 | 40,01 | 72,00 | |
| 1436,00 | 49,00 | 49,00 | 746,00 | 1436,00 | 746,00 | 746,00 | 40,60 | 40,60 | 49,00 | |
| 1439,00 | 51,00 | 51,00 | 740,00 | 1439,00 | 740,00 | 740,00 | 40,50 | 40,50 | 51,00 | |
| 1439,00 | 52,00 | 52,00 | 730,00 | 1439,00 | 730,00 | 730,00 | 40,80 | 40,80 | 52,00 | |
| 1440,00 | 55,00 | 55,00 | 710,00 | 1440,00 | 710,00 | 710,00 | 40,90 | 40,90 | 55,00 | |
| 1443,00 | 59,00 | 59,00 | 725,00 | 1443,00 | 725,00 | 725,00 | 41,30 | 41,30 | 59,00 | |
| 1446,00 | 64,00 | 64,00 | 730,00 | 1446,00 | 730,00 | 730,00 | 41,50 | 41,50 | 64,00 | |
| 1449,00 | 65,00 | 65,00 | 710,00 | 1449,00 | 710,00 | 710,00 | 41,90 | 41,90 | 65,00 | |
| 1530,00 | 69,00 | 69,00 | 704,00 | 1530,00 | 704,00 | 704,00 | 42,00 | 42,00 | 69,00 | |
| 1594,00 | 72,00 | 72,00 | 700,00 | 1594,00 | 700,00 | 700,00 | 42,10 | 42,10 | 72,00 | |
| 1599,00 | 72,00 | 72,00 | 685,00 | 1599,00 | 685,00 | 685,00 | 41,50 | 41,50 | 72,00 | |
| 1620,00 | 75,00 | 75,00 | 610,00 | 1620,00 | 610,00 | 610,00 | 42,50 | 42,50 | 75,00 | |
| 1630,00 | 79,00 | 79,00 | 600,00 | 1630,00 | 600,00 | 600,00 | 42,60 | 42,60 | 79,00 | |
| 1650,00 | 79,00 | 79,00 | 590,00 | 1650,00 | 590,00 | 590,00 | 43,10 | 43,10 | 79,00 | |
| 1680,00 | 87,00 | 87,00 | 505,00 | 1680,00 | 505,00 | 505,00 | 43,50 | 43,50 | 87,00 | |
| Итого | 36523,00 | 1533,00 | 1533,00 | 18789,00 | 36523,00 | 18789,00 | 18789,00 | 991,51 | 991,51 | 1533,00 |
| В среднем | 1460,92 | 61,32 | 61,32 | 751,56 | 1460,92 | 751,56 | 751,56 | 39,66 | 39,66 | 61,32 |
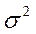
| 105,68706 | 11,50902 | 11,50902 | 107,39724 | 105,68706 | 107,39724 | 107,39724 | 2,986147 | 2,986147 | 11,50902 |
Необходимо:
1. Рассчитать коэффициент парной линейной корреляции, парной линейной детерминации, сделать выводы по каждому коэффициенту.
2. Построить уравнение парной линейной регрессии, спрогнозировать 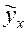 при различных значениях фактора, то есть рассчитать:
при различных значениях фактора, то есть рассчитать:
· максимально возможную величину 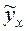 ;
;
· минимальную 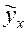 ;
;
· 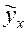 для средних значений фактора.
для средних значений фактора.
2. Провести статистическую оценку:
· уравнения регрессии;
· параметров уравнения регрессии.
Таблица 60
Варианты контрольных заданий
| А | ||||||||||||||
| Вариант | Задача | Вопросы | Вариант | Задача | Вопросы | Вариант | Задача | Вопросы | Вариант | Задача | Вопросы | Вариант | Задача | Вопросы |
| 17-1 | 3, 98, 228 | 2-10 | 47, 138, 268 | 5-4 | 42, 104, 264 | 12-4 | 75, 135, 142 | 9-4 | 298, 166, 79 | |||||
| 19-2 | 46, 168, 300 | 20-1 | 48, 139, 237 | 5-5 | 72, 140, 270 | 10-5 | 299, 167, 76 | 9-5 | 297, 199, 80 | |||||
| 16-2 | 296, 196, 15 | 3-2 | 132, 257, 2 | 6-1 | 294, 171, 6 | 18-6 | 293, 201, 7 | 9-6 | 291, 173, 9 | |||||
| 17-6 | 290, 229, 10 | 8-3 | 267, 226, 29 | 6-2 | 265, 231, 30 | 12-7 | 262, 232, 31 | 19-7 | 261, 195, 34 | |||||
| 18-4 | 259, 19, 160 | 16-4 | 285, 152, 56 | 18-3 | 314, 153, 51 | 12-8 | 252, 90, 22 | 10-1 | 309, 182, 24 | |||||
| 1-5 | 316, 119, 50 | 3-5 | 219, 117, 21 | 6-4 | 280, 149, 20 | 13-1 | 313, 178, 23 | 20-2 | 278, 118, 54 | |||||
| 17-6 | 312, 185, 27 | 3-6 | 286, 150, 28 | 6-5 | 284, 120, 29 | 20-2 | 220, 26, 287 | 10-3 | 25, 315, 123 | |||||
| 15-7 | 6, 100, 133 | 16-7 | 283, 151, 30 | 7-1 | 282, 154, 31 | 17-3 | 281, 155, 32 | 18-4 | 277, 156, 55 | |||||
| 1-8 | 275, 146, 53 | 3-8 | 279, 147, 52 | 7-2 | 83, 183, 251 | 13-4 | 271, 116, 59 | 10-5 | 276, 157, 57 |
Окончание табл. 60
| А | ||||||||||||||
| 1-9 | 67, 230, 289 | 3-9 | 9, 69, 288 | 7-3 | 2, 260, 99 | 11-5 | 246, 144, 60 | 10-6 | 273, 145, 58 | |||||
| 1-10 | 7, 70, 292 | 3-10 | 243, 213, 91 | 7-4 | 253, 186, | 13-6 | 248, 115, 81 | 18-7 | 243, 112, 61 | |||||
| 15-1 | 164, 1, 66 | 18-1 | 37, 162, 227 | 19-5 | 256,3, 16 | 13-7 | 58, 224, 161 | 11-2 | 214, 181, 62 | |||||
| 19-2 | 193, 9, 312 | 4-2 | 194, 12, 285 | 8-1 | 6, 192,34 | 5-1 | 234, 9, 74 | 11-3 | 255, 121, 63 | |||||
| 20-3 | 8, 211, 78 | 3-3 | 163, 65, 3 | 8-2 | 165, 12, 304 | 14-2 | 249, 158, 86 | 13-4 | 254, 179, 64 | |||||
| 2-4 | 11, 318, 76 | 8-4 | 198, 43, 272 | 13-3 | 250, 188, 85 | 14-3 | 247, 210, 87 | 11-5 | 244, 187, 89 | |||||
| 15-5 | 41, 97, 304 | 4-5 | 245, 180, 88 | 8-4 | 200, 4, 78 | 14-4 | 177, 18, 65 | 11-6 | 302, 39, 169 | |||||
| 2-6 | 49, 303, 136 | 15-6 | 73, 8, 295 | 20-5 | 202, 64, 12 | 15-5 | 128, 305, 15 | 11-7 | 203, 17, 68 | |||||
| 2-7 | 310, 10, 5 | 5-1 | 269, 71, 16 | 9-1 | 307, 170, 13 | 19-6 | 208, 34, 137 | 12-1 | 306, 113, 38 | |||||
| 18-8 | 240, 96, 35 | 5-2 | 308, 141, 77 | 9-2 | 274, 14, 101 | 14-7 | 103, 301, 36 | 12-2 | 266, 44, 102 | |||||
| 2-9 | 172, 11, 204 | 5-3 | 263, 33, 84 | 9-3 | 108, 19, 233 | 14-8 | 45, 235, 17 | 18-3 | 205, 40, 82 |
Вопросы к тестам
1. В настоящее время термин «статистика» означает:
а) отрасль практической деятельности, которая имеет целью сбор, обработку, анализ и публикацию массовых данных о различных явлениях общественной жизни, «статистический учет»;
б) цифровой материал, который характеризует общественные явления или территориальные распределения какого-либо признака;
в) отрасль знания, научную дисциплину, учебный предмет;
г) а, б, в.
2. Предметом статистики является:
а) качественная сторона массовых общественных явлений в связи с их количественной стороной;
б) лишь качественная сторона массовых общественных явлений;
в) лишь количественная сторона массовых общественных явлений.
3. Статистическая совокупность – это:
а) масса произвольно отобранных единиц;
б) масса единиц объединенных единой качественной стороной;
в) масса единиц полученных в результате произвольного статистического наблюдения.
4. Статистический признак – это:
а) количественная особенность единицы совокупности;
б) качественная особенность единицы совокупности;
в) количественная особенность статистической совокупности;
г) качественная особенность статистической совокупности.
5. Статистический показатель – это:
а) количественная особенность единицы совокупности;
б) качественная особенность единицы совокупности;
в) количественная особенность статистической совокупности;
г) понятие (категория), отображающее количественные характеристики (размеры) статистической совокупности, имеющее качественную определенность.
6. Метод статистики включает:
а) метод массовых наблюдений;
б) метод группировок;
в) метод обобщающих показателей;
г) метод измеряющих показателей;
д) а, б, в;
е) а, б, в, г.
7. Статистическое наблюдение – это:
а) первый этап статистического анализа;
б) второй этап статистического анализа;
в) третий этап статистического анализа;
г) четвертый этап статистического анализа.
8. Статистическое наблюдение осуществляется в форме:
а) предоставления плановой отчетности;
б) проведения специально организованного наблюдения;
в) а, б.
9. Единицей наблюдения называют:
а) первичный элемент объекта, который является непосредственным носителем признаков, подлежащих наблюдению;
б) единица, от которой должны быть получены сведения в процессе наблюдения;
в) а, б.
10. Статистическая сводка – это:
а) первый этап статистического анализа;
б) второй этап статистического анализа;
в) трений этап статистического анализа;
г) четвертый этап статистического анализа.
11. Сводка называется простой, если:
а) в ней отсутствуют группировки;
б) в ней присутствуют только простые группировки;
в) в ней присутствуют только сложные группировки;
г) группировка присутствует, но игнорируется;
д) а, б.
12. Статистическая группировка – это:
а) объединение в группы разнородных показателей;
б) разбиение совокупности на группы, однородные по какому-то признаку;
в) объединение в группы однородных и разнородных показателей;
г) а, б.
13. Группировочный признак:
а) признак, по которому происходит объединение двух и более совокупностей;
б) признак, по которому происходит разделение совокупности на группы;
в) признак, исключающийся из совокупности.
14. Группировочные интервал:
а) промежуток между двумя крайними значениями группировочного признака, очерчивает границы групп;
б) промежуток между двумя крайними значениями группировочного признака, очерчивает границы изучаемой совокупности;
в) промежуток между двумя любыми значениями группировочного признака, не очерчивает границ групп и совокупности.
15. Группировочный интервалы бывают:
а) равные; б) неравные;
в) открытые; г) закрытые;
д) а, б; е) в, г;
ж) а, б, в, г.
16. Величина интервала зависит от:
а) вариации признака в изучаемой совокупности;
б) количества единиц в изучаемой совокупности;
в) а, б.
17. Группировка называется простой, если:
а) все признаки, по которым она построена, не нуждаются в дополнительных расчетах;
б) один из признаков, по которым она построена, не нуждается в дополнительных расчетах;
в) она выполнена по одному признаку;
г) она выполнена по двум и более признакам;
д) а, б; е) в, г; ж) а, б, в, г.
18. Иерархическая группировка:
а) многомерная группировка, в которой значение последующего признака определяется областью значений предыдущего;
б) многомерная группировка, в которой значение предыдущего признака определяется областью значений последующего;
в) зависимости между признаками нет.
19. Типологическая группировка:
а) расчленение совокупности на группы, характеризующие ее строение;
б) разбиение исследуемой совокупности на социально-экономические классы;
в) позволяет охарактеризовать взаимосвязи между изучаемыми признаками.
20. Структурная группировка:
а) расчленение совокупности на группы, характеризующие ее строение;
б) разбиение исследуемой совокупности на социально-экономические классы;
в) позволяет охарактеризовать взаимосвязи между изучаемыми признаками.
21. Аналитическая группировка:
а) расчленение совокупности на группы, характеризующие ее строение;
б) разбиение исследуемой совокупности на социально-экономические классы;
в) позволяет охарактеризовать взаимосвязи между изучаемыми признаками.
22. Статистические графики:
а) условное обозначение числовых величин и их соотношений в виде графических (геометрических) образов – точек, линий, плоскостных фигур, их сочетаний и различного расположения;
б) условное обозначение числовых величин и их соотношений в виде линий
в) статистика пользуется специфическими методами изображения графиков.
23. Возрастающим графиком называется график, на котором:
а) возрастанию значений на оси X соответствует возрастание значений на оси Y;
б) возрастанию значений на оси Х соответствует убывание значений на оси Y;
в) а, б.
24. Убывающим графиком называется график, на котором:
а) возрастанию значений на оси X соответствует возрастание значений на оси Y;
б) возрастанию значений на оси Х соответствует убывание значений на оси Y;
в) а, б.
25. Кривой огива называется:
а) С-образная кривая;
б) V-образная кривая;
в) S-образная кривая.
26. Ось абсцисс (Х):
а) делит поле графика по диагонали;
б) обычно вертикальная линия;
в) обычно горизонтальная линия.
27. Ось ординат (Y):
а) обычно горизонтальная линия;
б) обычно вертикальная линия;
в) делит поле графика по диагонали.
28. Статистические таблицы – это:
а) таблицы для расчетов;
б) вспомогательные математико-вычислительные таблицы;
в) таблицы для наглядного изображения результатов исследования;
г) справочные таблицы;
д) б, в; е) а, в.
29. Строкой таблицы называется:
а) расположенная по горизонтали полоса;
б) расположенная по вертикали полоса;
в) зависит от угла поворота зрения;
г) а, б.
30. Графой таблицы называется:
а) расположенная по горизонтали полоса;
б) расположенная по вертикали полоса;
в) зависит от угла поворота зрения;
г) а, б.
31. Сказуемое таблицы – это:
а) содержит объект наблюдения, то есть перечень единиц совокупности, укрупненных единиц совокупности или групп;
б) перечень граф и диаграмм таблицы;
в) непосредственно числовые данные.
32. Подлежащее таблицы –это:
а) содержит объект наблюдения, то есть перечень единиц совокупности, укрупненных единиц совокупности или групп;
б) перечень граф и диаграмм таблицы;
в) непосредственно числовые данные.
33. Обобщающая характеристика какого-то свойства совокупности, группы – это:
а) статистический признак;
б) статистический показатель;
в) статистические данные;
г) а, в.
34. Надпись «Итого» обозначает:
а) итог для части совокупности;
б) итог для всей совокупности в целом;
в) а, б.
35. Надпись «Всего» обозначает:
а) итог для части совокупности;
б) итог для всей совокупности в целом;
в) а, б.
36. Знак тире (–) – ставится, когда:
а) явление не имеет осмысленного содержания;
б) явление отсутствует;
в) отсутствуют сведения;
г) имеющие сведения имеют размеры меньше принятой в таблице точности.
37. Знак (х) ставится, когда:
а) явление не имеет осмысленного содержания;
б) явление отсутствует;
в) отсутствуют сведения;
г) имеющие сведения имеют размеры меньше принятой в таблице точности.
38. Многоточие (…) ставится, когда:
а) явление не имеет осмысленного содержания;
б) явление отсутствует;
в) отсутствуют сведения;
г) имеющие сведения имеют размеры меньше принятой в таблице точности.
39. Дробное число (0,0) ставится, когда:
а) явление не имеет осмысленного содержания;
б) явление отсутствует;
в) отсутствуют сведения;
г) имеющие сведения имеют размеры меньше принятой в таблице точности.
40. Статистические данные – это:
а) обобщающая характеристика какого-то свойства совокупности, группы;
б) обобщающая характеристика единицы совокупности, группы;
в) конкретное численное значение;
г) а, в.
41. Абсолютные статистические показатели измеряются:
а) в конкретных единицах измерения;
б) в относительных единицах измерения;
в) а, б.
42. Относительные статистические показатели измеряются:
а) в конкретных единицах измерения;
б) в относительных единицах измерения;
в) а, б.
43. Если в ходе расчета относительных статистических показателей величина, принятая за базу сравнения, приравнивается к единице, то форма относительной величины называться:
а) коэффициент; б) темп; в) промилле; г) продецимилле.
44. Если в ходе расчета относительных статистических показателей величина, принятая за базу сравнения, приравнивается к 100, то форма относительной величины называться:
а) коэффициент; б) темп; в) промилле; г) продецимилле.
45. Если в ходе расчета относительных статистических показателей величина, принятая за базу сравнения, приравнивается к 1000, то форма относительной величины называться:
а) коэффициент; б) темп; в) промилле; г) продецимилле.
46. Если в ходе расчета относительных статистических показателей величина, принятая за базу сравнения, приравнивается к 10000, то форма относительной величины называться:
а) коэффициент; б) темп; в) промилле; г) продецимилле.
47. Абсолютные показатели, по способу измерения бывают:
а) натуральные;
б) условно-натуральные;
в) стоимостные;
г) а, в; д) а, б, в.
48. Средние величины характеризуют:
а) меру и степень вариации совокупности;
б) центр распределения;
в) форму (тип) распределения;
г) а, б, в.
49. Основные правила построения средних:
а) необходимо массовое обобщение фактов;
б) качественная однородность совокупности;
в) все единицы должны быть одинаковы;
г) а, б, в; д) а, в; е) б, в.
50. Средняя не рассчитывается по:
а) двум единицам;
б) более чем по трем единицам;
в) по всем выборочным совокупностям;
51. Общая формула расчета степенных средних имеет вид:
а) 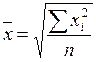 ; б)
; б) 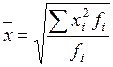 ; в)
; в) 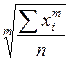 ; г)
; г) 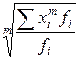 ;
;
д) а, б; е) в,г.
52. Всего степенных средних можно рассчитать:
а) 3; б) 5;
в) от 0 до + ∞;
г) от 0 до - ∞;
д) от - ∞ до + ∞.
53. Вид степенной средней зависит от:
а) количества единиц в совокупности;
б) показателя степени;
в) назначается произвольно.
54. Средние степенные простые применяют для расчета:
а) сгруппированных данных;
б) несгруппированных данных;
в) а, б.
55. Средние степенные взвешенные применяют для расчета:
а) сгруппированных данных;
б) несгруппированных данных;
в) а, б.
56. Формула средней арифметической имеет вид:
а) 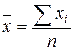 ; б)
; б) 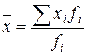 ; в)
; в) 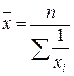 ; г)
; г) 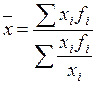 .
.
Д) а, б; е) в, г; ж) а, в; з) б, г.
57. Формула средней гармонической имеет вид:
а) 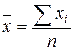 ; б)
; б) 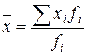 ; в)
; в) 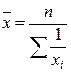 ; г)
; г) 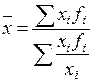 ;
;
д) а, б; е) в, г; ж) а, в; з) б, г.
58. Формула средней квадратической имеет вид:
а) 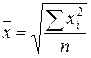 ; б);
; б); 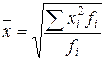 ; в);
; в); 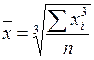 ; г)
; г) 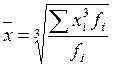 ;
;
д) а, б; е) в, г; ж) а, в; з) б, г.
59. Средняя геометрическая применяется для расчета:
а) средних коэффициентов роста;
б) средних коэффициентов прироста;
в) средних уровней динамических рядов;
г) средних уровней статических рядов;
д) а, б; е) в, г.
60. Если к каждой варианте прибавить или отнять одно и то же постоянное число, то новая средняя:
а) не изменится, так как число постоянно для всех вариант;
б) увеличится или уменьшится на это же число;
в) увеличится или уменьшится во столько же раз.
61. Если каждую варианту умножить или разделить на одно и то же постоянное число, то новая средняя:
а) не изменится, так как число постоянно для всех вариант;
б) увеличится или уменьшится на это же число;
в) увеличится или уменьшится во столько же раз.
62. Сумма отклонений вариант от средней всегда:
а) число положительное;
б) число отрицательное;
в) всегда не равна нулю;
г) всегда равна нулю.
63. Сумма квадратов отклонений вариант от средней всегда:
а) меньше, чем сумма квадратов отклонений от любого другого числа;
б) больше, чем сумма квадратов отклонений от любого другого числа;
в) может быть как больше, так и меньше;
г) всегда равна нулю.
64. К структурным средним относится:
а) мода; б) медиана; в) квартиль; г) дециль;
д) а, б; ж) в, г; з) а, б, в, г.
65. Модой называется:
а) варианта признака, наиболее часто встречающаяся в исследуемой совокупности;
б) значение изучаемого признака, которое занимает серединное место в ранжированном ряду единиц совокупности;
в) значение изучаемого признака, которое занимает серединное место в произвольно расположенном ряду единиц совокупности.
66. Медианной называется:
а) варианта признака, наиболее часто встречающаяся в исследуемой совокупности;
б) значение изучаемого признака, которое занимает серединное место в ранжированном ряду единиц совокупности;
в) значение изучаемого признака, которое занимает серединное место в произвольно расположенном ряду единиц совокупности.
67. Квартиль:
а) делит ранжированный ряд на две части;
б) на пять частей;
в) на четыре части;
г) на десять частей.
68. Дециль:
а) делит ранжированный ряд на две части;
б) на пять частей;
в) на четыре части;
г) на десять частей.
69. Для расчета моды в интервальном вариационном ряду применяют формулу:
а) 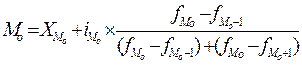 ; б)
; б) 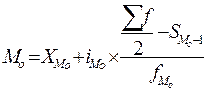 .
.
70. Для расчета медианны в интервальном вариационном ряду применяют формулу:
а) 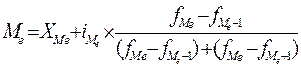 ; б)
; б) 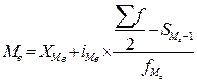 .
.
71. Какой показатель указывает наличие вариации в совокупности:
а) средняя арифметическая;
б) вариационная составляющая;
в) размах вариации;
г) медианна.
72. Общая сумма квадратов отклонений вариант от средней рассчитывается как:
а) 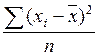 ; б)
; б) 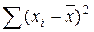 ; в)
; в) 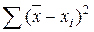 ; г)
; г) 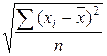 ;
;
д) а, г; е) б, в.
73. Дисперсия рассчитывается как:
а) 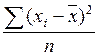 ; б)
; б) 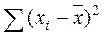 ; в)
; в) 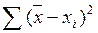 ; г)
; г) 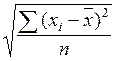 ;
;
д) а, г; е) б, в.
74. Среднее квадратическое отклонение рассчитывается как:
а) 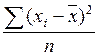 ; б)
; б) 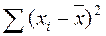 ; в)
; в) 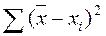 ; г)
; г) 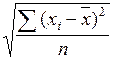 ;
;
д) а, г; е) б, в.
75. Средний квадрат отклонений по-другому называется:
а) стандартное отклонение;
б) дисперсия;
в) коэффициент вариации.
76. Среднее квадратическое отклонение измеряется в:
а) натуральных единицах;
б) относительных единицах;
в) натуральных единицах в квадрате.
77. Коэффициент вариации рассчитывается как отношение:
а) стандартного отклонения и моды;
б) среднего квадратического отклонения и среднего арифметического значения;
в) стандартного отклонения и медианы;
г) а, в; д) а, б, в.
78. Дисперсия постоянной величины:
а) всегда число положительное;
б) всегда число отрицательное;
в) может принимать и положительное и отрицательное значение;
г) всегда равняется нулю;
д) всегда равняется единице.
79. Если все варианты увеличить или уменьшить на одну и ту же величину (А), то дисперсия:
а) увеличится или уменьшиться на эту же величину;
б) не изменится;
в) увеличится или уменьшится во столько же раз;
г) увеличится или уменьшится в А2 раз.
80. Если все варианты умножить или разделить на одну и ту же величину (А), то дисперсия:
а) увеличится или уменьшиться на эту же величину;
б) не изменится;
в) увеличится или уменьшится во столько же раз;
г) увеличится или уменьшится в А2 раз.
81. Дисперсия всегда меньше среднего квадрата отклонения вариантов от произвольной величины на:
а) квадрат разности между средней арифметической и произвольной величиной;
б) сумму отклонений вариант от средней;
в) они равны.
82. Дисперсия алгебраической суммы независимых случайных величин равна:
а) сумме стандартных отклонений;
б) сумме квадратов отклонений;
в) сумме их дисперсий;
г) все ответы не верны.
83. Общая дисперсия рассчитывается как:
а) 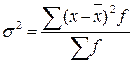 ; б)
; б) 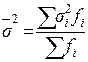 ; в)
; в) 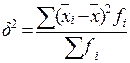 .
.
84. Внутригрупповая дисперсия рассчитывается как:
а) 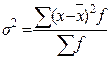 ; б)
; б) 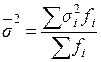 ; в)
; в) 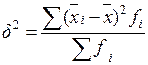
85. Межгрупповая дисперсия рассчитывается как:
а) 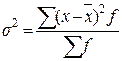 ; б)
; б) 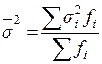 ; в)
; в) 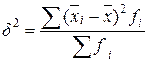 .
.
86. Вариация альтернативного признака рассчитывается как:
а) 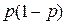 ; б)
; б) 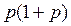 ; в)
; в) 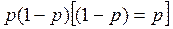 ;
;
г) а, б; д) б, в; е) а, в; ж) все ответы не верны.
87. В нормальном распределении коэффициент распределения равен:
а) единице;
б) нулю;
в) всегда положителен;
г) все ответы не верны.
88. Коэффициент асимметрии рассчитывается как:
а) 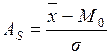 ; где
; где 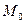 – мода; б)
– мода; б) 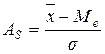 ; где
; где 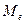 – медиана;
– медиана;
в) 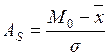 ; г)
; г) 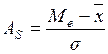 ; д) а, б; е) в, г.
; д) а, б; е) в, г.
89. Показатель эксцесса характеризует:
а) степень крутизны распределения;
б) степень округлости распределения;
в) полноту распределения.
90. Ряд динамики характеризует:
а) изменение размеров явления во времени;
б) распространение явления в пространстве;
в) сравнение одной единицы совокупности с базовой величиной.
г) а, б.
91. Параметры, характеризующие ряд динамики – это:
а) моменты времени или периоды, к которым относятся статистические данные;
б) непосредственно статистические данные;
в) а, б.
92. Уровнем ряда динамики называется:
а) момент времени или период, к которым относятся статистические данные;
б) непосредственно статистические данные, характеризующие размер явления в определенный момент времени;
в) а, б.
93. Ряды динамики подразделяются в зависимости от:
а) приводимых в них статистических показателей;
б) времени, отображаемого в динамическом ряду;
в) полноты времени отображаемого в динамическом ряду.
Г) а, б, в; д) все ответы не верны.
94. Моментный динамический ряд – это:
а) ряд, уровни которого отражают размеры изучаемого явления, за какой то промежуток времени;
б) ряд, уровни которого выражают величину явления на определенный, конкретный момент времени;
в) а, б; г) все ответы не верны.
95. Интервальный динамический ряд – это:
а) ряд, уровни которого отражают размеры изучаемого явления за какой-то промежуток времени;
б) ряд, уровни которого выражают величину явления на определенный, конкретный момент времени;
в) а, б; г) все ответы не верны.
96. Начальный уровень динамического ряда, как правило, обозначается как:
а) 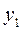 ; б)
; б) 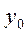 ; в) а, б;
; в) а, б;
97. Текущим уровнем динамического ряда называют:
а) сравниваемый уровень ряда динамики;
б) уровень, по отношению к которому проводится сравнение;
в) а, б;
98. Базисным уровнем динамического ряда называют:
а) сравниваемый уровень ряда динамики;
б) уровень, по отношению к которому проводится сравнение;
в) а, б;
99. Базисным уровнем может быть:
а) начальный уровень динамического ряда (либо любой другой, постоянно взятый за основу сравнения уровень);
б) уровень, предыдущий текущему уровню;
в) средний уровень;
г) а, б; д) а, в; е) а, б, в; ж) все ответы не верны.
100. Абсолютный прирост рассчитывается как:
а) отношение двух уровней;
б) разность двух уровней;
в) а, б;
101. Коэффициент роста рассчитывается как:
а) отношение двух уровней;
б) разность двух уровней;
в) а, б;
102. Коэффициент прироста рассчитывается как:
а) отношение абсолютного прироста к базисному уровню;
б) коэффициент роста минус 1;
в) а, б;
г) все ответы не верны.
103. Как темп роста (прироста) отличается от коэффициента роста (прироста):
а) это одно и то же;
б) темп – это коэффициент, умноженный на 100;
в) темп – это коэффициент, плюс 100;
г) а, б; д) а, в; е) а, б, в.
104. Абсолютное значение одного процента прироста показывает:
а) часть абсолютного прироста, которая обеспечила 1% относительного прироста;
б) часть относительного прироста, которая обеспечила 1% абсолютного прироста;
в) а, б;
105. Абсолютное значение одного процента рассчитывается как:
а) отношение двух уровней;
б) разность двух уровней;
в) отношение абсолютного прироста к темпу роста за тот же период;
г) как сотая часть предыдущего уровня;
д) а, б; е) в, г.
106. Средний уровень интервального ряда динамики с равными интервалами рассчитывается как:
а) средняя хронологическая;
б) средняя арифметическая взвешенная;
в) средняя арифметическая простая исходных уровней;
107. Средний абсолютный прирост рассчитывается как:
а) средняя арифметическая из показателей абсолютного прироста;
б) средняя арифметическая исходных уровней;
в) отношение суммы абсолютных приростов к числу уровней динамического ряда;
108. Средний коэффициент (темп) роста рассчитывается по формуле:
а) средней арифметической;
б) средней геометрической;
в) средней гармонической взвешенной;
109. Средний коэффициент (темп) прироста рассчитывается по формуле:
а) средней арифметической;
б средней гармонической взвешенной;
в) как средний коэффициент (темп) роста минус 1 (100);
110. Тренд динамического ряда – это:
а) наиболее часто встречающийся уровень динамического ряда;
б) основная тенденция изучаемого динамического ряда;
в) серединный уровень динамического ряда;
г) а), в).
111. Для выявления тренда в динамических рядах используют:
а) метод средних;
б) фазачастотный критерий знаков первой разрядности;
в) критерий Кокса и Стюарта;
г) метод серий;
д) а, б; е) а, в; ж) в, г; з) а, б, в, г.
112. К механическим методам выравнивания динамического ряда относится:
а) метод укрупнения интервалов;
б) метод скользящей средней;
в) выравнивание по параболе второго порядка:
г) выравнивание по прямой;
д) выравнивание по гиперболе;
е) а, б; ж) в, г, д.
113. При выравнивании динамического ряда методом средних скользящих выбирают:
а) четное количество периодов;
б) нечетное количество периодов;
в) а,б.
114. К аналитическому выравниванию динамического ряда относится:
а) метод укрупнения интервалов;
б) метод скользящей средней;
в) выравнивание по параболе второго порядка:
г) выравнивание по прямой;
д) выравнивание по гиперболе;
е) а, б; ж) в, г, д.
115. Оценку параметров уравнений 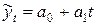 осуществляют при помощи:
осуществляют при помощи:
а) метода наименьших квадратов (МНК);
б) метода наименьших расстояний;
в)метода избранных точек;
г) б, в; д) а, б, в.
116. Оценку значимости уравнения выравнивания динамического ряда производят с помощью:
а) критерия Стюарта;
б) критерия Кокса;
в) критерия Фишера;
г) а, б, в.
117. При выравнивании динамического ряда по прямой МНК дает следующую систему уравнений:
а) 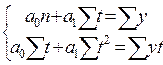 ; б)
; б) 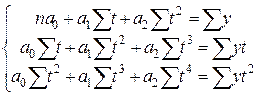 ; в)
; в) 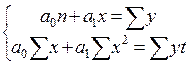 ; г)
; г) 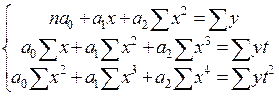 ;
;
д) а, б; е) в, г.
| <== предыдущая лекция | | | следующая лекция ==> |
| Недедуктивна (правдоподібна) аргументація | | | Із захистної промови Андрієвського щодо братів Келеш |