
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
ЗУСТРІЧНИЙ БІЙ
Дата добавления: 2015-10-12; просмотров: 745
|
|
В качестве основного признака изучается показатель общей заболеваемости (по обращаемости) по отдельным группам заболеваний в различных возрастных, социальных и профессиональных группах населения, административных территориях. При проведении выборочного изучения заболеваемости необходимо обеспечить условие репрезентативности выборки.
 На первом этапе расчета выборочной совокупности устанавливаются желательные пределы ошибки выборки
На первом этапе расчета выборочной совокупности устанавливаются желательные пределы ошибки выборки  и приблизительные характеристики распределения исследуемого показателя.
и приблизительные характеристики распределения исследуемого показателя.
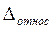 На практике задается не величина абсолютной ошибки , а величина относительной погрешности , выраженная в процентах.
На практике задается не величина абсолютной ошибки , а величина относительной погрешности , выраженная в процентах.


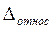 Далее определяется уравнение, связывающее число наблюдений n (объем выборки) с желательным уровнем точности ожидаемых результатов (надежности ) и величиной предельной ошибки выборки (или ).
Далее определяется уравнение, связывающее число наблюдений n (объем выборки) с желательным уровнем точности ожидаемых результатов (надежности ) и величиной предельной ошибки выборки (или ).
Объем выборочной совокупности n рассчитывается по следующему алгоритму:
1. 

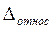

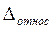 Исследователь сам выбирает желаемые значения относительной погреш-ности и надежности . Рекомендуемые значения: = 0,95, = 1%.
Исследователь сам выбирает желаемые значения относительной погреш-ности и надежности . Рекомендуемые значения: = 0,95, = 1%.
2. 
 Рассчитывается дисперсия генеральной совокупности . В реальных зада-чах, вместо , обычно используют исправленную выборочную дисперсию .
Рассчитывается дисперсия генеральной совокупности . В реальных зада-чах, вместо , обычно используют исправленную выборочную дисперсию .
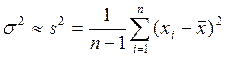
3. 




 При оценке доли изучаемого признака (заболеваемости) по относительной частоте (частости) появления в генеральной совокупности, рассчитывается величина дисперсии доли . Оценивать
При оценке доли изучаемого признака (заболеваемости) по относительной частоте (частости) появления в генеральной совокупности, рассчитывается величина дисперсии доли . Оценивать  (
(  )следует так, чтобы произведение принимало наибольшее значение. Если относительная частота даже приблизительно не известна, можно провести примерный расчет выборки, вводя в расчет максимальную величину дисперсии доли, равную 0,25 (т.е. при = 0,5). В случаях, когда заведомо меньше 0,5 значение можно уменьшить, и, тем самым уменьшится необходи-мый объем выборки.
)следует так, чтобы произведение принимало наибольшее значение. Если относительная частота даже приблизительно не известна, можно провести примерный расчет выборки, вводя в расчет максимальную величину дисперсии доли, равную 0,25 (т.е. при = 0,5). В случаях, когда заведомо меньше 0,5 значение можно уменьшить, и, тем самым уменьшится необходи-мый объем выборки.
4.  Определяются значения доверительного коэффициента t (по таблице распределения Стьюдента) при разных значениях и n.
Определяются значения доверительного коэффициента t (по таблице распределения Стьюдента) при разных значениях и n.
5. Рассчитываются значения оценки s:
· по пробной выборке объема n1 , меньшего предполагаемого;
· по данным предыдущих исследований;
· согласно каким-либо предположениям о структуре совокупности
6. Объем выборки для заданной надежности 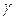 , гарантирующий определяемую заранее точность, определяется следующим образом:
, гарантирующий определяемую заранее точность, определяется следующим образом:

При достаточно больших N:
 .
.
7. Вычисление объема выборки n по частости  (при оценке доли определенного признака в изучаемой генеральной совокупности) проводится в соответствии с п.п.3, 4. В этом случае, выборочная дисперсия
(при оценке доли определенного признака в изучаемой генеральной совокупности) проводится в соответствии с п.п.3, 4. В этом случае, выборочная дисперсия  представлена выражением
представлена выражением  . Объем выборки n вычисляется по формуле:
. Объем выборки n вычисляется по формуле:
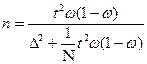 .
.
 |
При достаточно больших N (тогда ) формула выглядит следующим образом:

 .
.
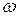
 При максимальной величине дисперсии доли равной =0,25 (т.е. при =0,5), при заданной величине предельной ошибки объем необходимой выборки находится по таблице 1:
При максимальной величине дисперсии доли равной =0,25 (т.е. при =0,5), при заданной величине предельной ошибки объем необходимой выборки находится по таблице 1:
Таблица 1.
Объем выборочной совокупности при максимально
возможной величине дисперсии.

|  , % , %
| |||||
| 1% | 2% | 2,5% | 5% | 7,5% | 10% | |
| 0,90 | ||||||
| 0,95 | ||||||
| 0,975 | ||||||
| 0,99 |
Пример:
Генеральная совокупность (1) – жители Новгородской области. Примем объем этой генеральной “совокупности n(1) = 700 000. Уровень охвата обязательным медицинским страхованием населения Новгородской области медицинской страховой организацией составляет 98%. Таким образом, объем генеральной совокупности будет n(2) = N(1) * 0.98 = 700000 * 0.98 = 686000.

 Расчет выборочной дисперсии по пробной выборке объема n1 , меньшего предполагаемого или по данным предыдущих исследований может быть затруднителен в виду отсутствия такой информации. Поэтому дальнейший расчет поведем по частости , характеризующей долю общей заболеваемости по обращаемости по данным государственной статистики.
Расчет выборочной дисперсии по пробной выборке объема n1 , меньшего предполагаемого или по данным предыдущих исследований может быть затруднителен в виду отсутствия такой информации. Поэтому дальнейший расчет поведем по частости , характеризующей долю общей заболеваемости по обращаемости по данным государственной статистики.
 В общем случае рассчитываем объем выборки, вводя максимальную величину дисперсии доли, равную 0,25.
В общем случае рассчитываем объем выборки, вводя максимальную величину дисперсии доли, равную 0,25.
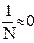
 Задаем величину предельной ошибки =1%, т.е. величина абсолютной предельной ошибки выборки будет = 0,01. Предполагая, что n>120 и задавая надежность
Задаем величину предельной ошибки =1%, т.е. величина абсолютной предельной ошибки выборки будет = 0,01. Предполагая, что n>120 и задавая надежность 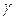 =0,95, получаем коэффициент доверия t =1,96 (табличная величина). Так как , то объем выборки n равен:
=0,95, получаем коэффициент доверия t =1,96 (табличная величина). Так как , то объем выборки n равен:


 С резервом выборки 5% , итоговый объем выборки будет равен 10850 единиц. При других значениях и , значения необходимого объема выборки представлены в таблице 1.
С резервом выборки 5% , итоговый объем выборки будет равен 10850 единиц. При других значениях и , значения необходимого объема выборки представлены в таблице 1.
В таблице 2 для некоторых объемов выборок при надёжности  представлены оценки точности
представлены оценки точности 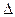 (предельной ошибки выборки).
(предельной ошибки выборки).
Таблица 2.
Оценка точности вычислений вероятности р при надёжности 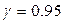
в зависимости от объёма выборки
| Значения оцениваемой вероятности р | ||||||||
| Объем выборки | 0.00 - 0.01 | 0.01- 0.02 | 0.02 - 0.05 | 0.05 - 0.10 | 0.10- 0.20 | 0.20- 0.30 | 0.30 - 0.40 | 0.40 - 0.50 |
| 0,000620 | 0,008677 | 0,013508 | 0,018594 | 0,024792 | 0,028403 | 0,030364 | 0,030990 | |
| 0,000438 | 0,006136 | 0,009552 | 0,013148 | 0,017531 | 0,020084 | 0,021471 | 0,021913 | |
| 0,000392 | 0,005488 | 0,008543 | 0,011760 | 0,015680 | 0,017964 | 0,019204 | 0,019600 | |
| 0,000277 | 0,003881 | 0,006041 | 0,008316 | 0,011087 | 0,012702 | 0,013579 | 0,013859 | |
| 0,000226 | 0,003168 | 0,004933 | 0,006790 | 0,009053 | 0,010371 | 0,011087 | 0,011316 | |
| 0,000196 | 0,002744 | 0,004272 | 0,005880 | 0,007840 | 0,008982 | 0,009602 | 0,009800 | |
| 0,000160 | 0,002240 | 0,003488 | 0,004801 | 0,006401 | 0,007334 | 0,007840 | 0,008002 | |
| 0,000139 | 0,001940 | 0,003021 | 0,004158 | 0,005544 | 0,006351 | 0,006790 | 0,006930 | |
| 0,000088 | 0,001227 | 0,001910 | 0,002630 | 0,003506 | 0,004017 | 0,004294 | 0,004383 | |
| 0,000062 | 0,000868 | 0,001351 | 0,001859 | 0,002479 | 0,002840 | 0,003036 | 0,003099 |
При оцениваемой вероятности  с надежностью 0,95 относительная частота
с надежностью 0,95 относительная частота 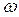 отличается от истинного (генерального) значения
отличается от истинного (генерального) значения  не более чем:
не более чем:
· на 0,018594 (т.е. 1,8594%) при объеме выборки 1000 наблюдений;
· на 0,013148 (т.е. 1,3148%) при объеме выборки 2000 наблюдений;
· на 0,008316 (т.е. 0,8316%) при объеме выборки 5000 наблюдений и т.д.
Фактические значения точности оценок вероятности окажутся заведомо меньше (лучше) приведенных, так как указанные в таблице 2 значения рассчитаны, исходя из верхней границы соответствующего интервала и генеральной совокупности бесконечного объема.
Существенное увеличение объема выборочной совокупности требует фактически пропорционального объема финансовых и материальных затрат, но при этом, как видим из приведенной таблицы, не приводит к радикальному увеличению точности оценок. Например, при  объем выборки 10000 гарантирует точность оценки
объем выборки 10000 гарантирует точность оценки  ; объем выборки 20000 гарантирует точность оценки
; объем выборки 20000 гарантирует точность оценки  ; объем выборки 100000 гарантирует точность оценки
; объем выборки 100000 гарантирует точность оценки  .
.
Основываясь на указанных в таблице значениях, рекомендуется не ставить самоцелью повышения точности оценок за счет неоправданного увеличения объема выборки, а найти разумный компромисс между приемлемой точностью и объемом выборочной совокупности (в исследовании, проводимом в Новгородской области, объем выборки равен 10000 наблюдений).
Для обеспечения качества выборочной совокупности в данной методике используются методы серийного, многоступенчатого и случайного (механического) отбора, при этом отбор респондентов в выборку проводится по следующему алгоритму:
1. Производится экономико-географическое зонирование территории (север, юг, запад, восток). С учетом географического расположения и характера региональных транспортных сетей (основные железнодорожные и автотранспортные магистрали), выделяются условно близкие по площади географические зоны с равным количеством муниципальных районов.
2. Внутри каждой зоны проводится отбор одного района, который характеризуется наиболее близкими (к средним в своей зоне) значениями следующих показателей государственной статистики:
· численность сельского населения;
· средняя плотность сельского населения;
· коэффициент, выражающий соотношение численности групп населения, занятых в индустриальном и аграрном секторах экономики.
3. Проводится внутрирайонная выборка поселений, являющихся основными базами для организации выборочного исследования.
4. В отобранных поселениях, на основе реестров застрахованных уточняются данные о населении. Лица, попавшие в выборку, должны быть идентифицированы по БД заболеваемости медицинских страховых организаций.
Для формирования выборочной совокупности, объема n, из списка населения региона (БД “Реестр застрахованных” СМО или ТО ФОМС, либо любая другая БД, содержащая региональный список населения) с помощью компьютерных методик (генератор случайных чисел) формируется выборочная персонифицированная БД. Кроме того, формируется “резервная выборка” (резервная выборочная персонифицированная БД) с использованием тех же алгоритмов. В случае отсутствия индивидуума по месту прописки, отказа индивидуума от прохождения медосмотра и т.п., из этой резервной выборки отбираются индивидуумы взамен выбывшего (из той же половозрастной группы), т.е. производится “ремонт” выборки.
Сформированная таким образом выборочная совокупность репрезентативна в отношении всего населения региона. Полученная выборка (в виде персонифицированной базы данных) используется для проведения медицинских осмотров и изучения физического состояния населения, для проведения социологического мониторинга.
| <== предыдущая лекция | | | следующая лекция ==> |
| Наступ у лісі | | | В ТАКТИЧНОМУ ПОВІТРЯНОМУ ДЕСАНТІ |