Передмова

Дата добавления: 2015-10-18; просмотров: 548

Системы с переменной структурой (СПС) – это специальный класс нелинейных систем, в которых происходит переключение регуляторов (или их параметров) по сигналам блока изменения структуры (БИС) в зависимости от значений переменных состояния объекта [5].

Обычно каждый из регуляторов (образующий вместе с объектом соответст­вующую «структуру») является линейным, но благодаря переключению структур за­кон управления получается существенно нелинейным. Как правило, СПС состоит из двух линейных регуляторов и блока изменения структуры, работающего по релей­ному закону. Структурная схема такой системы приведена на рис. 1, гдеP₁, P₂ – линейные регуляторы; g(t) – задающее воздействие; y(t) – выход объекта; u(t)– управляющее воздействие; БИС– блок изменения структуры;ОУ – объект управления;ИУ– исполнительное устройство.

Переключение структур в СПС осуществляется для повышения качества процессов управления и упрощения синтеза регулятора.

В качестве примера СПС можно рассмотреть систему, у которой каждая из линейных структур является гармоническим осциллятором (консервативным звеном), но с разными параметрами собственных колебаний, а благодаря переключению структуры получается устойчивая система с малым временем переходного процесса.

Линиями переключения в данном примере являются оси координат. Уравнения линий переключения: x = 0 и .

Другой пример СПС – система с переменным демпфированием [5], в которой коэффициент обратной связи по производной в законе управления переключается в зависимости от рассогласования. В результате удается добиться малого времени переходного процесса при незначительном перерегулировании.

Рассмотрим работу СПС более подробно. Пусть в фазовом пространстве (пространстве состояний) системы имеется некоторая поверхность (поверхность переключения), заданная уравнением S(x) = 0, где x=x(t) – вектор состояния системы. Эта поверхность делит пространство состояний на области, где 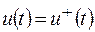и . Так как при переключении u(t) обычно меняется скачком, поверхность S(x)=0 называется также поверхностью разрыва [13]. При переходе изображающей точки через поверхность S(x) = 0 возможны следующие случаи: 1) вектор фазовой скорости направлен в область, смежную с исходной (рис. 3, а); 2) вектор фазовой скорости направлен вдоль поверхности разрыва (рис. 3, б); 3) вектор фазовой скорости после переключения направлен в исходную область (рис. 3, в).

Случай 1 имеет место в рассмотренных выше примерах СПС. В случае 2 фазовая траектория, соответствующая управлению , лежит на поверхности S(x)=0. Это явление характерно для оптимальных по быстродействию систем управления [7,8], однако оно практически недостижимо из-за погрешностей в реализации. Случай 3 отличается от случаев 1 и 2 тем, что здесь в процессе движения моменты переключения не изолированы друг от друга. Теоретически переключение структур наступает в сколь угодно близкие между собой моменты времени. Изображающая точка, попав на поверхность разрыва, должна на ней остаться, так как вектор фазовой скорости всегда направлен в сторону этой поверхности. Такой вид движения системы называется идеальным скользящим режимом [3,5,13].

На практике из-за неидеальности элементов и дополнительных инерционностей в системе возникает движение с относительно высокой частотой и малой амплиту­дой относительно поверхности разрыва – так называемый реальный скользящий режим [13].

Рассмотрим поведение системы в идеальном скользящем режиме. Будем предполагать, что указанными факторами можно пренебречь и движение происходит непосредственно по поверхности переключения, а не в ее пограничном слое.

При теоретическом изучении скользящих режимов имеются определенные сложности, связанные с невыполнением условий теоремы существования и единственности решений дифференциальных уравнений. Дело в том, что правые части уравнений, описывающих процесс в СПС, претерпевают разрыв при переключении структур. Кроме того, как показано выше, в скользящем режиме изображающая точка находится на поверхности разрыва в каждый момент времени. Поэтому требуется доопределить уравнения системы таким образом, чтобы получить решение, описывающее движение по поверхности переключения, но без разрывов правых частей уравнения. Эта задача не может быть решена однозначно. Известно несколько способов такого доопределения. Воспользуемся методом эквивалентного управления, предложенным В.И. Уткиным [13].

Пусть объект управления описывается системой уравнений

, (1)

где x(t) – вектор состояния объекта, u(t) – управляющее воздействие.

Регулятор описывается зависимостью

u =φ(x), (2)

причем функция φ(x) претерпевает разрыв на поверхности переключения, которая задается уравнением

S(x) = 0. (3)

Это означает, что при S(x) > 0 и при S(x) < 0 а значение φ⁰(x) при S(x) = 0 не определено.

Задача состоит в определении φ⁰(x) таким образом, чтобы полученное непрерывное управление соответствовало движению системы по поверхности (3). Так как при таком движении S(x) = 0, то производная по времени функции S(x), вычисленная в силу системы (1), тождественно равна нулю, то есть

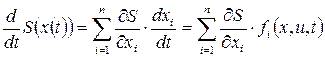= 0. (4)

Из полученного соотношения (4) выразим эквивалентное управление 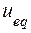. Далее подставляется в (1) и находится X(t) из совместного решения уравнений

, S(x) = 0.

Эквивалентное управление имеет определенный физический смысл. Если рассмотреть движение системы (1), (2) в реальном скользящем режиме, то управление u(t) будет содержать колебания с высокой частотой. Если сигнал u(t) пропустить через фильтр с соответствующей постоянной времени, то можно выделить низкочастотную, или «среднюю», составляющую, которая и будет соответствовать [13].

В лабораторной работе рассматривается СПС, объект управления которой описывается системой уравнений

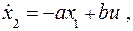(5)

где a, b – параметры объекта, а управление u(t) обеспечивает попадание на поверхность разрыва вида (3) и движение по ней в скользящем режиме. Очевидно, для рассматриваемого объекта фазовое пространство представляет собой плоскость 0x₁x₂. Уравнение (3) будем рассматривать в виде S(x) =τx₂ + x₁, где τ – заданный параметр. Таким образом, поверхность разрыва в нашем случае – прямая на плоскости 0x₁x₂.

В соответствии с изложенным выше методом найдем Имеем S(x(t)) = τx₂ + x₁, , откуда в силу (5)

. (6)

Полагая , найдем :

. (7)

Подставив (7) в (5), получим систему уравнений, описывающих движение объекта в скользящем режиме:

(8)

Уравнения (8) следует решать с учетом условия S(x) = τx₂ + x₁ = 0, откуда x₁ = –τx₂. Окончательное решение имеет вид

, . (9)

Если задано x₁(0), нетрудно найти Отметим, что за начало отсчета времени здесь принят момент t^* возникновения скользящего режима.

Таким образом, при движении по линии переключения мы получим процесс, соответствующий переходному процессу для апериодического звена первого порядка с постоянной времени τ. Отметим проявившуюся в рассмотренном примере важную особенность поведения СПС в скользящем режиме: характеристики процесса не зависят от параметров a и b объекта управления, а определяются видом линии переключения (параметром τ). Это свойство позволяет использовать СПС для обеспечения параметрической инвариантности САУ.

Выше было принято, что система находится в скользящем режиме. Попадание на поверхность разрыва и движение по ней обеспечивается соответствующим выбором управления. В нашем примере управляющее воздействие можно сформировать в виде

u(t) = –k₁x₁(t) – k₂x₂(t),

где k₁ и k₂ – коэффициенты регулятора, значения которых изменяются блоком изменения структуры.

Рассмотрим случай a<0 (объект статически неустойчив). Положим k₂=0, а значение k₁ выберем таким образом, чтобы одна из полученных структур была неустойчивой, а другая – колебательной. В первом случае достаточно положить k₁=0, а во втором . Фазовые портреты для каждой из структур приведены на рис. 4.

Организуем переключение коэффициента k₁ по прямым S(x)=τx₂ +x₁=0 и x₁ = 0, то есть реализуем закон управления следующим образом:

, (10)

где , S(x) = τx₂ + x₁.

Нетрудно убедиться, что при надлежащем выборе τ возможны два варианта расположения линии переключения S(x) = 0 относительно асимптоты гипербол (рис. 5). При τ>1 в системе возникает скользящий режим по прямой τx₂ +x₁ =0 (рис. 5, а), при τ<1 получаем фазовый портрет, изображенный на рис. 5, б. Скользящий режим в этом случае не возникает и система лишена рассмотренных выше положительных свойств.

Отметим, что на прямой x₁ = 0 также происходит переключение структур, но она не является линией разрыва, так как в соответствии с (10) здесь .

Сопоставление случаев, показанных на рис. 5, а, б, показывает, что параметры объекта (определяющие положение линии ) влияют на выбор τ, и, следовательно, в соответствии с (9), ограничивают достижимое быстродействие СПС с регулятором (10).