
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Тема 11. Облік нематеріальних активів
Дата добавления: 2015-10-18; просмотров: 798
|
|
1. Уравнения OУ, закон управления и схема набора СПС.
2. Фазовые портреты и графики временных процессов для рассмотренных вариантов структуры системы.
Литература
1. Андриевский А.Б., Андриевский Б.Р., Фрадков А.Л. Использование системы Scilab. Практическое пособие. - СПб: БГТУ, 2008 (электронный ресурс).
2. Андриевский Б.Р. Анализ систем в пространстве состояний. СПб.: ИПМаш РАН, 1997.
3. Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления с примерами на языке Matlab. СПб.: Наука, 1999.
4. Андриевский Б.Р., Фрадков А.Л. Элементы математического моделирования в программных средах Matlab 5 и Scilab. СПб.: Наука, 2001.
5. Бесекерский В.А.Попов Е.П. Теория систем автоматического управления. СПб: Профессия, изд. 4, 2003.
6. Динамика систем управления ракет с бортовыми цифровыми вычислительными машинами/ Под ред. М. С. Хитрика и С. М. Федорова. М.: Машиностроение, 1976.
7. Иванов В.А., Фалдин Н.В. Теория оптимальных систем автоматического управления. М.: Наука, 1981.
8. Козлов Ю.М. Методы непрерывной оптимизации систем управления летательными аппаратами. Л.: ЛМИ, 1981.
9. Методы исследования нелинейных систем автоматического управления /Под ред. Р.А.Нелепина. М.: Наука, 1975.
10. Первозванский А.А. Курс теории автоматического управления. М.: Наука, 1986.
11. Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. М.: Наука, 1979.
12. Справочник по теории автоматического управления /Под ред. А.А.Кра-совского. M.: Наука, 1987.
13. Уткин В.И. Скользящие режимы в задачах оптимизации и управления. М.: Наука, 1981.
СОДЕРЖАНИЕ
| Лабораторная работа № 1. Исследование основных методов повышения точности систем автоматического управления . . . . . . . | |
| Лабораторная работа № 2. Исследование САУ с дискретной коррекцией | |
| Лабораторная работа № 3. Исследование автоколебаний в нелинейной системе . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Лабораторная работа 4. Исследование устойчивости нелинейной САУ с неединственным соcтоянием равновесия . . . . . . . . . . . | |
| Лабораторная работа № 5. Исследование системы с переменной структурой . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Литература |
Им. Д. Ф. УСТИНОВА
Кафедра «Системы обработки информации и управления»
Б.Р. АНДРИЕВСКИЙ, В. Ю. ЕМЕЛЬЯНОВ, Б. Ф. КОРОТКОВ
ТЕОРИЯ УПРАВЛЕНИЯ
Лабораторный практикум
В среде Scilab
Санкт-Петербург
УДК 681.51
Теория управления:Лабораторный практикум в среде Scilab / Б.Р. Андриевский, В. Ю. Емельянов, Б.Ф. Коротков; Балт. гос. техн. ун-т; СПб., 2010. 45 с.
Посвящен вопросам синтеза линейных непрерывных и дискретных систем, анализу нелинейных систем и систем с переменной структурой.
Содержит основные сведения из теории, описание используемых моделей, руководство по выполнению работ на персональном компьютере в программной среде Scilab/Scicos с вариантами индивидуальных заданий, перечень рекомендуемой литературы.
Предназначен для студентов специальностей 160403, 230102, 230201.
Ил. 19. Табл. 7.
Рецензент
Утверждено
редакционно-издательским
советом университета
Ó БГТУ, СПб, 2010
Лабораторная работа № 1
ИССЛЕДОВАНИЕ ОСНОВНЫХ МЕТОДОВ ПОВЫШЕНИЯ
ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Цель работы – сравнительный анализ различных методов повышения точности САУ.
Основные сведения из теории
К числу важнейших показателей качества систем автоматического управления (САУ) относится установившаяся (статическая) ошибка – величина ошибки управления x(t)=g(t)–y(t) в установившемся процессе. Здесь g(t) – задающее воздействие, y(t) – выход системы.
Установившаяся ошибка САУ может быть измерена по окончании переходного процесса или рассчитана. Для линейной системы при известных структуре, параметрах и задающем воздействии используется теорема о конечном значении:
 ,
,
где Фx(s) – передаточная функция замкнутой системы по ошибке, G(s) – изображение по Лапласу задающего воздействия.
При одновременном действии на систему нескольких сигналов используется принцип суперпозиции:
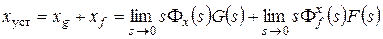 , (1)
, (1)
где xg, xf – составляющие статической ошибки, определяемые задающим и возмущающим воздействиями;  – передаточная функция замкнутой системы по ошибке от возмущающего воздействия; F(s) – изображение по Лапласу возмущающего воздействия f(t).
– передаточная функция замкнутой системы по ошибке от возмущающего воздействия; F(s) – изображение по Лапласу возмущающего воздействия f(t).
Если главная обратная связь в системе единичная и отрицательная, соотношение (1) принимает вид
 , (2)
, (2)
где W(s) – передаточная функция разомкнутой системы, Wf (s) – передаточная функция разомкнутой системы по возмущающему воздействию.
Если система является статической как по задающему, так и по возмущающему воздействиям, то при g(t)=g01(t)и f(t)=f01(t) формула (2) позволяет получить
 , (3)
, (3)
где K – общий коэффициент усиления по разомкнутой цепи, kf – коэффициент передачи от точки приложения возмущения f(t) до выхода системы y(t).
Из выражения (3) следует, что величина ошибки статической системы может быть уменьшена при увеличении общего коэффициента усиления. Однако это увеличение связано с уменьшением запаса устойчивости системы. Поэтому одновременно с увеличением коэффициента K необходимо вводить в САУ корректирующие (демпфирующие) средства.
Разработаны и другие методы повышения точности:
1) повышение порядка астатизма, что соответствует введению в систему интегрирующих или изодромных звеньев;
2) введение производной от ошибки в закон управления;
3) введение неединичных обратных связей;
4) применение комбинированного управления.
1.1. Описание исследуемой системы
В работе исследуется система управления, структурная схема которой изображена на рис.1. Нескорректированная система состоит из трех последовательно включенных апериодических звеньев. К системе приложено задающее воздействие g(t)=g0×1(t), на объект управления также действует возмущающее воздействие f(t)=f0×1(t).
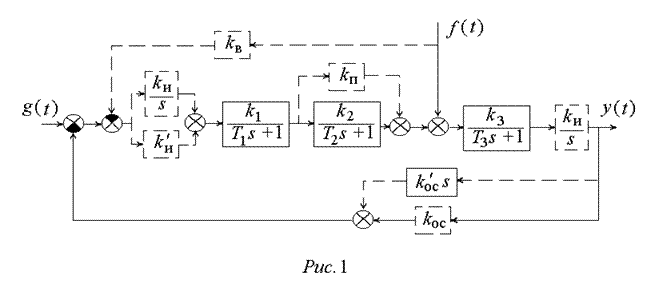 |
На структурной схеме пунктиром показаны дополнительные звенья, которые вводятся в систему с целью повышения ее точности:
1) прямое параллельное корректирующее устройство с коэффициентом передачи kп, позволяющее ввести производную от ошибки в закон управления;
2) вспомогательное дифференцирующее звено с коэффициентом передачи k'ос, позволяющее реализовать гибкую обратную связь;
3) интегрирующее звено с коэффициентом передачи kи, позволяющее повысить порядок астатизма системы;
4) изодромное звено с коэффициентами передачи kи и k'и, позволяющее повысить порядок астатизма системы без существенной потери запаса устойчивости;
5) вспомогательное звено с коэффициентом передачи kос, позволяющее реализовать цепь основной обратной связи с коэффициентом передачи, отличным от единицы;
6) дополнительное звено с коэффициентом передачи kв, позволяющее вводить на вход системы сигнал, пропорциональный возмущению f(t), с целью компенсации последнего, и тем самым создать комбинированную систему управления.
1.2. Нескорректированная система
Исходная система является статической и состоит из трех последовательных апериодических звеньев, охваченных единичной обратной связью (kос=1). Передаточная функция разомкнутой системы
 ,
,
где K0=k1k2k3 – общий коэффициент усиления.
Нетрудно убедиться, что исходная САУ является статической как по задающему, так и по возмущающему воздействиям, и для нее справедливо соотношение (3). Оценим возможность повышения точности нескорректированной системы путем увеличения коэффициента K0.
Основная передаточная функция нескорректированной замкнутой системы:
 . (4)
. (4)
Характеристический полином нескорректированной замкнутой системы:
 .
.
Используя критерий устойчивости Гурвица, можно определить условия устойчивости замкнутой САУ и критическое значение коэффициента K0, при котором нескорректированная САУ будет находиться на колебательной границе устойчивости.
В случае характеристического полинома третьей степени для анализа устойчивости достаточно рассмотреть определитель второго порядка:
 .
.
Условием устойчивости является неравенство Δ2>0, откуда
K0<K0кр, где 
Поэтому возможность повышения точности исследуемой САУ лишь за счет увеличения коэффициента усиления разомкнутой системы ограничена, причем максимально допустимое значение K0 должно быть меньше K0кр в соответствии с требуемым запасом устойчивости системы.
| <== предыдущая лекция | | | следующая лекция ==> |
| Тема 7. Оцінювання і калькуляція в системі бухгалтерського обліку | | | Тема 15. Облік власного капіталу |