
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Тема 15. Облік власного капіталу
Дата добавления: 2015-10-18; просмотров: 624
|
|
Введение производной от ошибки в закон управления может быть осуществлено за счет использования прямой параллельной корректирующей цепи с коэффициентом передачи kп.
Передаточная функция разомкнутой скорректированной системы в этом случае будет иметь вид
 ,
,
где K=k1(k2+kп)k3 – общий коэффициент усиления;  – постоянная времени, определяющая уровень сигнала управления по производной.
– постоянная времени, определяющая уровень сигнала управления по производной.
Используя соотношение (2) или структурный признак астатизма [5], нетрудно убедиться, что система осталась статической как по задающему, так и по возмущающему воздействиям.
Характеристический полином замкнутой скорректированной системы имеет вид
 .
.
Отсюда получаем условие для определения критического значения коэффициента усиления:
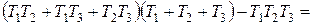
 ,
,

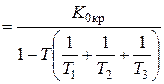 . (5)
. (5)
Из формулы (5) видно, что, вводя производную в закон управления, можно значительно расширить границу увеличения коэффициента усиления и, следовательно, уменьшить обе составляющие ошибки.
1.4. Введение гибкой обратной связи
При добавлении в цепь единичной обратной связи системы дополнительного дифференцирующего звена с коэффициентом k'ос (см. рис.1) передаточная функция обратной связи примет вид
 .
.
В этом случае соответствующие передаточные функции замкнутой системы определяются по соотношениям
 ,
,  ,
,  . (6)
. (6)
На основе (6) получим характеристический полином замкнутой системы:
 .
.
K0кр определяется аналогично предыдущему подразделу.
1.5. Повышение порядка астатизма
При введении дополнительного идеального интегрирующего звена (см. рис.1) повышается порядок астатизма системы. Передаточная функция разомкнутой системы принимает вид
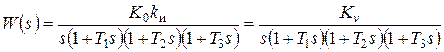 , (7)
, (7)
где Kv = K0kи – новый коэффициент усиления разомкнутой системы, в рассматриваемом случае называемый добротностью по скорости [5] и приобретающий размерность с–1. Ошибка системы в установившемся режиме работы может быть определена на основе (2):
 . (8)
. (8)
Из формулы (8) следует, что скорректированная САУ стала астатической по задающему воздействию и осталась статической по отношению к возмущающему воздействию. Кроме того, из этой формулы следует, что при введении интеграла составляющая ошибки xf может возрасти, так как при введении интеграла обычно уменьшается запас устойчивости системы, что приводит к необходимости снижения коэффициента усиления.
На основе критерия Гурвица с учетом повышения степени характеристического полинома можно найти условие устойчивости для данной структурной схемы САУ:
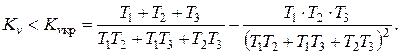 (9)
(9)
Нетрудно убедиться, что здесь критическое значение коэффициента усиления значительно меньше, чем при отсутствии интегрирующего звена.
Более эффективным является включение интегрирующего звена в состав регулятора (интегральный закон управления). Если в отличие от рис. 1 переместить интегратор до точки приложения возмущающего воздействия, передаточная функция (7) и условие (9) сохранятся, но на основе (2) можно убедиться в достижении теперь астатизма как по задающему, так и по возмущающему воздействиям. При воздействиях рассматриваемого вида необходимость снижения коэффициента усиления не повлияет на точность системы в установившемся режиме.
1.6. Повышение порядка астатизма введением изодромного звена
Повысить порядок астатизма системы можно также путем введения в прямую цепь изодромного звена (пропорционально-интегрального регулятора) с передаточной функцией (см. рис.1)
 .
.
Передаточная функция разомкнутой системы принимает вид
 ,
,
где Kv = K0kи – новый коэффициент усиления разомкнутой системы (добротность);  – новая постоянная времени.
– новая постоянная времени.
Получить условие устойчивости для данной структуры САУ и убедиться, что значение критического коэффициента усиления здесь выше, чем при введении в систему идеального интегратора, предлагается самостоятельно. Здесь может быть полезно также использование частотного критерия устойчивости Найквиста.
Отметим, что от места включения в систему изодромного звена зависит достижение астатизма по всем или части воздействий, что полностью аналогично результатам предыдущего пункта.
1.7. Введение неединичной обратной связи
В данной работе неединичная обратная связь реализуется путем введения в цепь главной обратной связи дополнительного звена с коэффициентом передачи koc(см. рис.1).
В этом случае передаточная функция замкнутой системы автоматического управления определяется следующим образом:
 .
.
Для получения полной инвариантности САУ по отношению к задающему воздействию необходимо выполнение условия Ф(s)=1, откуда следует требуемая передаточная функция главной обратной связи:
 .
.
Реализация частичной инвариантности (обеспечение астатизма первого порядка относительно задающего воздействия) достигается жесткой обратной связью с коэффициентом передачи:
 . (10)
. (10)
Если возмущающее воздействие f(t) будет приложено к САУ, то установившееся значение ошибки определяется лишь составляющей xf , вызванной возмущающим воздействием.
Из вышеизложенного следует, что введение неединичной обратной связи позволяет обеспечить астатизм по задающему воздействию для исходной статической САУ.
1.8. Комбинированное регулирование
Использование рассмотренных выше методов повышения точности САУ вызывает общие трудности, связанные с обеспечением устойчивости системы и надлежащего качества переходных процессов.
Поэтому при решении задачи повышения точности САУ иногда целесообразно отойти от чистого принципа управления по отклонению (или по интегралам и производным от него) и соединить этот принцип с другим – с управлением по возмущающему или задающему воздействию. Такого рода системы управления называются комбинированными. В подобных системах управление осуществляется по замкнутому и разомкнутому контурам.
В данной лабораторной работе исследуется введение дополнительного управления по возмущению (см. рис.1). В соответствии со структурной схемой составляющая ошибки от возмущения может быть найдена из следующей системы уравнений в изображениях:

 ,
,  .
.
Пусть g(t)=0 , тогда X(s) = –Y(s). Составляющая ошибки от возмущения определяется выражением
 .
.
Отметим, что характеристический полином комбинированнной системы остается без изменений, следовательно, введение управления по возмущению не влияет на устойчивость.
Установившаяся ошибка от возмущающего воздействия
 .
.
При выполнении условия
kвk1k2 = 1 (11)
установившаяся ошибка обращается в ноль, то есть в системе достигается частичная инвариантность по отношению к возмущающему воздействию (система приобретает астатизм первого порядка). Рассмотренный прием по существу обеспечивает компенсацию ступенчатого возмущающего воздействия.
| <== предыдущая лекция | | | следующая лекция ==> |
| Тема 11. Облік нематеріальних активів | | | Теми рефератів |