Вращение твердого тела
Для кинематического описания вращения твердого тела удобно использовать угловые величины: угловое перемещение Δ φ, угловую скорость ω
и угловое ускорение ε
В этих формулах углы выражаются в радианах. При вращении твердого тела относительно неподвижной оси все его точки движутся с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями. За положительное направление вращения обычно принимают направление против часовой стрелки.
При малых угловых перемещениях Δ φ модуль вектора
где r – модуль радиус-вектора
и между модулями линейного и углового ускорения:
Векторы
Разобьем вращающееся тело на малые элементы Δ m i. Расстояния до оси вращения обозначим через r i, модули линейных скоростей – через υ i. Тогда кинетическую энергию вращающегося тела можно записать в виде:
Физическая величина
В пределе при Δ m → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в СИ – килограмм-метр в квадрате (кг∙ м2). Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде
Эта формула очень похожа на выражение для кинетической энергии поступательно движущегося тела Момент инерции в динамике вращательного движения играет ту же роль, что и масса тела в динамике поступательного движения. Но есть и принципиальная разница. Если масса – внутреннее свойство данного тела, не зависящее от его движения, то момент инерции тела зависит от того, вокруг какой оси оно вращается. Для разных осей вращения моменты инерции одного и того же тела различны. Во многих задачах рассматривается случай, когда ось вращения твердого тела проходит через его центр массы. Положение x C, y C центра масс для простого случая системы из двух частиц с массами m 1 и m 2, расположенными в плоскости XY в точках с координатами x 1, y 1 и x 2, y 2 (рис. 1.23.2), определяется выражениями:
В векторной форме это соотношение принимает вид:
Аналогично, для системы из многих частиц радиус-вектор
Для сплошного тела суммы в выражении для
Равнодействующая сил тяжести в однородном поле тяготения приложена к центру масс тела. Если тело подвешено за центр масс, то оно находится в безразличном состоянии равновесия (см. §1.14). Любое движение твердого тела можно представить как сумму двух движений: поступательного движения со скоростью центра масс тела и вращения относительно оси, проходящей через центр масс. Примером может служить колесо, которое катится без проскальзывания по горизонтальной поверхности (рис. 1.23.4). При качении колеса все его точки движутся в плоскостях, параллельных плоскости рисунка. Такое движение называется плоским. При плоском движении кинетическая энергия движущегося твердого тела равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, проходящей через центр масс тела и перпендикулярной плоскостям, в которых движутся все точки тела:
где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.
В механике доказывается теорема о движении центра масс: под действием внешних сил центр масс любого тела или системы взаимодействующих тел движется как материальная точка, в которой сосредоточена вся масса системы. Иллюстрацией этого утверждения может служить рис. 1.23.5, на котором изображено движение тела под действием силы тяжести. Центр масс тела движется по параболической траектории как материальная точка, в то время как все другие точки движутся по более сложным траекториям.
Если твердое тело вращается относительно некоторой неподвижной оси, то его момент инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.
Рассмотрим сечение твердого тела произвольной формы, изображенное на рис. 1.23.6. Выберем координатную систему XY с началом координат O в центре масс C тела. Пусть одна из осей вращения проходит через центр масс C, а другая через произвольную точку P, расположенную на расстоянии d от начала координат. Обе оси перпендикулярны плоскости чертежа. Пусть Δ m i – некоторый малый элемент массы твердого тела. По определению момента инерции:
Выражение для I P можно переписать в виде:
Поскольку начало координат совпадает с центром масс C, последние два члена обращаются в нуль. Это следует из определения центра масс. Следовательно,
где m – полная масса тела. Этот результат называют теоремой Штейнера (теоремой о параллельном переносе оси вращения). На рис. 1.23.7 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
Второй закон Ньютона может быть обобщен на случай вращения твердого тела относительно неподвижной оси. На рис. 1.23.8 изображено некоторое твердое тело, вращающееся относительно оси, перпендикулярной плоскости рисунка и проходящей через точку O. Выделим произвольный малый элемент массы Δ m i. На него действуют внешние и внутренние силы. Равнодействующая всех сил есть
Касательная составляющая
где Если обе части написанного выше уравнения умножить на r i, то мы получим:
Здесь l i – плечо силы Теперь нужно аналогичные соотношения записать для всех элементов массы Δ m i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:
Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.
Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M. В итоге:
Это и есть основное уравнение динамики вращательного движения твердого тела. Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими. Обычно за положительное направление вращения принимают направление против часовой стрелки. Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины При изучении поступательного движения тел вводится понятие импульса тела Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L:
Поскольку
Окончательно будем иметь:
Это уравнение, полученное здесь для случая, когда I = const, справедливо и в общем случае, когда момент инерции тела изменяется в процессе движения. Если суммарный момент М внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется:
Следовательно,
Это и есть закон сохранения момента импульса. Иллюстрацией этого закона может служить неупругое вращательное столкновение двух дисков, насажанных на общую ось (рис. 1.23.9).
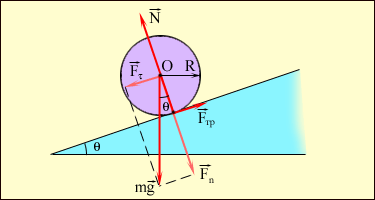
Закон сохранения момента импульса справедлив для любой замкнутой системы тел. Он выполняется, например, при движении планет по эллиптическим орбитам вокруг Солнца (второй закон Кеплера – см. §1.24). Уравнение вращательного движения тела можно записывать не только относительно неподвижной или равномерно движущейся оси, но и относительно оси, движущейся с ускорением. Основное уравнение динамики вращательного движения не изменяет своего вида и в случае ускоренно движущихся осей при условии, что ось вращения проходит через центр массы тела и что ее направление в пространстве остается неизменным. Примером может служить качение тела (обруч, цилиндр, шар) по наклонной плоскости с трением (рис. 1.23.10).
Ось вращения O проходит через центр масс тела. Моменты силы тяжести Уравнение вращательного движения:
где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, I C – момент инерции относительно оси O, проходящей через центр масс. Второй закон Ньютона для поступательного движения центра масс записывается в виде:
Исключая из этих уравнений F тр, получим окончательно:
Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара
|

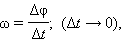

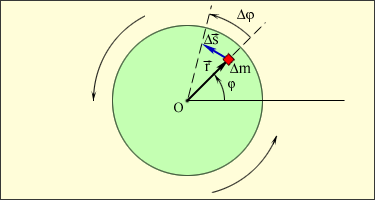
 линейного перемещения некоторого элемента массы Δ m вращающегося твердого тела выражается соотношением:
линейного перемещения некоторого элемента массы Δ m вращающегося твердого тела выражается соотношением: (рис. 1.23.1). Отсюда следует связь между модулями линейной и угловой скоростей:
(рис. 1.23.1). Отсюда следует связь между модулями линейной и угловой скоростей: и
и  направлены по касательной к окружности радиуса r. Следует вспомнить, что при движении тела по окружности возникает также нормальное или центростремительное ускорение, модуль которого есть
направлены по касательной к окружности радиуса r. Следует вспомнить, что при движении тела по окружности возникает также нормальное или центростремительное ускорение, модуль которого есть

 зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:
зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:

 только теперь вместо массы m в формулу входит момент инерции I, а вместо линейной скорости υ – угловая скорость ω.
только теперь вместо массы m в формулу входит момент инерции I, а вместо линейной скорости υ – угловая скорость ω.


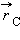 центра масс определяется выражением
центра масс определяется выражением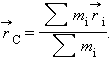



 и вращения (2) с угловой скоростью
и вращения (2) с угловой скоростью  относительно оси O, проходящей через центр масс.
относительно оси O, проходящей через центр масс.






 Ее можно разложить на две составляющие: касательную составляющую
Ее можно разложить на две составляющие: касательную составляющую  и радиальную
и радиальную  Радиальная составляющая создает центростремительное ускорение a n.
Радиальная составляющая создает центростремительное ускорение a n.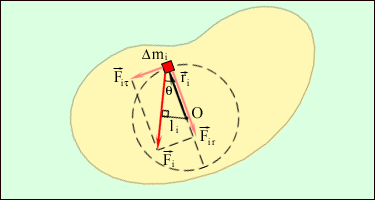
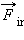 составляющие силы
составляющие силы  действующей на элемент Δ m i твердого тела.
действующей на элемент Δ m i твердого тела.
 массы Δ m i. Второй закон Ньютона, записанный в скалярной форме, дает
массы Δ m i. Второй закон Ньютона, записанный в скалярной форме, дает – угловое ускорение всех точек твердого тела.
– угловое ускорение всех точек твердого тела.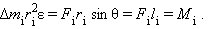
 , M i – момент силы.
, M i – момент силы.
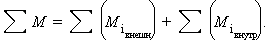
 ,
,  ,
,  определяются как векторы, направленные по оси вращения.
определяются как векторы, направленные по оси вращения. (см. §1.16). Аналогично, при изучении вращательного движения вводится понятие момента импульса.
(см. §1.16). Аналогично, при изучении вращательного движения вводится понятие момента импульса. уравнение вращательного движения можно представить в виде:
уравнение вращательного движения можно представить в виде: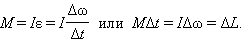
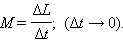

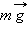 и силы реакции
и силы реакции  относительно оси O равны нулю. Момент M создает только сила трения: M = F тр R.
относительно оси O равны нулю. Момент M создает только сила трения: M = F тр R.

 а у сплошного однородного цилиндра
а у сплошного однородного цилиндра 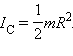 Следовательно, шар будет скатываться быстрее цилиндра.
Следовательно, шар будет скатываться быстрее цилиндра.


