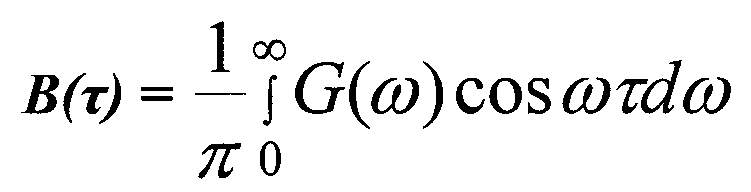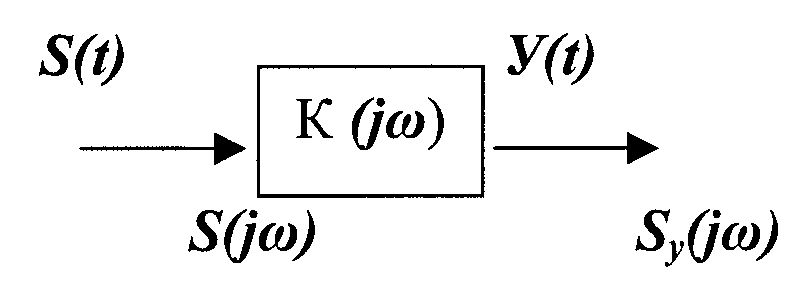ПВМ – преобразователь
АД – амплитудный детектор ПД – пиковый детектор
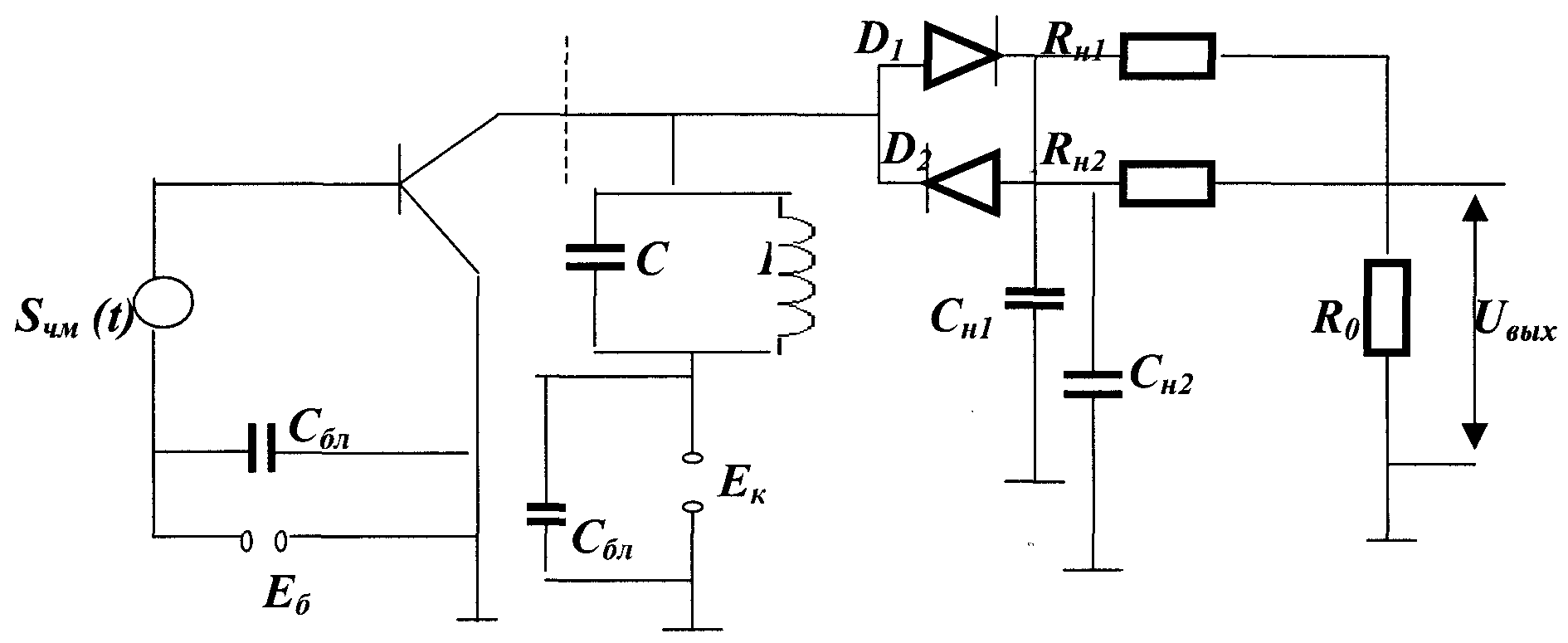
ЧАСТОТНЫЙ ДЕТЕКТОР С ОДИНОЧНЫМ РАССТРОЕННЫМ КОНТУРОМ Работает по принципу преобразователя ЧМ сигнала в AM, с дальнейшим детектированием при помощи АД.
Если будет изменяться расстройка колебательного контура, это приведет к изменению колебательного контура эквивалентного входного сопротивления колебательного контура, следовательно будет изменен Uк(ω)=I∙ Zк(ω)
ЧАСТОТНЫЙ ДЕТЕКТОР С ДВУМЯ ВЗАИМНО РАССТРОЕННЫМИ КОНТУРАМИ
Недостатки: 1. Наличие катушек индуктивности. 2. Все три катушки настраиваются на разные частоты. ЧАСТОТНЫЙ ДЕТЕКТОР С ДВУМЯ ВЗАИМНО НАСТРОЕННЫМИ КОНТУРАМИ
Работает по принципу преобразователя ЧМ сигнала в ФМ сигнал.
Лекция-30 КВАДРАТУРНЫЙ ЧД
ЧД КАК СЧЕТЧИК ИМПУЛЬСОВ. Работает по принципу преобразователя ЧМ сигнала в последовательность импульсов с постоянной амплитудой и шириной, и с частотой повторений равной частоте входного модулированного сигнала.
ГАРМОНИЧЕСКИЙ ЧД (ГЧД). ЧМ преобразуется в ФМ сигнал, дальнейшее детектирование при помощи пикового детектора, при этом полезно используется токи первой и второй гармоника входного сигнала.
Лекция-31 СИГНАЛ И ПОМЕХА КАК СЛУЧАЙНЫЙ ПРОЦЕСС 1. Сигнал делится на: непрерывный, и дискретный. 2. Сигналы: сложные и простые. 3. Сигналы: детерминированные и случайные.
Наибольшими общими характеристиками случайных процессов являются интегральный, дифференциальный законы распределения. Законы распределения делятся на одномерные и двумерные. Одномерный интегральный закон распределения
Наиболее полными характеристиками случайных процессов являются его п - мерный интегральный и дифференциальный закон распределений. Наиболее часто для оценки случайных процессов пользуются: 1. Математическим ожиданием, усредненным по времени и по множествам (ансамблем) М(х). 2. Функция корреляции делится на: 1. Функцию автокорреляции. 2. Функцию взаимной корреляции. Функция автокорреляции.
Функция взаимной корреляции.
Все случайные процессы делятся на стационарные и нестационарные. Под стационарным процессом в широком смысле понимают такой процесс, n мерный закон распределения которого на зависит от начала отсчета времени. Стационарный случайный процесс в узком смысле - это такой процесс, математическое ожидание и дисперсия которого не зависит от начала отсчета времени. А функция корреляции Вхх (τ) также не зависит от отдельных значений t1 и t2, а зависит от разности t2 – t1= τ;. Не стационарный процесс - такой процесс, в котором функция корреляции, дисперсия, математическое ожидание зависят от начала отсчета времени. Коэффициент автокорреляции:
Коэффициент взаимной корреляции:
Стационарные случайные процессы обладают свойством эргодичности.
Лекция-32 СВОЙСТВА ФУНКЦИИ КОРРЕЛЯЦИИ 1. Функция корреляции - четная функция. В(τ) =В(-τ) 2. Вхх (τ) =σ 2, где σ 2 - дисперсия случайного процесса. 3. Вхх(τ)≥ Вхх(τ) 4. Если Rxx (τ) = 1 при τ = 0, тогда Rxx (τ) = 0 при τ ≠ 0, то такой процесс называется чисто случайным процессом. 5. Если стационарный случайный процесс не содержит регулярной составляющей, то его функция корреляции Вхх (τ) → а2. 6. Если стационарный случайный процесс содержит регулярную составляющую Вхх (τ) → а2, где а2 - квадрат амплитуды регулярно составляющей. 7. Функция автокорреляции периодического процесса также является периодической с тем же периодом, что и сам процесс. Вху периодический процесс не зависит от его начальной фазы. ИНТЕРВАЛ КОРРЕЛЯЦИИ Для стационарных случайных процессов можно указать такой промежуток времени Δ τ, что как только Δ τ > τ, то его отдельные значения становятся независимыми. Этот промежуток времени Δ τ, в пределах которого существует взаимосвязь между отельными значениями случайного процесса, называется интервалом корреляции. Δ τ - определяется шириной основания прямоугольника с единичной высотой, площадь которого равно площади, ограниченной кривой Вхх.
РАЗЛОЖЕНИЕ СИГНАЛОВ НА ЭЛЕМЕНТАРНЫЕ СОСТАВЛЯЮЩИЕ. Реальные сигналы носят случайные характер и имеют сложную форму
1. Элементарные сигналы должны быть взаимно независимыми, и будучи умноженными на ак, мы должны получить S(t). 2. Значения весовых коэффициентов ак не должны зависеть от количества элементных составляющих.
Этим двум требованиям отвечает ортогональная функция.
Лекция-33 РАЗЛОЖЕНИЕ СИГНАЛА В ТРИГОНОМЕТРИЧЕСКИЙ РЯД ФУРЬЕ.
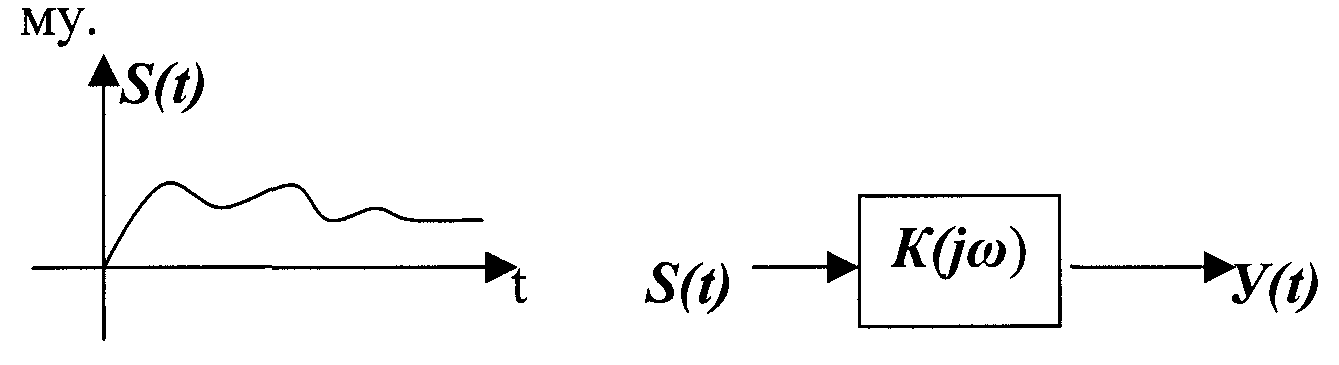
ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИГНАЛА. Пусть S(t) носит случайный характер.
Спектральная плотность мощности: 1. Формулы Винер-Хинчена
Эти формулы связывают функцию корреляции с энергетическим спектром.
Если В(τ) четная функция, тогда
ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ СИГНАЛОВ (ПРОЦЕССОВ) ЧЕРЕЗ РАДИОТЕХНИЧЕСКОЕ ЗВЕНО
Лекция-34 ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА ЧЕРЕЗ ЛЭЦ При прохождении случайных процессов (сигналов), через линейные радиотехнические устройства в общем случае изменяются все числовые характеристики отклика (математическое ожидание, дисперсия...) Только в одном случае, когда входной процесс (сигнал) подчиняется нормальному закону распределения, то и отклик Y(t) подчиняется нормальному закону распределения. Если входной сигнал имеет спектр Δ ω сп > > ω эфф или Δ ω пплс , то происходит нормализация закона распределения отклика, т.е. отклик будет подчиняться нормальному закону распределения. Согласно центральной предельной теореме. По теореме вероятности: сумма больше числа случайных величин подчиняется нормальному закону распределения. Флуктуационными помеху называют узкополосной, если интервал корреляции Δ τ > tуст переходных процессов линейной системы. Если помеха широкополосная, то функция корреляции
Флуктуационную помеху называют гладкой или помехой белого шума. Сигнал по КС передается по AM g = С/П
|






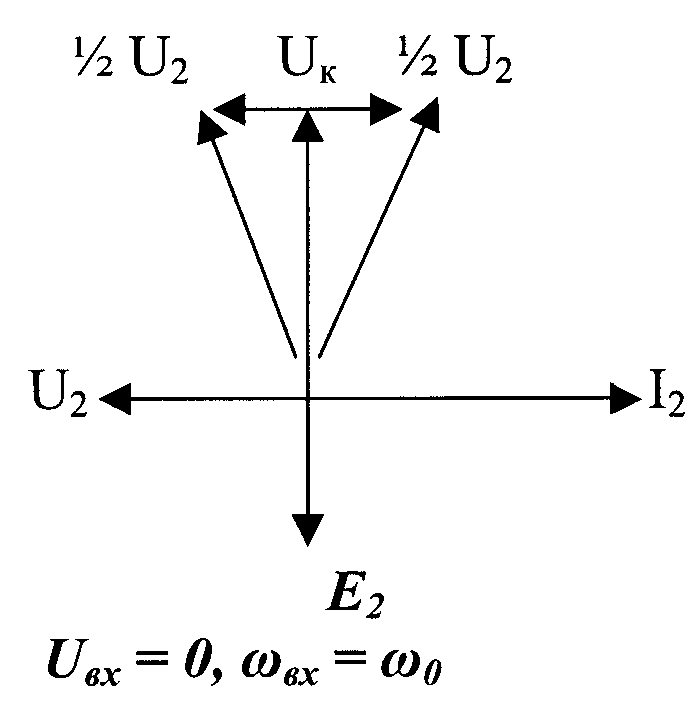







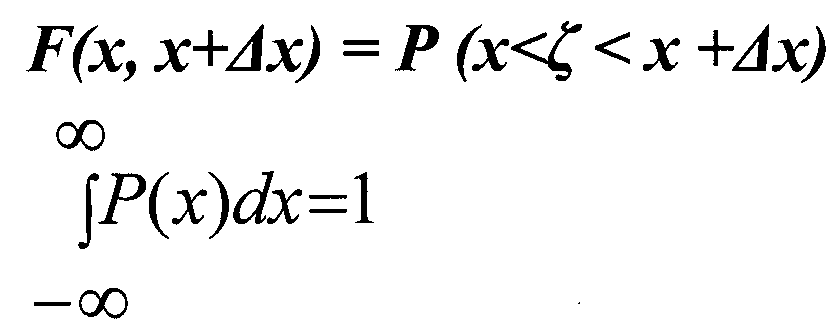
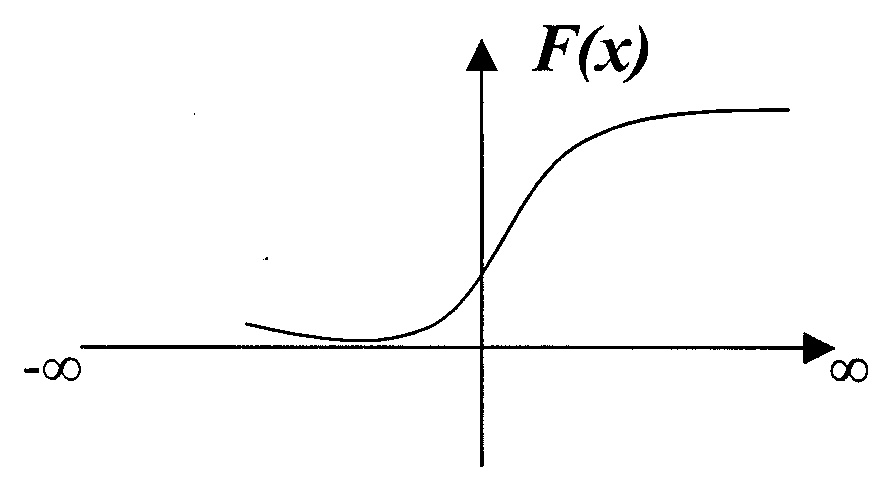

 плотность вероятности
плотность вероятности


















 (1)
(1) (2)
(2) 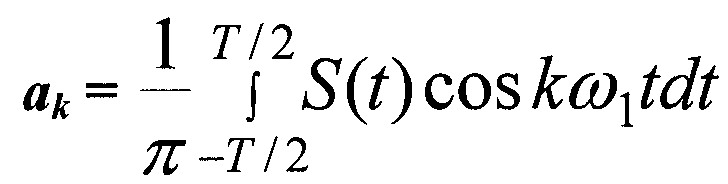 (3)
(3)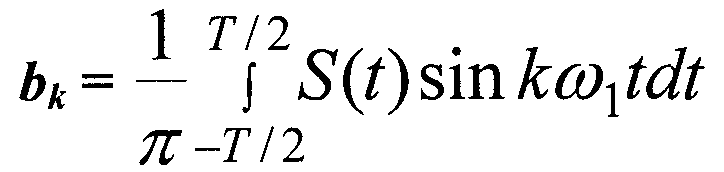 (4)
(4)  (5)
(5) - текущий спектр для сигнала длительности Т.
- текущий спектр для сигнала длительности Т.