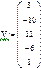Нахождение корней полинома. Если функция f (х) является полиномом, то все его корни можно определить, используя встроенную функцию polyroots(v),

Если функция f (х) является полиномом, то все его корни можно определить, используя встроенную функцию polyroots (v),

где v — вектор, составленный из коэффициентов полинома.

Поскольку полином N -й степени имеет ровно N корней (некоторые из них могут быть кратными), вектор v должен состоять из N+1 элемента. Результатом действия функции poiyroots является вектор, составленный из N корней рассматриваемого полинома. При этом нет надобности вводить какое-либо начальное приближение, как для функции root. Ниже приведен алгоритм решения полинома на примере поиска корней полинома четвертой степени .

Шаг 1. Записать полином (без правой части), выделить указателем переменную, коэффициенты при которой необходимо определить (Рис. 6.2). Переменная х при этом будет выделена темным фоном.

Шаг 2. Выбрать: Главное меню, Символы, Коэффициенты полинома. Появляется вектор столбец с коэффициентами, в котором первым элементом является свободный член полинома, вторым — коэффициент при х ₁ и т. д. Соответственно, последним n +1 элементом вектора должен быть коэффициент при старшей степени.

Шаг 3. Задайте вектор (например, V), поставьте знак присваивания, скопируйте полученный ранее вектор степеней полинома в буфер обмена (копировать) и вставьте его в правую часть созданного вектора V (вставить).

Шаг 4. Запишите (можно воспользоваться режимом «вставка функции» (Рис. 6.3)) функцию polyroots, единственным аргументом которой будет сформированный на шаге 3 вектор V. Поставьте знак равенства и получите вектор корней полинома, среди которых могут быть и комплексные числа.