Одно уравнение с одним неизвестным

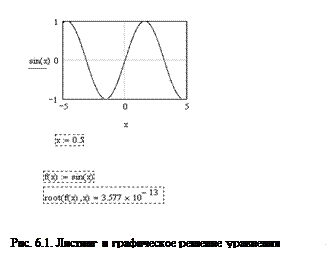
Наиболее распространенной задачей в математике является решение уравнений. Для решения уравнения необходимо задать его в виде формулы. Рассмотрим решение алгебраического уравнения с одним неизвестным f (x) = 0. Например, рассмотрим решение уравнения sin (x) = 0.

Для решения таких уравнений Mathcad имеет встроенную функцию root, которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента и, соответственно, работает несколько по-разному.

root(f(х), х); либо root(f(х), х, а, b);

f (х) — скалярная функция, определяющая уравнение (sin(x) в нашем примере);

х — скалярная переменная, относительно которой решается уравнение;

а, b — границы интервала, внутри которого происходит поиск корня.

Явный вид функции f (х) может быть определен непосредственно в теле функции roo t.

Первый тип функции root требует дополнительного задания начального значения переменной х. Для этого нужно просто предварительно присвоить х некоторое число, вблизи которого будет производиться поиск корня уравнения. Таким образом, присвоение начального значения требует априорной информации о примерной локализации корня. Данная проблема может быть легко решена, если предварительно построить график функции, заданной уравнением, по графику найти приблизительное значение величины х, при которой y обращается в нуль (кривая графика пересекает ось ОХ Рис. 6.1).

Хотя данное уравнение имеет бесконечное количество корней, Mathcad находит (с заданной точностью) только один из них, лежащий наиболее близко к х = 0.5 (т.е. ). Если задать другое начальное значение, например х = 3, то решением будет другой корень уравнения и т. д. Таким образом, для поиска корня средствами Mathcad требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который называется методом секущих.

 

 

В вычислениях, приведенных в листинге рис. 6.1, погрешность вычисления TOL=0.001 (установлена по умолчанию). Чем меньше константа TOL, тем ближе к нулю будет значение f (x) в найденном корне, но тем больше времени будет затрачено вычислительным процессором Mathcad на его поиск.

Если уравнение не имеет корней, то при попытке найти решение будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в области локального максимума или минимума f (х).

 

Иногда удобнее задавать не начальное приближение к корню, а интервал [а, b], внутри которого корень заведомо находится. В этом случае следует использовать функцию root с четырьмя аргументами, и присваивать начальное значение х не нужно. Поиск корня будет осуществлен в промежутке между а и b.

 

 

Когда root имеет четыре аргумента, следует помнить о двух ее особенностях:

- внутри интервала [ а, b ] не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно;

- значения f (а) и f (b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.

Если уравнение не имеет действительных корней, но имеет мнимые, то их также можно найти. В листинге 6.2. приведен пример, в котором уравнение x2+1=0, имеющее два чисто мнимых корня, решается два раза с разными начальными значениями. При задании начального значения - 0.5 численный метод отыскивает первый корень (отрицательную мнимую единицу -i), а при начальном значении 0.5 находится и второй корень (i).

 

 

 

Для решения таких уравнений второй вид функции root ( с четырьмя, а не с двумя аргументами) неприменим, поскольку функция f (х) является положительно определенной, и указать интервал, на границах которого она имела бы разный знак, невозможно.

Функция f (х) может быть функцией не только х, а любого количества аргументов. Именно поэтому в самой функции root необходимо определить, относительно какого из аргументов следует решить уравнение.