Гальванического элемента
При контакте двух любых фаз на границе их раздела возникает двойной электрический слой (ДЭС), состоящий из равных по величине, но противоположных по знаку электрических зарядов. Это обусловлено тем, что заряженные частицы (ионы, электроны) в разных фазах находятся в разных условиях и, следовательно, имеют разные химические потенциалы. Согласно второму закону термодинамики, самопроизвольно частицы переходят из фазы с большим химическим потенциалом в фазу, где их химический потенциал меньше, до тех пор, пока свободная энергия системы (G) не станет минимальной. Поэтому каждая фаза приобретает заряд, и на границе раздела фаз возникает разность электрических потенциалов (скачок потенциала). Скачки потенциала возникают на границе металл I/ метал II (контактный потенциал), на границах металл/ раствор и на границе двух растворов (диффузионный потенциал). Механизм образования ДЭС различен и зависит от природы граничащих фаз. Диффузионная разность потенциалов (или просто диффузионный потенциал – Ед) возникает на границе соприкасающихся растворов электролитов благодаря тому, что диффузия катионов и анионов из одного раствора в другой происходит с различной скоростью, что и ведёт к образованию ДЭС в тонком слое в области контакта растворов. Для уменьшения диффузионного потенциала растворы электролитов в электрохимических системах соединяют с помощью солевого мостика, наполненного насыщенным раствором такого электролита, у которого подвижности и скорости диффузии катиона и аниона близки. Обычно в этих целях используют водные растворы KCl, NH4Cl, KNO3, NH4NO3 и др. При погружении металла в водный раствор его соли часть катионов кристаллической решётки сольватируется полярными молекулами воды и переходит в раствор, придавая ему положительный заряд. Металл, в котором появился избыток электронов, заряжается отрицательно. Отрицательный заряд металла препятствует дальнейшему переходу катионов в раствор, и в системе устанавливается равновесие, которому соответствует определённое значение равновесного скачка потенциала между металлом и раствором, величина которого зависит от природы металла, от концентрации ионов металла в растворе и температуры. Некоторые металлы (например, золото, платина) обладают столь прочной кристаллической решёткой, что катионы не могут освободиться. При погружении такого металла в электролит, содержащий ионы с элементами, находящимися в различных степенях окисления (такие системы называются окислительно-восстановительными, или редокс-электродами), будет происходить обмен электронами между инертным электродом и ионами, что также ведёт к образованию двойного электрического слоя и возникновению равновесного скачка потенциала. Устройство, которое позволяет получить электрическую работу за счёт энергии химической реакции, называется гальваническим элементом. Гальванический элемент состоит из двух электродов, представляющих собой систему из электронного проводника (металла) и раствора одного или нескольких электролитов, находящихся с ним в контакте. На границе фаз такой системы, как было рассмотрено выше, существует скачок потенциала.
Рис. 1. Схема гальванического элемента
Гальванический элемент, изображённый на рисунке, состоит из электрода I рода (слева) и редокс-электрода (справа). Разность потенциалов на концах разомкнутого гальванического элемента называется его электродвижущей силой (эдс). Электродвижущая сила гальванического элемента (Е) определяется из скачков потенциала на границах фаз. В разомкнутом обратимом гальваническом элементе на фазовых границах образуется двойной электрический слой и устанавливается равновесие, которому соответствует равновесный скачок потенциала. Если же замкнуть электроды проводником первого рода (соединить металлическим проводом), то равновесие нарушается. Поскольку электрические потенциалы на концах электродов неодинаковы, то электроны с более отрицательного электрода (Е Итак, при работе данного гальванического элемента протекают следующие процессы: 1) реакция окисления цинка Zn - 2e → Zn2+ Процессы окисления в электрохимии получили название анодных процессов, а электрод, на котором идёт процесс окисления, называют анодом; 2) реакция восстановления ионов железа Fe3+ + e → Fe2+ Процессы восстановления в электрохимии получили название катодных процессов, а электрод, на котором идёт процесс восстановления, называют катодом; 3) движение электронов во внешней цепи; 4) движение ионов в растворе: анионов (SO А (-): Zn - 2e → Zn2+ │ 1 К (+): Fe3+ + e → Fe2+ │ 2
Zn + 2 Fe3+ → Zn2+ + 2 Fe2+ или Zn + Fe2(SO4)3 → ZnSO4 + 2 FeSO4 В результате этой химической реакции в гальваническом элементе возникает движение электронов во внешней цепи и ионов внутри элемента, т.е. электрический ток, поэтому суммарная химическая реакция, протекающая в гальваническом элементе, называется токообразующей (или потенциалообразующей). При схематической записи, заменяющей рисунок гальванического элемента, слева указывается материал более отрицательного электрода, затем примыкающий к нему раствор, причём твёрдая фаза отделяется от раствора одной вертикальной чертой. Далее указывается двумя вертикальными чертами солевой мостик, раствор более положительного электрода и, наконец, металл, из которого сделан этот электрод (раствор от металла отделяется одной вертикальной чертой). Рассмотренный нами гальванический элемент можно представить в следующем виде:
Если в гальваническом элементе протекает токообразующая реакция ν 1А + ν 2В → ν 3С + ν 4D, то электродвижущую силу гальванического элемента при 25º С можно рассчитать по уравнению Нернста: Е = Е0 - где Измерить абсолютное значение отдельного электродного потенциала невозможно. Можно определить только относительные величины, характеризующие электродные потенциалы. Эдс элемента равна разности равновесных потенциалов положительного электрода (в элементе катода) и отрицательного электрода (в элементе анода). Если потенциал одного из электродов принять равным рулю, то относительный потенциал второго электрода будет равен эдс. Таким образом, можно определить потенциал любого электрода. Для электродов, в состав которых входят водные растворы электролитов, в качестве стандартного выбирают нормальный водородный электрод, электродный потенциал которого условно принят за нуль при любой температуре. Эта условная шкала потенциалов называется водородной шкалой. Водородный электрод – газовый электрод, обратимый относительно катиона Н+. Нормальным называют водородный электрод, который работает при давлении водорода в газовой фазе, равном 1 атмосфере, и активности ионов Н+ в растворе, равной 1.Равновесие на водородном электроде можно представить в виде: 2 Н+ + 2e ↔ Н2. Для определения потенциалов электродов по водородной шкале собирают гальванический элемент, одним из электродов которого является измеряемый, а вторым - стандартный водородный электрод. Электродным потенциалом по водородной шкале называют эдс элемента, составленного из этого электрода (справа) и нормального водородного электрода (слева), при условии, что диффузионный потенциал устранён. Электродный потенциал может быть величиной положительной или отрицательной в зависимости от окислительно-восстановительной способности металла и его ионов. Если в паре со стандартным водородным электродом стоит электрод более положительный, то его потенциал считают положительным, если более отрицательный, то отрицательным. Например, для редокс-электрода Fe3+, Fe2+│ Pt электродный потенциал есть эдс элемента:
в котором протекает токообразующая реакция: 2 Н+ - 2e → Н2 │ 1 Fe3+ + e → Fe2+ │ 2
H2 + 2 Fe3+ → 2 H+ + 2 Fe2+ Электродвижущая сила данного элемента по уравнению Нернста (113): Е = Е0 где Е0 = Так как в стандартном водородном электроде
где В общем случае, если потенциалопределяющий процесс на исследуемом электроде можно представить в виде: ν 1А1 + ν 2А2 → ν 3А3 + ν 4А4, то, чтобы получить выражение для электродного потенциала по водородной шкале, необходимо записать для электродной реакции уравнение Нернста: Еисслед.эл-да = и принять активности воды и индивидуальных веществ, находящихся в твёрдом фазовом состоянии, равными 1( Стандартные водородные потенциалы по водородной шкале определены для большинства электродов и приведены в справочной литературе, где они сведены в таблицу и расположены по возрастающему положительному значению. В этот электрохимический ряд включён и ряд напряжений металлических электродов. По значениям электродных потенциалов положительного (Е+) и отрицательного (Е-) электродов можно рассчитать электродвижущую силу (Е) элемента, составленного из этих электродов, если устранён диффузионный потенциал: Е = Е+ – Е- = Ек – Еа. (115) В зависимости от свойств веществ, участвующих в потенциалопределяющих процессах, принята следующая классификация электродов: электроды первого и второго рода, газовые, окислительно-восстановительные (редокс-электроды) и ионообменные. Рассмотрим некоторые из них подробнее. Электроды первого рода. К этим электродам относятся металлические электроды, обратимые относительно катионов. Уравнение токообразующей реакции на электродах, обратимых относительно катионов Ме│ Меn+ можно выразить следующим образом: Меn+ + nе → Ме. Электродный потенциал по водородной шкале согласно уравнению (114) и с учётом того, что активность твёрдого вещества при данной температуре постоянна и равна 1, имеет вид:
Чем более отрицательное значение имеет потенциал металла, тем более сильной восстановительной способностью он обладает. И наоборот, чем более положителен потенциал металлического электрода, тем более сильной окислительной способностью обладают его ионы. Окислительно-восстановительные электроды. Окислительно-восстановитель- ные (редокс -) электроды представляют собой инертный металл (платина, золото, иридий), погружённый в раствор, содержащий ионы, участвующие в окислительно-восстановительной реакции. Причём сам металл не участвует непосредственно в электродной реакции, а только обменивается электронами с участниками окислительно-восстановительных процессов. Для редокс-электродов характерно, что окисленная и восстановленная форма вещества находятся в одном растворе, а не выделяются на границах раздела фаз. В общем виде электродная реакция на таком электроде выглядит так: Ox + ne → Red. Схема электрода соответственно может быть записана в форме: Pt│ Ox, Red, где Ox – окисленная форма вещества, Red – восстановленная форма вещества. Уравнение Нернста для расчёта потенциала редокс-электрода имеет вид: ЕOx, Red = В более сложных случаях, когда в процессе принимают участие ионы ОН- или Н+, редокс-потенциалы зависят от рН. Например, для системы
в которой ионы
Под знаком логарифма в вышестоящем уравнении отсутствует активность воды, которая при электродных реакциях остаётся практически постоянной и учитывается в значении Е0. Подставляя численные значения величин R и F в уравнение и учитывая, что
Как следует из уравнения, редокс-потенциал мало зависит от активностей ионов Потенциал окислительно-восстановительных электродов служит мерой окислительной и восстановительной способности систем. Окислительная способность систем возрастает со сдвигом редокс-потенциала в сторону положительных значений. Восстановительная способность систем растёт со сдвигом потенциала в сторону отрицательных значений. Для определения направления окислительно-восстановительных процессов необходимо рассчитать эдс как разность потенциалов редокс-электродов, участвующих в данном процессе. Реакция будет протекать в том направлении, в котором эдс положительна. Например, реакция Sn2+ + 2Fe3+ ↔ Sn4+ + 2Fe3+ при
Концентрационные гальванические элементы (цепи). Концентрационные элементы составлены из двух качественно одинаковых полуэлементов – электродов любого рода, различающихся активностью ионов или веществ, участвующих в потенциалообразующем процессе. Например, для элемента Ag│ Ag+│ │ Ag+│ Ag │ C1 │ │ C2 │ на отрицательном электроде протекает процесс окисления, а на положительном – восстановления: (-): Ag – e → Ag+ (лев) (+): Ag+(пр) + e → Ag
Ag+(пр) → Ag+(лев). При суммировании уравнений электродных реакций получаем уравнение процесса, протекающего в гальваническом элементе, из которого очевидно, что в концентрационном элементе химическая реакция не протекает. Электрическая работа совершается за счёт процесса выравнивания концентраций потенциалообразующих ионов. Стандартная эдс концентрационного элемента равна 0 (Е0 = Е = или, заменив активность иона на среднеионную активность электролита, Е = где
Пример 21. Вычислить потенциал медного электрода в растворе, содержащем 1, 6 г CuSO4 в 200 см3 раствора при 25º С. Кажущаяся степень диссоциации соли в растворе равна 40%. Решение. Рассчитываем молярную концентрацию раствора:
Концентрация ионов меди в растворе равна
Электродный потенциал медного электрода вычисляем по уравнению (116):
Значение стандартного электродного потенциала медного электрода находим из справочных данных таблицы 6 Приложения и получаем:
Пример 22. Вычислить эдс гальванического элемента при 25º С Tl│ TlNO3│ │ CuSO4│ Cu │ 0, 2 н │ │ 0, 1M │ Кажущуюся степень диссоциации CuSO4 принять равной 40%, а TlNO3 – 80%. Решение. Из таблицы 6 Приложения находим стандартные потенциалы меди и таллия:
Используя формулу (115), получаем: Е =
Пример 22. Рассчитайте равновесный потенциал электрода, на котором протекает реакция по уравнению: PbO2 + 4H+ + 2e ↔ Pb2+ + 2H2O Активность иона Pb2+ равна 0, 1, рН 10, Т = 298 К. Решение. Потенциал окислительно-восстановительного электрода определяем по уравнению:
Активности веществ в твёрдом виде и активности воды принимаются постоянными и учитываются в значении Е0, поэтому уравнение для определения потенциала упрощается:
Подставляя численные значения R, T, F и преобразуя уравнение, получаем:
Поскольку lg
Подставив данные из условия задачи и табличные значения, получим:
Пример 23. Вычислить при 18º С эдс концентрационного элемента, состоящего из серебряных электродов, погружённых в 0, 1 н и 0, 01 н растворы нитрата серебра. При этой температуре эквивалентная электропроводность 0, 1 н раствора равна 94, 3 См·см2/моль, а 0, 01 н раствора AgNO3 – 107, 8 См·см2/моль. Решение. Эдс концентрационного элемента определяем по формуле (118). Для AgNO3 n=1. По электропроводности определяем α 0, 1 и α 0, 01 растворов AgNO3:
α 0, 1=
Вариант 1. 13. Вычислить при 25º С потенциал цинкового электрода, погруженного в 150 см3 раствора, содержащего 0, 2 г сульфата цинка. Степень диссоциации принять равной единице.
14. Какая токообразующая реакция протекает в гальваническом элементе: Zn│ ZnSO4 │ │ H2SO4│ H2(Pt) 0, 01 Какова эдс этого элемента?
15. Рассчитайте эдс гальванического элемента Ni │ NiSO4 │ │ NiSO4 │ Ni 1∙ 10-3 Вариант 2. 13. Вычислить при 25º С потенциал алюминиевого электрода, погруженного в 120 см3 раствора, содержащего 0, 1 г хлорида алюминия. Степень диссоциации принять равной единице.
14. Составьте схему гальванического элемента, в котором протекает следующая токообразующая реакция: 2 FeCl3 + SnCl2 = SnCl4 + 2 FeCl2.
15. Вычислить эдс гальванического элемента при 25º С Ni│ NiSO4 │ │ AgNO3 │ Ag │ 0, 005M│ │ 0, 005M│ Степень диссоциации солей принять за единицу. Вариант 3. 13. Вычислить при 25º С потенциал свинцового электрода, погруженного в 200 см3 раствора, содержащего 0, 1 г нитрата свинца. Степень диссоциации принять равной единице. 14. Составьте схему гальванического элемента, в котором протекает следующая токообразующая реакция: CuSO4 + H2 = Cu + H2SO4.
15. Вычислить при 25º С эдс элемента, образованного никелевым электродом, погружённым в 0, 05 М раствор NiSO4 и медным электродом, погружённым в 0, 02 М раствор CuSO4, считая диссоциацию солей полной.
Вариант 4. 13. Вычислить при 25º С потенциал никелевого электрода, погруженного в 200 см3 раствора, содержащего 0, 12 г нитрата никеля. Степень диссоциации принять равной единице.
14. Вычислить эдс гальванического элемента при 18º С Ag│ AgNO3│ │ AgNO3 │ Ag │ 0, 5 M │ │ 0, 05 M │ Удельная электропроводность 0, 05 М раствора 99, 5 См·см2/моль, а 0, 5 М раствора –77, 5 См·см2/моль.
15. Вычислить эдс гальванического элемента при 25º С Zn │ ZnSO4│ │ CdSO4 │ Cd │ 0, 2 M │ │ 0, 1 M │ Кажущаяся степень диссоциации CdSO4 60 %, а CdSO4 – 40 %.
Вариант 5. 13. Вычислить при 25º С потенциал магниевого электрода, погруженного в 150 см3 раствора, содержащего 0, 16 г сульфата магния. Кажущаяся степень диссоциации равна 65%. 14. Докажите, может ли данная реакция протекать самопроизвольно в прямом направлении: 2KI + Br2 = 2 KBr + I2?
15. Вычислить эдс гальванического элемента при 25º С Tl │ Tl2SO4 │ │ CuSO4 │ Cu Tl │ 0, 02 M │ │ 0, 1 M │ Кажущаяся степень диссоциации CuSO4 равна 40 %, а для Tl2SO4 – 87 %.
Вариант 6. 13. Чему равен потенциал платинового электрода, погруженного в раствор, содержащий 1·10-3 моль/дм3 Fe2(SO4)3 и 0, 02 моль/дм3 FeSO4 по отношению к стандартному водородному электроду? 14. Докажите, может ли данная реакция протекать самопроизвольно в прямом направлении: Sn+4 + 2 Fe+2 = Sn+2 + 2 Fe+3?
15. Вычислить эдс гальванического элемента при 25º С Pb │ Pb(NO3)2 │ │ AgNO3 │ Ag │ 0, 05 M │ │ 0, 1 M │ Кажущаяся степень диссоциации Pb(NO3)2 равна 75 %, а для AgNO3 – 81 %.
Вариант 7. 13. При какой концентрации ионов меди в растворе сульфата меди электродный потенциал меди будет равен нулю? температура 25º С. 14. Докажите, может ли данная реакция протекать самопроизвольно в прямом направлении: MnO
15. Вычислить эдс гальванического элемента Cd │ Cd(NO3)2 │ │ AgNO3 │ Ag │ 0, 5 M │ │ 0, 1 M │ Кажущаяся степень диссоциации Cd(NO3)2 в растворе равна 48 %, а AgNO3 – 81 %. Температура раствора 25º С. Вариант 8. 13. Вычислить при 25º С потенциал цинкового электрода в 0, 05 н растворе хлорида цинка. Кажущуюся степень диссоциации принять равной 80%.
14. Составьте уравнения полуреакций в окислительно-восстановительной системе: KIO3 + FeSO4 + H2SO4 = I2 + Fe2(SO4)3 + K2SO4 + H2O Укажите, в каком направлении будет протекать процесс и вычислите эдс окислительно-восстановительного гальванического элемента, работающего на основе данной реакции.
15. Какие процессы будут протекать на катоде и аноде гальванического элемента Al │ соль Al │ │ AgNO3 │ Ag │ 0, 01 M │ │ 0, 2 M │ Вычислить эдс этого элемента при 25º С, если считать, что соли полностью диссоциированы.
Вариант 9. 13. Вычислить потенциал кадмия, погруженного в раствор с концентрацией ионов кадмия 0, 005 г-ион/дм3 при 25º С.
14. Из каких полуэлементов следует составить гальванический элемент, чтобы его эдс была максимальной: 1) Ca2+/Ca и Au3+/Au; 2) Zn2+/Zn и Fe2+/Fe; 3) Ni2+/Ni и Pb2+/Pb; 4) Mg2+/Mg и Cd2+/Cd; 5) Fe2+/Fe и Ni2+/Ni?
15. Определить концентрацию раствора Ni(NO3)2, если эдс элемента Со │ Co(NO3)2 │ │ Ni(NO3)2 │ Ni │ 0, 1 M │ │? M │ была равна нулю. Степень диссоциации для каждой из солей принять равной единице. Температура 25º С.
Вариант 10. 13. Вычислить потенциал серебра, погруженного в раствор с концентрацией ионов серебра 0, 02 г-ион/дм3 при 25º С.
14. Из каких полуэлементов следует составить гальванический элемент, чтобы его эдс была максимальной: 1) Cu2+/Cu и Pb2+ /Pb; 2) Cr3+/Cr и Fe2+/Fe; 3) Pb2+/Pb и Cr3+/Cr; 4) Cr3+/Cr и Cu2+/Cu; 5) Pb2+/Pb и Fe2+/Fe?
15. При 25º С эдс гальванического элемента Zn │ ZnSO4 │ │ ZnSO4 │ Zn │ 0, 5 M │ │ 0, 05 M │ равна 0, 018 В. Вычислить кажущуюся степень диссоциации сульфата цинка в более концентрированном растворе, если в более разбавленном растворе она равна 35 %.
|


 = - 0, 763 В) перемещаются на более положительный электрод (Е
= - 0, 763 В) перемещаются на более положительный электрод (Е 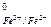 = + 0, 771 В). Это нарушает равновесие в двойном электрическом слое отрицательного электрода, на котором оказывается меньше электронов, чем необходимо для равновесия, и положительного электрода, где электронов оказывается больше. Для восстановления равновесия на границах фаз пойдут реакции, в результате которых на левом (отрицательном) электроде должны освобождаться электроны, а на правом (положительном) – поглощаться.
= + 0, 771 В). Это нарушает равновесие в двойном электрическом слое отрицательного электрода, на котором оказывается меньше электронов, чем необходимо для равновесия, и положительного электрода, где электронов оказывается больше. Для восстановления равновесия на границах фаз пойдут реакции, в результате которых на левом (отрицательном) электроде должны освобождаться электроны, а на правом (положительном) – поглощаться.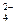 ) к аноду, катионов (Fe3+, Fe2+, Zn2+) к катоду. Движение ионов в растворе замыкает электрическую цепь гальванического элемента. Суммируя электродные реакции, получаем:
) к аноду, катионов (Fe3+, Fe2+, Zn2+) к катоду. Движение ионов в растворе замыкает электрическую цепь гальванического элемента. Суммируя электродные реакции, получаем:
 Zn│ Zn2+│ Fe3+, Fe2+│ Pt
Zn│ Zn2+│ Fe3+, Fe2+│ Pt , (113)
, (113) – активности участников реакции и Е0 =
– активности участников реакции и Е0 =  - стандартная электродвижущая сила элемента. При активностях реагентов и продуктов реакции, равных единице, т.е. при
- стандартная электродвижущая сила элемента. При активностях реагентов и продуктов реакции, равных единице, т.е. при  , получаем Е = Е0. Стандартной называется эдс элемента, если парциальные относительные давления исходных веществ и продуктов реакции равны единице или активности исходных веществ и продуктов реакции равны единице.
, получаем Е = Е0. Стандартной называется эдс элемента, если парциальные относительные давления исходных веществ и продуктов реакции равны единице или активности исходных веществ и продуктов реакции равны единице.
 (Pt) H2│ H+│ Fe3+, Fe2+│ Pt,
(Pt) H2│ H+│ Fe3+, Fe2+│ Pt,
 ,
, - стандартная эдс элемента, которую можно принять равной стандартному потенциалу исследуемого электрода, поскольку
- стандартная эдс элемента, которую можно принять равной стандартному потенциалу исследуемого электрода, поскольку  .
. и
и  , то после преобразования уравнения для электродного потенциала исследуемого редокс-элемента получаем:
, то после преобразования уравнения для электродного потенциала исследуемого редокс-элемента получаем: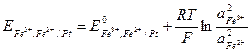 ,
,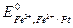 - стандартный электродный потенциал, т.е. потенциал электрода, в котором активности всех потенциалопределяющих ионов равны 1.
- стандартный электродный потенциал, т.е. потенциал электрода, в котором активности всех потенциалопределяющих ионов равны 1. (114)
(114) ).
). . (116)
. (116) . (117)
. (117)
 являются окисленной формой вещества, а ионы
являются окисленной формой вещества, а ионы  - восстановленной формой вещества, потенциал определяется уравнением:
- восстановленной формой вещества, потенциал определяется уравнением: .
.
 , получаем для 298К:
, получаем для 298К:
 пойдёт в прямом направлении, так как эдс положительна при условии, что электрод Fe3+/Fe2+ является катодом, т.е. электродом окислителем:
пойдёт в прямом направлении, так как эдс положительна при условии, что электрод Fe3+/Fe2+ является катодом, т.е. электродом окислителем: =
= 


 ), тогда в соответствии с уравнением Нернста для нашего серебряного концентрационного элемента имеем:
), тогда в соответствии с уравнением Нернста для нашего серебряного концентрационного элемента имеем:
 , (118)
, (118) - среднеионная активность растворов правого и левого электродов.
- среднеионная активность растворов правого и левого электродов. моль/л.
моль/л. г-ион/л.
г-ион/л. .
.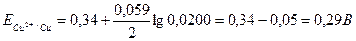 .
. .
. .
. .
. .
. .
. = - рН, то уравнение приобретает вид:
= - рН, то уравнение приобретает вид: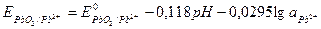 .
. .
. См·см2/моль,
См·см2/моль,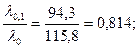 α 0, 01=
α 0, 01= 
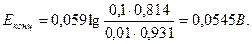
 рН=2
рН=2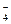 + 5 Fe2+ + 8H+ = Mn2+ + 5 Fe3+ + 4H2O?
+ 5 Fe2+ + 8H+ = Mn2+ + 5 Fe3+ + 4H2O?


