Классификация дисперсных систем по агрегатному состоянию
s = Для частиц шарообразной формы: s =
Удельная поверхность – это суммарная поверхность всех частиц вещества, общий объём которых составляет 1см3. Если принять форму частицы в виде куба с ребром1 см, то удельная поверхность s = Для частиц шарообразной формы: s = где r – радиус шарообразной частицы. По мере дробления вещества быстро растет число частиц, одновременно растет общая и удельная поверхность, а также запас свободной поверхностной энергии в системе. Вещество в конденсированном состоянии обладает поверхностной энергией, обусловленной нескомпенсированностью силовых полей частиц на поверхности раздела фаз. Свободная энергия единицы поверхности называется поверхностным натяжением или удельной поверхностной энергией σ. Поверхностное натяжение может быть измерено той работой, которую надо затратить на преодоление сил взаимодействия между молекулами для создания новой единицы поверхности. Согласно второму началу термодинамики в системах, обладающим избытком свободной энергии, могут самопроизвольно протекать процессы, приводящие к понижению запаса этой энергии. Таким самопроизвольным процессом, протекающим на границе раздела фаз, является адсорбция, которая в широком смысле означает всякое изменение концентрации вещества на поверхности раздела фаз. Если концентрация вещества в поверхностном слое возрастает, то адсорбция является положительной, а при уменьшении концентрации – отрицательной. Если вещество поглощается всем объемом другого вещества, то происходит абсорбция, если вещество концентрируется на поверхности раздела фаз, то имеет место адсорбция. Вещество, способное поглощать другое вещество, называется адсорбентом; вещество, которое может адсорбироваться – адсорбтивом; а уже адсорбированное вещество – адсорбатом. Процесс, обратный адсорбции, называется десорбцией. Зависимость адсорбции Г от равновесной концентрации С или от равновесного парциального давления р при постоянной температуре называется изотермой адсорбции. При выводе уравнения Лэнгмюра было сделано предположение, что поверхность адсорбента однородна и при максимальном заполнении образуется мономолекулярный слой. В этом случае уравнение адсорбции имеет вид; Г = Г∞ где Г∞ - адсорбция при максимальном заполнении; Ср – равновесная концентрация адсорбата; рр – равновесное давление адсорбата; Ка – константа равновесия процесса адсорбции. Отношение Г/ Г∞ называется степенью заполнения поверхности адсорбатом θ. Соответственно уравнения можно записать в виде: θ = При адсорбции в растворах может изменяться поверхностное натяжение. Адсорбирующиеся вещества могут понижать поверхностное натяжение (поверхностно-активные вещества – ПАВ), повышать поверхностное натяжение (поверхностно-инактивные вещества) и не влиять на поверхностное натяжение (поверхностно-неактивные вещества). Адсорбция на границе раствор – газ количественно характеризуется избытком вещества, содержащегося на 1 см2 поверхностного слоя (поверхностная концентрация раствора): Г = где S – площадь слоя, содержащего избыток растворенного вещества в количестве 1 моль. Поверхностный избыток Г можно определить по изменению поверхностного натяжения, обусловленного накоплением вещества в поверхностном слое, спользуя уравнение Гиббса: Г = - где с – концентрация вещества, кмоль/м2; R – универсальная газовая постоянная, Дж/кмоль∙ град; T – абсолютная температура; dσ /dc – изменение поверхностного натяжения с концентрацией при неизменной поверхности, Н/м. Для приближенных расчетов dσ /dc можно заменить на
тогда Г = - Из уравнения (126) вытекает, что если dσ /dc > 0, то Г< 0 (отрицательная адсорбция), а при dσ /dc < 0 Г> 0 (положительная адсорбция). При положительной адсорбции концентрация растворенного вещества больше в поверхностном слое по сравнению с глубиной фазы, а σ 2 < σ 1. Вещества, адсорбирующиеся положительно и вызывающие снижение поверхностного натяжения растворителя, называются поверхностно-активными (ПАВ). Молекулы ПАВ имеют гетерополярное строение, т.е. состоят из полярной функциональной группы (-COOH, Зависимость величины поверхностного натяжения раствора от концентрации ПАВ выражается эмпирическим уравнением Шишковского: σ = σ 0 – B ln(1 + Ac), (127) где σ 0 – поверхностное натяжение чистого растворителя; σ – поверхностное натяжение раствора; В – константа для всего гомологического ряда ПАВ; А – константа для конкретного ПАВ. Уравнение Шишковского в дифференциальной форме имеет вид:
Уравнение, связывающее величину гиббсовской адсорбции (Г) с константами уравнения Шишковского, имеет вид: Г = С другой стороны, величина адсорбции ПАВ в поверхностном слое связана с концентрацией уравнением Лэнгмюра: Г = Г∞ Отсюда константы Шишковского А и В обретают определенный физический смысл: В = Г∞ RT и A= Ka. Уравнение Шишковского справедливо при умеренных концентрациях, для больших концентраций поверхностное натяжение стремится к отрицательным значениям. Предельное значение поверхностного избытка при максимальном насыщении растворенным веществом поверхностного слоя обозначают Г∞ . Адсорбирующиеся вещества могут повышать величину поверхностного натяжения (поверхностно-инактивные вещества) и не влиять на поверхностное натяжение (поверхностно-неактивные вещества). При адсобции на границе раздела твердое тело – жидкость из-за невозможности экспериментального определения поверхностного натяжения количество адсорбированного вещества рассчитывают по изменению концентрации раствора. Зависимость количества вещества, адсорбированного 1 г адсорбента, от равновесной концентрации при постоянной температуре выражается эмпирической формулой Фрейндлиха
где х – количество адсорбированного вещества, г; m – количество адсорбента, г; с – концентрация раствора при достижении равновесия; a и n – постоянные величины, определяемые опытным путем. Постоянная 1/ n для многих адсорбентов и адсорбируемых веществ колеблется в пределах от 0, 1 до 0, 5. Константа а зависит от природы адсорбируемого вещества и изменяется в широких пределах. Постоянные а и 1/ n определяют графически. Логарифмируя (127), получаем уравнение прямой lg Определив значение х/m при двух концентрациях и построив график в логарифмических координатах, определяют константы a и n (рис.) lga=OA,
Пример 24. Определить суммарную поверхность частиц, если при дроблении 1 г серы получили частицы кубической формы с длиной ребра, равной 10-5 см. Плотность серы 2, 07 г/см3. Решение. Используем формулу (120) и получаем: s = 1 г серы занимает объём:
С учетом объёма 1 г серы получаем суммарную поверхность частиц: S = 6·105 см-1 · 0, 4831 см3 = 2, 9 · 105 см2 = 29 м2.
Пример 25. Определить число частиц, образующихся при дроблении 0, 2 см3 ртути на правильные кубики с длиной ребра 8 ·10-5см. Плотность ртути равна13, 546 г/см3. Решение. Находим массу 0, 2 см3 ртути: mHg = 0, 2 см3 · 13, 546 г/см3 = 2, 709 г. Определяем объём одной частицы: v = l 3 = (8 ·10-5)3 = 5, 12 ·10-16 cм3. Масса одной частицы будет равна: 5, 12 ·10-16 cм3 · 13, 546 г/см3 = 6, 94 ·10-15 г. Число частиц: N =
Пример 26. Определите поверхностный избыток (кмоль/м2) при 10°С для раствора, содержащего 50 мг/л пеларгоновой кислоты С8Н17СООН. Поверхностное натяжение воды при данной температуре 74, 22∙ 10-3 Н/м, а исследуемого раствора – 57, 0∙ 10-3Н/м. Решение. Для решения задачи воспользуемся формулой (126). Определяем концентрацию кислоты в кмоль/м2. По условиям задачи в 1 л содержится 0, 05 г кислоты. В 1м3 (или в 1000 л) этого раствора находится 0, 05 кг кислоты, т.е. 0, 05/158 кмоль/м3, где 158 – молекулярная масса пеларгоновой кислоты. Поскольку в воде концентрация пеларгоновой кислоты равна с1 = 0 и абсолютная температура раствора равна Т = 10+273 =283 К, то Г = = Г = Так как σ 2 < σ 1 и Г > 0, то адсорбция положительна.
Пример 27. При 293К зависимость поверхностного натяжения от концентрации водного раствора пропилового спирта выражается уравнением Шишковского: σ = σ 0 – 1, 44·10-3ln(1 + 6, 6c). Определите адсорбцию пропилового спирта на поверхности раздела водный раствор – воздух при концентрации 0, 25 моль/л. Решение. Из приведенного уравнения Шишковского следует, что А=6, 6 и В=1, 44·10-3. Подставим константы уравнения Шишковского в уравнение (129): Г = = 3, 57·10-7 моль/л
Пример 28. При адсорбционном насыщении при 293 К площадь, занимаемая молекулой изобутилового спирта, равна 2, 97·10-19 м2. Вычислите величину предельной адсорбции и постоянную В уравнения Шишковского. Решение. 1. Вычислим величину предельной адсорбции по уравнению (124): Г∞ = 2. Вычислим величину константы В уравнения Шишковского: В = Г∞ RT = 5, 6∙ 10-6моль/м2 ∙ 8, 314 Дж/(моль∙ К) ∙ 293 К = 0, 0136 Дж/м2.
Пример 29. На основе опытных данных, полученных при изучении адсорбции углем бензойной кислоты из раствора её в бензоле при 25°С, определить графически константы a и 1/ n в уравнении Фрейндлиха: с, моль/см3 0, 006 0, 025 0, 053 0, 118
Решение. Находим величины логарифмов для с и lg 0, 006 = -2, 2218; lg 0, 025 = -1, 6021; lg 0, 053 = - 1, 2757: lg 0, 118 = - 0, 9281; lg 0, 44 = -0, 3565; lg 0, 78 = - 0, 1079; lg 1, 04 = +0, 0170; lg 1, 44 = + 0, 1584
Строим график (рис.3), откладывая на оси ординат lg
а 1/ n является tgα. Из графика видно, что lg а ≈ 0, 53, следовательно, а ≈ 3, 4; tgα = =0, 4040; 1/ n = 0, 4 и n = 2, 5. В данном случае процесс адсорбции описывается уравнением:
Вариант 1 16 Найдите общую поверхность 1кг сферических частиц угля, если средний диаметр частиц 7∙ 10-2мм, а плотность угля – 1, 8∙ 103 кг/м3.
17 Определите поверхностный избыток (кмоль/м2) для 20-%-ного раствора серной кислоты при 18º С, если поверхностное натяжение раствора равно 75, 2∙ 10-3Н/м2, а воды – 73, 05∙ 10-3Н/м2. Плотность 20%-ного раствора серной кислоты 1, 143 г/см3.
18 По уравнению Фрейндлиха вычислить равновесную концентрацию уксусной кислоты, если 1г угля адсорбирует 3, 76 ммоль уксусной кислоты. Константы Кф=2, 82; n=2, 44.
Вариант 2 16 Удельная поверхность силикагеля равна 8, 3∙ 103 м2/кг. Рассчитайте средний диаметр частиц силикагеля, если его плотность равна 2, 2г/см3.
17 Определите поверхностный избыток (кмоль/м2) для водных растворов фенола при 20º С на основании приведённых величин поверхностного натяжения: Концентрация фенола, кмоль/м3 0, 0156 0, 0625 Поверхностное натяжение, Н/м2 58, 2∙ 10-3 43, 3∙ 10-3 Поверхностное натяжение воды при 20º С – 72, 75∙ 10-3Н/м2.
18 При изучении адсорбции ацетона древесным активированным углем при 20º С были получены следующие данные: Концентрация ацетона в растворе, моль/л 2, 34 14, 65 88, 62 177, 69 268, 97 Количество адсорбированного ацетона 1гугля, моль/г 0, 208 0, 618 1, 50 2, 08 2, 88 Графически определить постоянные Кф и n уравнения изотермы Фрейндлиха.
Вариант 3 16 Поверхностное натяжение на границе ртуть-воздух равно 72, 75∙ 10-3Дж/м2. Чему равна избыточная поверхностная энергия капли ртути диаметром 1, 2мм.
17 Определить поверхностный избыток (кмоль/л) и знак его для 20%-ного раствора едкого натра при 20º С, если поверхностное натяжение этого раствора равно 85, 8∙ 10-3Н/м2. Поверхностное натяжение воды при этой температуре равно 72, 75∙ 10-3Н/м2. Плотность 20%-ного раствора едкого натра 1, 219г/см3.
18 Определите графически константы Кф и n в уравнении изотермы адсорбции Фрейндлиха, если С, моль/см3 0, 268 0, 471 0, 882 А, моль/г 1.55 2, 04 2, 48
Вариант 4 16 Вычислить суммарную поверхность и число коллоидных частиц, которые получаются из 2г платины, раздробленной на правильные кубики с длиной ребра 10-6см. Плотность платины 21, 4г/см3.
17 Определить поверхностный избыток (кмоль/м2) для водных растворов изовалериановой кислоты при 15º С, пользуясь следующими данными: Концентрация кислоты, кмоль/м3 0, 0312 0, 25 Поверхностное натяжение, Н/м2 57, 5∙ 10-3 35, 0∙ 10-3 Поверхностное натяжение воды при 15º С 73, 49∙ 10-3Н/м2.
18 Определите графически константы Кф и n в уравнении изотермы адсорбции Фрейндлиха, если С, моль/см3 0, 018 0, 031 0, 062 0, 126 А, моль/г 0.467 0, 624 0, 801 1, 110
Вариант 5 16 Вычислить суммарную поверхность и число коллоидных частиц, которые могут получиться из 1гзолота, раздробленного на правильные кубики с длиной ребра 10-6см. Плотность золота 19, 3 г/см3.
17 Определите поверхностный избыток (кмоль/м2) и знак его при 15°С для водного раствора, содержащего 29 г/л ацетона, если поверхностное натяжение раствора 59, 410-3 Н\м. Поверхностное натяжение воды при этой температуре равно 73, 49∙ 10-3Н/м2.
18 Постройте график изотермы адсорбции в координатах с, моль/см3 0, 018 0, 031 0, 062 0, 126 0, 268 0, 471 0, 882
Вариант 6 16 Допуская, что в коллоидном растворе серебра каждая частица представляет собой куб с длиной ребра 4∙ 10-6см и плотностью 10, 5г/см3, рассчитать: а) сколько коллоидных частиц может получиться из 0, 1г серебра; б) чему равна общая поверхность всех серебряных частиц.
17 Вычислите адсорбцию масляной кислоты на поверхности водного раствора с воздухом при 293 К и концентрации 0, 5 моль/л, если зависимость поверхностного натяжения от концентрации выражается уравнением Шишковского: σ = σ 0 – 16, 7·10-3 · ln(1 + 21, 5· c).
18 Константы уравнения изотермы адсорбции Фрейндлиха равны Кф=0, 012 и а =2. Найдите равновесную концентрацию уксусной кислоты в растворе, если 1 кг адсорбента поглощает 3, 05 моля уксусной кислоты.
Вариант 7 16 Золь ртути состоит из шариков диаметром 6∙ 10-6см. Чему равны: а) суммарная поверхность частиц; б) общее число частиц в растворе при дроблении 1г ртути? Плотность ртути 13, 546 г/см3.
17 Вычислите постоянную В уравнения Шишковского и величину предельной адсорбции на границе раздела фаз раствора масляной кислоты – воздух при 17°С, если площадь, занимаемая одной молекулой кислоты на поверхности раздела, равна 20, 5·10-20 м2.
18 На основании экспериментальных данных по адсорбции аскорбиновой кислоты углем при 298К графически определить постоянные в уравнении Фрейндлиха: с, моль/м3 0, 006 0, 025 0, 053 0, 111 Адсорбция, моль/кг 0, 44 0, 78 1, 04 1, 44
Вариант 8 16 Во сколько раз возрастет поверхность частиц в результате дробления кубиков серебра с длиной ребра 0, 5 см до частиц кубической формы с длиной ребра 5∙ 10-6см. Плотность серебра 10, 5 г/см3.
17 Предельная адсорбция пропионовой кислоты равна 4, 18∙ 10-6 моль/м2. Рассчитайте значение константы В уравнения Шишковского при стандартной температуре.
18 Активная поверхность активированного древесного угля достигает 1000 м2 на 1г угля. Рассчитайте, сколько фосгена (мг) поглотится поверхностью10 м2 угля, если 1 г угля адсорбирует 440 см3 газа. (Условия нормальные).
Вариант 9 16 Золь ртути состоит из шариков диаметром 2·10-7м. Рассчитать суммарную поверхность частиц и их общее число, если масса дисперсной фазы 2·10-4 кг, а плотность 13, 5·103 кг/м3.
17 Для водных растворов изоамилового спирта константы уравнения Шишковского: В = 21, 12∙ 10-3 Дж/м2; А = 42, 0 м3/кмоль. Поверхностное натяжение чистой воды при заданной температуре равно 72, 9∙ 10-3 Дж/м2. Определите поверхностное натяжение растворов концентраций 0, 012; 0, 013; 0, 032 кмоль/м3.
18 Активная поверхность 1 г силикагеля составляет 465 м2. Рассчитайте, сколько молекул брома поглощается 1 см2 поверхности адсорбента при адсорбции на 10 г силикагеля 5 мг брома. Вариант 10 16 Раствор коллоидной камфоры содержит в 1 см3 200 млн шариков камфоры диаметром около 10-4 см. Подсчитайте общую поверхность камфоры в 200 см3 такого раствора.
17 Определите величину адсорбции пропилового спирта на границе раздела водный раствор – воздух при 293 К и концентрации 0, 1 моль/л, если зависимость поверхностного натяжения от концентрации выражается уравнением Шишковского: σ = σ 0 – 14, 4·10-3 · ln(1 + 6, 6 · c).
18 Проверьте справедливость уравнения Фрейндлиха для адсорбции уксусной кислоты из её водного раствора углем по следующим экспериментальным данным: с, моль/м3 18 31 62 126 208 Адсорбция, моль/кг 0, 467 0, 624 0, 801 1, 110 1, 550 Найдите постоянные уравнения Фрейндлиха
|

 =
= 
 . (120)
. (120) , (121)
, (121) ; Г = Г∞
; Г = Г∞  ; (122)
; (122) θ =
θ =  ; (124)
; (124) ; (125)
; (125) ,
, . (126)
. (126) ,
,  ,
,  , -OH и др.) и неполярного углеводородного радикала, длина которого определяется числом атомов углерода в радикале и его строением. Такие молекулы называются дифильными. Их неполярный углеводородный радикал обращен в сторону менее полярной фазы адсорбционного слоя, а полярная функциональная группа – в сторону более полярной фазы.
, -OH и др.) и неполярного углеводородного радикала, длина которого определяется числом атомов углерода в радикале и его строением. Такие молекулы называются дифильными. Их неполярный углеводородный радикал обращен в сторону менее полярной фазы адсорбционного слоя, а полярная функциональная группа – в сторону более полярной фазы. (128).
(128). (129)
(129) , (130)
, (130) (131)
(131) .
.
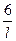 =
=  = 6·105 см-1.
= 6·105 см-1. = 0, 4831 см3.
= 0, 4831 см3.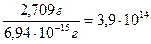 .
. .
. .
.
 моль/м2
моль/м2 , моль/г 0, 44 0, 78 1, 04 1, 44
, моль/г 0, 44 0, 78 1, 04 1, 44




