Электрическая проводимость растворов электролитов
Различают две основные группы проводников электрического тока: проводники I рода, электрическая проводимость которых обусловлена электронами (металлы, графит), и проводники II рода, обладающие ионной проводимостью (расплавы и растворы электролитов). В электрохимии рассматривают проводники II рода. Согласно теории Аррениуса, электролиты в водном растворе диссоциируют на заряженные частицы – ионы, которые и являются переносчиками электричества. При этом одни электролиты – сильные диссоциируют в растворе полностью, другие – слабые – лишь частично; доля распавшихся частиц – степень электролитической диссоциации (α) зависит от концентрации электролита и температуры. Величина, характеризующая способность веществ проводить электрический ток под действием внешнего электрического поля, называется электрической проводимостью. Электрическая проводимость (L) – величина, обратная электрическому сопротивлению проводника (R). Измеряется в сименсах (См): См = Ом-1. Так как R = то
где ρ – удельное сопротивление; Электрическая проводимость в растворах электролита зависит от числа ионов в объёме раствора между электродами и скорости их движения. Для оценки проводимости растворов и влияния на неё различных факторов применяют две величины: удельную (Χ) и молярную (λ) электрическую проводимость. Удельной электрической проводимостью (Χ) называют электропроводность раствора, находящегося между параллельными электродами площадью 1 см2, расположенными на расстоянии 1 см. Удельная электрическая проводимость измеряется в См·см-1 или См·м-1.Удельная электрическая проводимость раствора электролита зависит от природы электролита, концентрации раствора и температуры. Отношение расстояния между электродами l к их площади называют постоянной электролитической (кондуктометрической) ячейки
Подставляя (101) в уравнение (100), получаем: Χ = К L. (102) Величину К определяют экспериментально. Молярная электрическая проводимость – мера электрической проводимости всех ионов, образующихся при диссоциации 1 моля электролита при данной концентрации. Молярная электрическая проводимость равна электрической проводимости такого объёма ( V, см3) раствора, в котором содержится 1 моль растворённого электролита, причём электроды расположены на расстоянии 1 см друг от друга. Из определения удельной и молярной электрических проводимостей следует, что они связаны соотношением:
где С – концентрация, моль/дм3; λ – молярная электрическая проводимость, См·см2/моль; Χ – удельная электрическая проводимость, См/см. Поскольку электрическая проводимость объёма раствора электролита определяется количеством в этом объёме ионов, переносящих электричество, и скоростью их миграции, для молярной проводимости справедливо соотношение: λ = α F(U+ + U-), (104) где U+ и U- – абсолютные скорости движения ионов; α – степень диссоциации электролита; F – число Фарадея, т.е. количество электричества, которое несёт 1 моль однозарядных катионов или анионов: F = NA·e, где NA = 6·1023 – число Авогадро, e = 1, 6∙ 10-10 Кл – заряд электрона. При разбавлении раствора молярная электрическая проводимость как сильных, так и слабых электролитов возрастает; для слабых электролитов – вследствие увеличения степени диссоциации (α), для сильных электролитов – в результате повышения абсолютной скорости движения ионов (U+, U-). Предельное значение λ º, отвечающее молярной электрической проводимости гипотетического бесконечно разбавленного раствора, характеризующегося полной диссоциацией электролита и отсутствием сил электростатического взаимодействия между ионами, в соответствии с (104) можно выразить соотношением: λ º = F(U0+ + U0-). (105) Произведения FU0+ = λ Уравнение (105) можно представить в виде: λ º = λ Молярная электрическая проводимость электролита при бесконечном разбавлении (λ º) равна сумме предельных подвижностей анионов и катионов. Соотношение (106) было установлено Кольраушем и называется законом независимого движения ионов. Предельная подвижность ионов зависит только от природы растворителя и температуры; для многих ионов эта величина определена экспериментально и приводится в справочниках. Молярная электрическая проводимость слабых электролитов меньше, чем сильных,; так как даже при низких концентрациях степень диссоциации слабых электролитов мала (α ‹1). Следовательно, несмотря на то, что в объёме раствора, заключённого между электродами, содержится 1 моль электролита, переносчиков электрического тока – ионов в данном объёме меньше, чем в растворе сильного электролита. Повышение молярной электрической проводимости слабых электролитов при разбавлении растворов связано с увеличением степени диссоциации. Из уравнений (105) и (106) следует:
где Абсолютные скорости движения ионов в разбавленных растворах электролитов (U+, U-) и в бесконечно разбавленных (U0+, U0-) близки между собой (fλ =1), поэтому
Для слабых электролитов отношение молярной электропроводности раствора при данном разбавлении (λ) к молярной электропроводности при бесконечно большом разбавлении (λ º) характеризует истинную степень электролитической диссоциации. Степень диссоциации электролита в растворе заданной концентрации можно рассчитать, измерив молярную электрическую проводимость этого раствора и зная λ º. У слабых бинарных электролитов с разбавлением раствора увеличивается степень электролитической диссоциации и молярная электропроводность; константа же диссоциации при неизменной температуре остаётся постоянной величиной (закон разбавления Оствальда). Константа диссоциации Кдис, α, λ и концентрация (разбавление) подобных растворов связаны между собою следующими уравнениями: Кдис = Учитывая уравнение (108), Кдис = или Кдис = где V=1/C – разбавление раствора, л/г-экв. Для сильных электролитов, диссоциирующих полностью (α =1),
Уменьшение молярной электрической проводимости при переходе от бесконечно разбавленного раствора к растворам конечных концентраций у сильных электролитов связано только с уменьшением скоростей движения ионов. Сильные электролиты не подчиняются закону разбавления.
Пример 18. Для 0, 01н KCl удельное сопротивление ρ = 709, 22 Ом-1·см. Вычислите удельную(Χ) и молярную (λ) электрические проводимости. Решение. Удельную электрическую проводимость вычисляем по уравнению Χ = Молярная электрическая проводимость, согласно (103), можно выразить с помощью уравнения: λ = Пример 19. Вычислите молярную электрическую проводимость уксусной кислоты при бесконечно большом разбавлении при 298 К, если электрические проводимости HCl, CH3COONa, NaCl равны 0, 0426; 0, 0091; 0, 0126 См·см2/моль соответственно. Решение. Составляем систему уравнений согласно закону Кольрауша (106): λ HCl = λ H+ + λ Cl- = 0, 0426; (1) λ CH3COONa = λ NaCl = Согласно (106) складываем уравнения (1) и (2), вычитаем из них уравнение (3) и получаем: λ HCl + λ CH3COONa - λ NaCl = λ H+ +
Пример 20. Удельная электропроводность 0, 0109 н раствора NH4OH при 18º С 1, 02·10-4 См·см-1, а 0, 0219 н раствора 1, 5·10-4 См·см-1. Вычислить для указанных растворов степень диссоциации NH4OH и концентрации гидроксильных ионов. Проверить, насколько точно растворы NH4OH соответствуют закону разбавления. Решение. Вычисляем молярные электропроводности для первого и второго растворов по формуле (103):
По формуле (106), используя табличные данные, находим λ º λ º = Значения α определяем по формуле (108):
Вычисляем концентрацию ионов ОН- в растворах:
Зная α 1 и α 2, рассчитываем константу диссоциации NH4OH по уравнению (109) для двух растворов:
Величины
Вариант 1. 12. Электрическая проводимость 0, 01моль/дм3 раствора хлорида калия при 25º С равна 0, 0034 См. Удельная проводимость этого раствора 1, 41·10-3 См/см. Чему равна постоянная кондуктометрической ячейки? Вариант 2. 12. Сопротивление кондуктометрической ячейки, содержащей 0, 1 моль/дм3 раствора КСl, удельная электрическая проводимость которого равна 1, 29∙ 10-2 См/см, составляет 1, 16 Ом. Чему равна удельная проводимость этого раствора? Вариант 3. 12. Постоянная кондуктометрической ячейки К = 0, 41 см-1. Электрическая проводимость 0, 02 моль/дм3 раствора уксусной кислоты равна 5, 810-4 См. Чему равна молярная электрическая проводимость раствора? Вариант 4. 12. Вычислите молярную электрическую проводимость 0, 1 моль/дм3 раствора HCl, если удельная электрическая проводимость раствора 0, 039 См·см-1. Вариант 5. 12. Вычислите предельную молярную проводимость TlCl, если Вариант 6. 12. Удельная электрическая проводимость 0, 1 моль/дм3 раствора этиламина при 25º С равна 0, 0015 См∙ см-1. Предельная молярная проводимость 204 См·см2/моль. Найдите степень диссоциации и константу диссоциации этиламина. Вариант 7. 12. Молярная проводимость водного раствора амида азотной кислоты H2N2O2, с=0, 03 моль/дм3 равна 1, 007 См·см2/моль. Предельные подвижности ионов равны: Вариант 8. 12. Удельная электрическая проводимость 0, 001 моль/дм3 раствора уксусной кислоты равна 0, 492·10-4 См/см. Чему равна константа диссоциации уксусной кислоты? Вариант 9. 12. Произведение растворимости сульфата бария 1, 3·10-10. Чему равна удельная проводимость насыщенного раствора BaSO4, если удельная проводимость воды 1, 0·10-6 См/см? Вариант 10. 12. Постоянная ячейки 0, 41 см-1. Электрическая проводимость насыщенного раствора AgCl равна 8, 317·10-6 См. Удельная электрическая проводимость воды 1, 6·10-6 См/см. Считая молярную проводимость этого раствора равной предельной растворимости, найдите произведение растворимости AgCl.
|

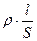 , (99)
, (99) , (100)
, (100) - удельная электрическая проводимость; S – площадь сечения проводника; l – длина проводника.
- удельная электрическая проводимость; S – площадь сечения проводника; l – длина проводника. . (101)
. (101) , (103)
, (103)
 и FU0- = λ
и FU0- = λ 
 , (107)
, (107) - коэффициент электрической проводимости, характеризующийся степенью торможения ионов.
- коэффициент электрической проводимости, характеризующийся степенью торможения ионов.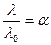 . (108)
. (108) . (109)
. (109) (110)
(110) , (111)
, (111) . (112)
. (112)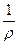 =
=  = 1, 41∙ 10-3 Ом-1·см-1 = См·см-1.
= 1, 41∙ 10-3 Ом-1·см-1 = См·см-1. 0, 0141 См·см2/моль.
0, 0141 См·см2/моль. 0, 0091; (2)
0, 0091; (2) = 0, 0126. (3)
= 0, 0126. (3) 0, 0426 + 0, 0091 – 0, 0126 = 0, 0391 См·см2/моль.
0, 0426 + 0, 0091 – 0, 0126 = 0, 0391 См·см2/моль. См·см2/моль,
См·см2/моль, См·см2/моль.
См·см2/моль. = 63, 6 + 174 = 237, 6 См·см2/моль.
= 63, 6 + 174 = 237, 6 См·см2/моль.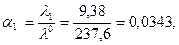


 .
.

 и
и 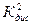 близки по значению. Следовательно, растворы NH4OH следуют закону разбавления.
близки по значению. Следовательно, растворы NH4OH следуют закону разбавления.

 См·см2/моль.
См·см2/моль. ,
, 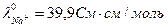 ,
,  . Определите константу диссоциации по уравнению: H2N2O2 ↔ H+ + HN2O
. Определите константу диссоциации по уравнению: H2N2O2 ↔ H+ + HN2O  .
.


