Третье правило: царство хаоса
...существует поразительное концептуальное изменение в осознании того, что даже без потрясений, контролируемых своей локальной рациональной логикой, развитие социальной системы может быть абсолютно непредсказуемым и что малейшее изменение в политике может стать причиной другого типа поведения. Mosekilde, Larsen & Sterman Это была темная и штормовая ночь. Грозовые тучи разрастались, сильные ливни сменялись мощными порывами ветра. Дождь лил стремительным потоком, на земле образовались струящиеся ручейки воды. На рассвете бледные лучи нового дня пробирались сквозь холодный воздух, и вода начала просачиваться в почву и испаряться. Компьютерная метеорологическая модель Эдварда Лоренца стала предметом повышенного внимания. После завершения работы над ней в 1960 году он проводил много времени в своей лаборатории в Массачусетском Технологическом институте, исследуя климатические модели. Принцип модели Лоренца на самом деле был очень прост: основываясь на вводимых снимках погодной картины, компьютер мог дать прогноз на небольшой период времени. Данные этого расчета становились основой для последующих вычислений и так далее. Компьютерная цепь вычислений могла воспроизводить 24 часа в минуту, после чего экран компьютера Лоренца становился сценой для драмы будущих событий: высокое давление, сменяющееся низким давлением, ураганы, вслед за которыми дул нежный ветерок, темные и штормовые ночи, после которых наступают ленивые летние дни. Модель Лоренца была больше, чем просто будоражащей. У нее был огромный потенциал. Что если однажды станет возможным предсказывать погоду на несколько месяцев вперед? Однако в тот зимний день 1961 года Лоренц сделал очень необычное и странное открытие. Он решил проверить предыдущее воспроизведение, на этот раз с более длинной последовательностью. Но вместо того, чтобы произвести все вычисления с начала, он попытался сократить процесс. Он ввел значения, полученные в прошлый раз, но начиная с середины цепочки. Затем он включил машину и вышел в коридор сделать себе чашечку кофе. В тот момент он совершенно не подозревал, что тем временем компьютерные итерации вели себя действительно очень странно. эффект бабочки Когда Лоренц вернулся, он очень удивился. Вычисления компьютера, которые должны были быть идентичны с предыдущей последовательностью, вообще выглядели неправильно. Они отклонялись все больше и больше и на два месяца вперед потеряли всякое сходство с первым воспроизведением. Сначала он приписал это ошибке компьютера, но вскоре он понял настоящую причину. Его отправные точки цепи вычислений имели трехдесятичную точность. Однако компьютерные расчеты велись с шестью десятичными знаками, что доказывало их существенную значимость. Его собственная интуиция подсказывала, что было бы разумным не придавать значения последним трем десятичным во вводимых данных, так как едва ли их могли зарегистрировать метеорологические измерительные инструменты: насколько важна была 1/1000 или еще меньше? Но в метеорологической компьютерной модели Лоренца эти десятичные дроби доказали свою огромную значимость. Открытие Лоренца не стало чем-то особенным для метеорологических прогнозов. Оно указало, в основном, на математический феномен, который ученые прежде никогда не замечали. Его сразу назвали " эффектом бабочки", так как реалистические имитации показали, что сложные вычисления системы сильно зависят от начальных значений, причем настолько сильно, что взмах крыла бабочки в Бразилии мог бы стать причиной возникновения торнадо в Техасе (Лоренц, 1979 год). Или, говоря финансовым языком: маленькая старушка, продающая несколько облигаций в Брюсселе, могла бы стать причиной краха в Японии! И выяснилось, что эта зависимость касалась не только сложных моделей: эффект бабочки можно было также обнаружить и в простых нелинейных моделях, демонстрирующих неустойчивость (рис. 4). детерминированный хаос Последствия этого открытия были революционными. Представьте себе, что поверхность Земли покрыта сетью метеостанций с трехдесятичной точностью, находящихся только в 30 см друг от друга, посылающих свои измерения в центральный компьютер каждую минуту. И предположите, что этот компьютер достаточно большой, чтобы вместить в себя совершенно правильную модель глобальных погодных моделей. Если бы даже и было так, то надежный прогноз погоды на месяц вперед сделать просто невозможно. Как раз вопреки своим первоначальным намерениям и ко всеобщему удивлению, Лоренц смог доказать, что невозможно и никогда не будет возможно давать долгосрочные прогнозы погоды. Эффект бабочки — один из элементов системы математических феноменов, с тех пор обобщенно названных термином " детерминированный хаос". Этот феномен охарактеризован Чера Л. Сайер-сом следующим образом (1989): " Процесс характеризуется детерминированным хаосом, если он генерирован полностью детерминированной системой1, возникающей как результат беспорядочно функционирующих рядов в стандартных временных диапазонах". Нас окружает хаос. Представим себе дымок сигареты в тихой комнате. Тысячи микроскопических частиц дыма поднимаются узкой колонкой, подталкиваемые горячим воздушным потоком. Затем внезапно колонка прерывается, заменившись турбулентными, постоянно меняющимися завихрениями дыма. Линейный поток трансформировался в хаос. И это происходит независимо от того, где вы находитесь. Или рассмотрим игру в футбол. Ни один, даже самый проницательный эксперт не сможет предугадать, где мяч окажется всего лишь через 10 секунд. Хаос наступает главным образом в отношениях, где присутствуют самопроизвольные усиливающиеся механизмы. Вообразите себе систему, в которой событие " А" приводит к событию " В", а событие " В" к событию " С". Если событие " С" затем воспроизводит событие " А", тогда в этом процессе есть простая цепь положительной обратной связи. Если мы попытаемся наметить в общих чертах взаимоотношения в экономике страны, как если бы это была метеорология, то вскоре столкнемся со сложными вариантами этих механизмов. Среди хорошо известных примеров есть так называемые эффекты мультипликации и акселерации, тезаврирование, самопроизвольное усиление ожиданий роста (" держаться наравне с Джонесесом"), увеличение потребностей в капитале из-за смещений во взаимоотношениях труда и капитала и т. д., — все вместе эти многочисленные цепочки обратных связей могут означать, что системы имеют не просто равновесие, а сами себя раскачивают или демонстрируют иные сложные движения. Каждая 'Детерминированная система (deterministic system) — система, выходы которой (результаты действия, конечные состояния и т.п.) однозначно определяются оказанными на нее управляющими воздействиями. Такие системы, по классификации Ст. Вира, могут быть простыми (например, оконная задвижка) и сложными (например, цифровая электронная вычислительная машина). Детерминированная система противопоставляется вероятностной системе, выходы которой лишь случайным образом, а не однозначно зависят от входов. — Прим. научн. ред.
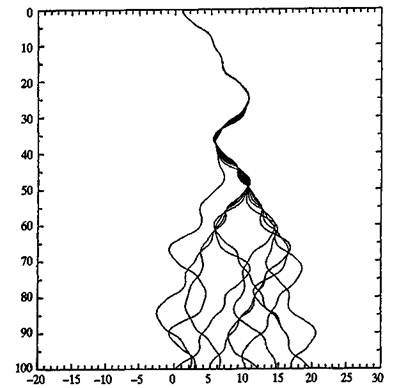
Рисунок 4 Эффект бабочки. График показывает математическое моделирование 11 объектов, скользящих вниз с неравномерными наклонами пиков и впадин, расположенных в синусоидальной модели. Длина наклона 100 метров. При моделировании объекты стартуют с одинаковым распределением точек, отдаленных друг от друга по горизонтали на 5 мм. Приблизительно через 30 метров их распределение уже в 20 метрах друг от друга. Интересный момент: график напоминает сигаретный дым, если его перевернуть наоборот. (Источник: Эдвард Н. Лоренц, Центр Метеорологии и Физической Океанографии, Кембридж, Массачусетс.) из этих положительно воздействующих цепей обратных связей может вносить свой вклад в самопроизвольно усиливающую природу экономического феномена, пока окончательно не будет заторможена другими механизмами. Чтобы правильно описать эти системы, необходимо применить нелинейную математику.
непредсказуемость, это как эндогенное Свойство Тем не менее экономическое моделирование традиционно строится на линейных моделях, основанных на функции равновесия. Эти модели показывают, как все элементы экономики непрерывно адаптируются ко всем другим элементам, но без каких-либо корректных оговорок, сделанных одновременно для многих положительных обратных связей. Когда контуры обратной связи объединяются, в основном, это бывают отрицательные, дестабилизирующие цепочки, то есть это вовсе не ведущие к устойчивости положительные контуры. Эти модели на практике функционируют очень вяло, что традиционно объясняется " стохастическими внешними беспокойствами", а также отсутствием точности в деталях модели. По этой причине результаты первых нелинейных компьютерных моделирований стали сильным шоком для всего академического мира. Внезапно все осознали, что линейные модели не только несовершенные, но и могут быть абсолютно неверными. Но самое важное заключалось в том, что даже теоретически правильные нелинейные модели могли привести к полной непредсказуемости, хотя они были детерминированными и структурированными по своему характеру. Это означает, что системы нарушались стохастическими внешними неупорядоченно-стями и непредсказуемость могла быть элементом собственной эндогенной природы макроэкономических систем. Как это может проявляться, показывает, например, феномен, называемый " раздвоение". тайна роберта Мэя Одним из первых, описавшим раздвоения, был австралийский биолог Роберт Мэй. В начале 70-х гг. Мэй разработал математическую модель развития в популяции рыб. Когда он вводил наименьшие значения для одной из переменных формулы — тренда репродукции рыб, — модель показывала определенную экологическую точку равновесия для определенных размеров популяции. Если популяция с самого начала находилась за пределами этой точки равновесия, она постепенно могла вернуться к этой точке посредством " подавляющих осцилляции". Этот результат был именно таким, каким и должен быть. Однако если Мэй вводил наивысшие значения, то размер популяции начинал постоянно колебаться то вверх, то вниз и никогда не мог достичь устойчивости. Таким образом, модель при отличающихся вводных данных демонстрировала прогнозы абсолютно разного характера: она демонстрировала хаос. Он нашел, что это очень загадочное явление, и стал изучать финальную модель для всех значений репродуктивного тренда. Результат оказался поразительным. При самых минимальных значениях популяция рыб естественным образом приходила к вымиранию. Если Мэй увеличивал значение репродуктивного тренда до определенного уровня, популяция могла выжить, и плавная кривая отражала ее уровни равновесия: чем выше значение репродуктивного тренда, тем сильнее оказывалась равновесная популяция. Но он обнаружил, что на определенном уровне плавная кривая неожиданно раздваивалась на две части. Это означало, что популяция могла колебаться между двумя различными уровнями равновесия. Такое явление названо " раздвоением" и полностью противоречило традиционным представлениям. После того как Мэй еще больше увеличил величину репродуктивного тренда, картина стала еще более странной: два уровня равновесия перешли уже в 4, затем в 8, 16, 32 и в конце концов привели к хаосу. Явление раздвоения имеет место не только в экологических моделях. В статье 1964 года " Проблема вывода климата из основного уравнения" (The Problem of Deducing the Climate from Governing Equations.), в Tellus, Лоренц представил теорию существования более чем одного равновесного климата для Земли. Факт состоял и состоит в том, что математические модели метеорологов изредка имеют возобновляющуюся тенденцию, внезапно начинающую колебаться от сегодняшнего климата до всемирного обледенения, — состояния, несомненно, такого же устойчивого, как и современная ситуация. Лоренц определял систему, обладающую более чем одним устойчивым состоянием равновесия, как " непереходную". Если он был прав, то известный ледниковый период мог быть последствием раздвоений или проявлением непереходных свойств, содержащихся в принадлежащей Богу формуле. Интересная мысль... Причина раздвоений в том, что существует внезапное и существенное изменение в преобладании различных контуров положительно воздействующих обратных связей. Возвращаясь к экономическим системам, подобная теоретическая структура выдвинута ученым Эрвином Лазло в 1987, который разделил параметры, способные воздействовать на преобладание тех или иных контуров в экономических системах, на три категории: • Технологические инновации • Конфликты и завоевания • Дисбаланс социального и экономического характера, На основе модели Лазло экономическая система может двигаться от простого состояния, например, от простых циклических колебаний до более сложных осцилляции, скажем, до двухуровневого равновесия. Такое происходит, когда параметр стимулируется выше определенного критического уровня. Представьте себе картель поставщиков товаров. При формировании картельной цены ценовые движения могут сдвигаться от уровня, определяемого осцилляциями традиционного экономического цикла, до величины, диктуемой изменчивыми колебаниями между годами, различающихся предельно высокими ценами (жесткость цен), и годами с предельно низкими ценами (упадок и конкуренция). Другими альтернативными вариантами равновесия одной и той же системы могут быть инфляция и гиперинфляция или, скажем, низкое и высокое налогообложение. Чем сильнее давление на критический параметр, тем больше возникнет раздвоений. Этот процесс нестабильных раздвоений называется каскадом Фейгенбаума3 (рис. 5), по имени математика того времени. В конечном счете, такой процесс ведет к хаосу. 3 Feigenbaum cascade.
Рисунок 5 Каскад Фейгенбаума. Диаграмма показывает, как простое равновесие множится все больше и больше, приводя, в конце концов, к хаотическому поведению. Раздвоения создаются простым уравнением: (Хп+1=г«Хп«(1-Хп)), где параметр R (горизонтальная ось) постепенно увеличивается от 1.68 до 4.00. (Источник: Е. Моускилд и Дж. Томсен, Датский Технический университет.) побережье британии Один из самых необычных элементов в исследовании неупорядоченных систем описан математиком Бенуа Мандельбротом, который, кстати, работал в группе исследований и развития компании IBM, где изучал все, что его интересовало. Мандельброт занимался изучением моделей и структур, в создании которых обычно участвовали хаотические и неупорядоченные естественные процессы. Это, конечно, то, чем занимаются большинство ученых, но что фундаментально отличало Мандельброта от других, так это его подход к перспективе и расстоянию. " Что является размерами любого объекта? " " Это, — говорит Мандельброт, — зависит от того, насколько далеко вы находитесь". С дальнего расстояния объект может уместиться всего в одной-единственной точке. С расстояния 1 метра объект занимает легко распознаваемое пространство. Но если мы будем придвигаться к нему все ближе и ближе, задача измерения этой области становится все более сложным делом. Шершавость, неровность и раздробленность, существующие на поверхности объекта, будут все более явными. Эта стало очевидным Мандельброту, когда у него возникла идея проверить длину границ, используя для этого разные карты. Он задал очень простой вопрос: " Какова длина побережья Англии? " Стандартный ответ из энциклопедии не устроил Мандельброта. Наоборот, он доказал, что побережье Британии или любое другое побережье бесконечно длинное. Фактор, определивший результат, — это с какого расстояния смотреть: в пределах самого узкого места любого залива всегда можно найти бухту, которая будет еще меньше. Таким образом, заливы внутри залива беспрестанно увеличивают общую длину побережья, которая в результате стремится к бесконечности. самомоделируемые системы Раздумывая над этими рекурсивными моделями4, заливами внутри заливов, Мандельброт назвал этот феномен " фрактально-стью". Что интересно в отношении фракталов, так это то, что они показывают, что система может постоянно повторять свои модели в различных масштабах или шкалах. Другими словами, является самомоделируемой. 4 Рекурсивная модель (recursive model) — динамическая модель, обладающая математическим свойством рекурсии, т. е. если даны, например, все переменные модели до момента (t— 1), то модель обеспечивает и получение одного за другим значений переменных для t, по ним для (t+1) и т. д. — Прим. научи, ред.
Побережье Британии, конечно, следует рассматривать, как неподвижный феномен. Но фракталы можно обнаружить и в динамических системах. Подходящим примером служит струнный инструмент, такой как гитара. Мы ударяем по струне, и она издает звук определенного тона. Но, когда мы двигаем палец вверх по грифу гитары, тональность увеличивается, и на двенадцатом ладу тоны начинают повторять самих себя, но уже в более высокой октаве. Мы сталкиваемся с явлением, в котором гармоническая система, по существу, повторяет саму себя на разных шкалах. Другими словами, такая система самомоделируемая. Или рассмотрим движения океана. На поверхности воды мы видим зыбь, нечто среднее между зыбью и волнами и, наконец, сами волны, каждая седьмая из которых часто больше остальных. Если трение ветра о воду приводит к таким явлениям, как зыбь, волны и " суперволны", можно говорить об этом феномене, как обладающем признаками фрактальности. Но это определение оправдывается только в том случае, если причиной подобного явления феномена был только ветер. Уникальность метода Мандельброта в том, что он не стремился изучать только это явление в пределах только вполне определенных границ (например, химиков не допускают к профессиональным исследованиям в области ядерной физики, хотя предмет изучения может быть описан химическими формулами), а пытался понять всю структуру в целом, рассматривая ее с точки зрения проявления эффекта бифуркации (процесса разветвления), который она производила. Точно таким же образом мы можем считать зыбь " крохотными волнами", хотя ее можно рассматривать и как всего лишь точки в целой рекурсивной структуре, возникшей в результате ветра. А как насчет волн, возникающих в результате приливоотливных явлений? Они также возникают благодаря фрактальному феномену? Хотя они возникают на поверхности Земли, но в действительности мы знаем, что причина их происхождения кроется в гравитационном воздействии Луны.
биржевые брокеры, сторонники теории хаоса и защитники теории случайных блужданий В университетах экономистов принято учить, что цены движутся беспорядочно. Затем они начинают работать на Уолл-стрит, где пытаются побить рынок. В чем же причина несогласованности?
Важно, что мы регулярно обнаруживаем экономические и финансовые явления, повторяющие самих себя на разных шкалах5. Некоторые из подобных явлений мы еще увидим в этой книге. Случайно вы наверняка можете обнаружить явление, которое, возможно, фрактальное, но в действительности столь же независимое, как морские волны. Одним из таких явлений можно назвать, например, экономические циклы. экономический и финансовый хаос На интуитивном уровне кажется верным, что равновесные экономические и финансовые системы — место проявления фрактальных явлений, эффектов бабочки и бифуркации. Или, другими словами, хаоса. Тем не менее экономистам-теоретикам потребовалось много времени, чтобы начать исследовать феномен хаоса. Но в начале 80-х годов XX столетия исследователи стали серьезнее заниматься изучением индикаторов экономического хаоса и в течение нескольких лет провели важные наблюдения (см. Ploeg, 1985, Chirella, 1986, Chen, 1986, Lorenz, 1987, Brock и Sayers, 1987, Rasmussen и Mosekilde, 1988). Чем дальше мы продвигались, тем больше обнаруживали признаки моделей, отражающих феномен хаоса в экономических системах. Теперь есть все признаки, что систематическая эндогенная долгосрочная непредсказуемость имеет место во многих экономических и финансовых системах. Даже там, где успокаивающие механизмы сильны или где хаос не возникает в интервале текущего параметрического интервала, импульсы от других хаотических подсистем способны значительно увеличить неопределенность. Образно говоря, проблему можно сравнить со срубленным деревом, проходящим через речную стремнину. Даже если бы мы знали все, что нужно знать о гидродинамике, воде и форме русла, мы бы никогда не смогли просчитать траекторию бревна дальше чем на несколько метров за один раз. Также было бы невозможно определить, откуда оно пришло, основываясь на его положении в данный момент времени. Подобная аналогия применима и к экономике. Следовательно, имеет место возрастающее осознание, что детерминированный хаос может иметь важное значение для более глубоко проникающих во временные пласты долгосрочных экономических прогнозов и что линейные модели дают весьма скудное представление о реальности. Понятно также, что динамические системы часто повторяют те же самые явления в различных масштабах, привнося, таким образом, больше сложностей в проблему прогнозирования.
s Также можно сказать: в различных масштабах, что более соответствует практике анализа поведения финансовых инструментов и рынков. Например, минутные интервалы, часовые, дневные, недельные, и т. д. — Прим. научн. ред.
вопрос размерности Важный аспект, имеющий отношение к хаосу, это " размерность". Это слово используется математиками для описания сложного поведения динамической системы. Несмотря на то, что размерность — математическое выражение, оно может быть объяснено (популярным языком), как обозначение числа прошлых наблюдений для предсказания последующего движения. Если система генерирует простые, синусоидальные осцилляции, предсказание становится пустячным делом и размерность равна нулю. Но если мы имеем дело с очень большим количеством взаимосвязанных обратных связей — положительных и отрицательных, — размерность резко возрастает, и вам понадобится много данных для " расшифровки" с помощью математики того, где вы находитесь в данный момент протекающего процесса. Когда размерность становится очень высокой, то даже очень большое количество исторических данных уже не поможет вам. Однако в этом случае невозможно доказать математическими методами присутствие неслучайной динамики. Как сказал Вильям А. Броук (1990), " на практике невозможно даже сказать, что образовало данные — детерминированная система высокого порядка или стохастическая система". Основываясь на современных положениях науки, становится понятным, что в реальности над финансовыми рынками господствуют сильные контуры обратной связи, создающие хаос высокого порядка (определяемый высокими значениями размерности), который математически расшифровать крайне сложно. Это частично доказывается математическими тестами, показывающими, что существует " нечто", не являющееся случайным, — даже просто невозможно точно выразить, что это именно такое. Частично это было доказано нашими периодически повторяющимися крахами, демонстрирующими присутствие сильных контуров обратной связи. понимание Экономики имеет важное значение Если детерминированный хаос — это то, что мы имеем, попытки аналитиков выполнить точные расчеты истинной величины начинают выглядеть, как попытки заниматься алхимией. Учитывая, что определение истинной стоимости акции исходит из того, что она приведенная стоимость всей будущей прибыли компании, то это просто смешно, если мы можем предвидеть только год, шесть месяцев или даже и того меньше. Возможно, нам следует вспомнить ранее приводимое описание поведения профессиональных экспертов, сделанное Кейн-сом: ...большинство из этих людей сильно беспокоит не создание первоклассных долгосрочных прогнозов возможного дохода от инвестирования на всем его протяжении, а предсказание изменений в условном базисе оценивания, которое бы шло чуть впереди основной публики. Вывод заключается не в том, что понимание экономики неуместно в отношении акции, — нет, никоим образом. Суть хаоса в том, что попытки предсказать длинные цепи событий или дать долгосрочные количественные прогнозы близки к абсурду. Хотя Кейнс вряд ли был хорошо знаком с позициями, на которых стоит нелинейная математика, в своей Основной теории он сделал следующий вывод: Инвестирование, основанное на долгосрочных ожиданиях, сегодня настолько сложно, что едва ли это осуществимое дело. Тот, кто решается на это, должен осознавать, что проведет намного больше напряженных дней и столкнется с намного большим риском, чем тот, кто пытается догадываться лучше толпы о том, как эта самая толпа будет себя вести. Кроме того, при равном уме с прочими он может допустить больше пагубных ошибок, нежели толпа в целом.
|