Кинетическое уравнение обратимой реакции первого порядка
Изменение концентрации исходных веществ и продуктов реакции во времени в случае протекания обратимой реакции можно показать на примере реакции первого порядка: А Û В. Пусть в начальный момент времени при t =0 концентрация исходного вещества А равняется C 0 A , а концентрация продукта В – C 0 B . Согласно закону действующих масс скорость прямой и обратной реакций будут описываться уравнениями
Скорость двухсторонней реакции определяется скоростью как прямого, так и обратного процессов:
Кинетические уравнения содержат три переменные: CA, CB и t. Для интегрирования одну необходимо исключить. Это можно сделать на основе материального баланса. Пусть к моменту времени t концентрации реагентов изменятся на величину x. Тогда CA = CA 0 – x, а CB = CB 0 + x,
Если обозначить
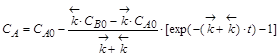 , ,
Изменение концентрации веществ А и В во времени приведено на рис.2.9.
Рис. 2.9. Изменение концентрации веществ А и В во времени при протекании обратимой реакции первого порядка А Û В.
Рис. 2.10. Изменение во времени скоростей прямой и обратной реакций первого порядка А Û В: По достижении равенства скоростей прямой и обратной реакции (рис. 2.10) концентрации исходного вещества и продукта изменяться не будут (в данном примере СА р=0, 167; СВ р=0, 833), система придет в состояние равновесия.
|

 ,
,  .
. ,
,  .
. ,
,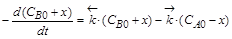 .
.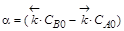 ,
,  , то можно преобразовать первое уравнение (или второе, результат будет одинаков) к виду
, то можно преобразовать первое уравнение (или второе, результат будет одинаков) к виду ,
,  ,
,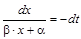 ,
,  ,
, при t =0 x =0
при t =0 x =0 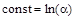 ,
, ,
,  ,
,  ,
, .
.

 ; C 0 A =1; C 0 B =0
; C 0 A =1; C 0 B =0




