Расчёт коэффициентов местных сопротивлений

Местные сопротивления представляют короткие участки трубопроводов, на которых скорости потока изменяются по значению или направлению в результате изменения размеров или формы сечения трубопровода, а также направления его продольной оси. Потери давления, возникающие при 'деформации потока в местных сопротивлениях, называются местными потерями давления Δ р _м.п. Они определяются по формуле Вейсбаха

 

(10)

где — безразмерный коэффициент местного сопротивления;

w — средняя скорость потока перед местным сопротивлением или после него (обычно берётся скорость за местным сопротивлением).

Значение коэффициента местных потерь в. общем случае зависит от пограничной геометрии (формы местного сопротивления, относительной шероховатости стенок, распределения скоростей в граничных сечениях потока перед местным сопротивлением и после него) и числа Рейнольдса.

Характер влияния числа Rе определяется режимом движения жидкости. При очень малых числах Rе (при ламинарном режиме) движение жидкости происходит без отрыва от стенок, а местные потери давления, обусловленные непосредственным действием сил вязкостного трения, оказываются пропорциональны первой степени скорости потока; коэффициент местного сопротивления при этих значениях числа Rе выражается формулой

, (11)

где В — коэффициент, зависящий от вида мест.ого сопротивления и степени стеснения потока (таблица 2)

Таблица 2 - Значения коэффициентов В для некоторых местных сопротивлений

Сопротивление	В	Сопротивление	В
Пробковый кран		Задвижка:
Вентиль		полное открытие п = 1
Колено		n = 0, 75
Угольник 135°	600;	n = 0, 5
Диафрагма: п = 0, 64		n = 0, 25
n = 0, 4		п — степень открытия
n = 0, 16

Примечание — Для арматуры при полном открытии и отсутствии необходимых данных о величине В можно принимать приближенно В = 500 _кв.

С увеличением числа Rе наряду с потерями на трение возникают потери, обусловленные отрывом потока и образованием вихревой зоны (переходная зона сопротивления). В переходной зоне коэффициент местного сопротивления определяется по формуле

, (12)

 

где _кв — коэффициент рассматриваемого местного сопротивления в квадратичной области.

При больших числах Rе основное значение приобретает вихреобразование, потери давления становятся пропорциональными квадрату скорости, т. к. коэффициент , перестаёт зависеть от числа Rе (так называемая квадратичная или автомодельная область сопротивления) и равен ζ кв (ζ = ζ кв).

Автомодельность (независимость) коэффициента местного сопротивления от числа Rе при резких переходах в трубопроводе наступает при Rе > 3000, а при плавных переходах — при Rе > 10000.

Влияние относительной шероховатости стенок проявляется в местных сопротивлениях только при больших значениях числа Rе (в квадратичной области сопротивления). Увеличение относительной шероховатости ведёт к возрастанию , которое существенно в тех случаях, когда местные потери давления обусловлены главным образом тормозящим действием стенок на поток, т. е. представляют потери на трение (колено, диффузор с малым углом раскрытия). Ниже приводятся значения коэффициента = _кв,.для некоторых местных сопротивлений (более подробные данные о местных сопротивлениях в напорных трубах см. [1, 2]). Все коэффициенты местных сопротивлений отнесены к динамическому давлению , определяемому по скорости за местным сопротивлением (кроме случаев, оговариваемых особо),

. (13)

Вентиль

Рисунок 1 — Вентиль

При полном открытии в зависимости от конструкции следует принимать:

а) для вентиля с прямым шпинделем по схеме рисунок 1 а

ζ _вен=3÷ 5, 5;

б) для вентиля с наклонным шпинделем по схеме рисунок 1 б

ζ _вен=1, 4÷ 1, 85.

Пробковый кран

Рисунок 2 — Пробковый кран

 

, град град
ζ КР	0, 05	0, 29	0, 75	1, 56	3, 1	5, 47	9, 68	17, 3	31, 2	52, 6

Таблица 3 — Значения коэффициентов для пробкового крана

Задвижка   Рисунок 3 — Задвижка	Коэффициент сопротивления зависит от отношения п (рисунок 3), т. е. от степени открытия (таблица 4)
Таблица 4 — Значения коэффициента ζ зад при различной степени открытия п   п 0 0 0, 125 0, 25 0, 375 0, 5 0, 625 0, 75 0, 875 ζ зад   0, 07 0, 26 0, 81 2, 06 5, 52 17, 0 97, 8
Диафрагма   Рисунок 4 Диафрагма	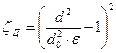Коэффициент сопротивления диафрагмы может быть определен по формуле , (14)   где коэффициент сжатия струи определяется по формуле   (15)
Внезапное расширение трубопровода Значение коэффициента ζ в.р.определяется по формуле
	, (16) где, как уже отмечалось, коэффициент потерь отнесен к динамическому давлению за сопротивлением, т. е. к квадрату скорости потока в большем сечении.
Рисунок 5 Внезапное расширение трубопровода   Внезапное сужение трубопровода
	Коэффициент сопротивления при внезапном сужении, трубопровода определяется по таблице 5 в зависимости от степени сжатия потока (отношение площадей сечения узкой и широкой трубы)
Рисунок 6 —- Внезапное сужение трубопровода

 

 

Таблица 5 — Значения коэффициента ζ _всв зависимости от степени сжатия п

ζ вс	0, 41	0, 40	0, 38	0, 36	0, 34	0, 30	0, 27	0, 20	0, 16	0, 1
п		0, 10	0, 20	0, 30	0, 40	0, 50	0, 60	0, 70	0, 80	0, 9