В механике грунтов при решении задач о распределении напряжений в основании используются существующие решения в теории упругости для разных видов нагрузок, приложенных к поверхности полупространства. Все нагрузки, действующие на основание, можно свести к трем видам: сосредоточенной силе, нагрузке, распределенной по ограниченной площадке, и нагрузке, распределенной по полосе.
Для определения напряжений от действия сосредоточенной силы можно воспользоваться формулой Ж. Буссинеска или Н.А. Цытовича [8. Гл. 3].
Для удобства расчета по формуле Цытовича, значения коэффициента К сведены в табл. П.1.3 приложения 1.
Используя формулу Н. А. Цытовича [8], можно найти  в любой точке основания при любой (в плане) площадке загружения. Для этого площадь фундамента разбивают на ряд малых площадок, и нагрузку, действующую на каждую из них, принимают за сосредоточенную силу
в любой точке основания при любой (в плане) площадке загружения. Для этого площадь фундамента разбивают на ряд малых площадок, и нагрузку, действующую на каждую из них, принимают за сосредоточенную силу  , приложенную в центре тяжести площадки. Напряжение в любой точке основания определяется методом суммирования. При определении напряжений от равномерно загруженной площадки любой формы в плане используется формула 2 приложения 2 СНиП 2.02.01-83*[1], и метод угловых точек.
, приложенную в центре тяжести площадки. Напряжение в любой точке основания определяется методом суммирования. При определении напряжений от равномерно загруженной площадки любой формы в плане используется формула 2 приложения 2 СНиП 2.02.01-83*[1], и метод угловых точек.
При определении напряжений в угловой точке прямоугольной или квадратной площадки пользуются формулой 3 приложения 2 СНиП 2.02.01-83* [1].
При определении напряжений в случае нагрузки, распределенной по закону треугольника, используется формула:
 , (2.1)
, (2.1)
где  - см. табл.П.1.4 приложения 1.
- см. табл.П.1.4 приложения 1.
Вертикальные давления на любой глубине по вертикали, проходящей через центр рассчитываемого фундамента, с учетом влияния соседних фундаментов,  определяется по формуле 5 СНиП 2.02.01-83* [1].
определяется по формуле 5 СНиП 2.02.01-83* [1].
 , (2.2)
, (2.2)
где  - давление от рассчитываемого фундамента;
- давление от рассчитываемого фундамента;
 - сумма давлений в точке «С» рассчитываемого фундамента от влияющих факторов, определяемая методом угловых точек;
- сумма давлений в точке «С» рассчитываемого фундамента от влияющих факторов, определяемая методом угловых точек;
K – число влияющих фундаментов.
При учете влияния нагрузки на полах вблизи фундамента можно считать, что при сплошной равномерной нагрузке на полах рассеивания напряжений от этой нагрузки с увеличением глубины не происходит и суммирование напряжения на глубине  составляет:
составляет:
 , (2.3)
, (2.3)
где  и g – соответственно напряжения от избыточного давления, передаваемого фундаментом и интенсивности равномерной нагрузки на полах.
и g – соответственно напряжения от избыточного давления, передаваемого фундаментом и интенсивности равномерной нагрузки на полах.
Если нагрузка на пол распределена по полосе шириной  равномерно или линейно по возрастающей, то нормальные напряжения
равномерно или линейно по возрастающей, то нормальные напряжения  на произвольной вертикали, расположенной на расстоянии
на произвольной вертикали, расположенной на расстоянии  от точки
от точки  (см. рис. 2.1) можно определить по формуле (2.1) или при равномерной нагрузке:
(см. рис. 2.1) можно определить по формуле (2.1) или при равномерной нагрузке:
 , (2.4)
, (2.4)
при треугольной нагрузке:
 , (2.5)
, (2.5)
Рис.2.1 Схема полосовой нагрузки на полы
а – равномерная нагрузка; б – треугольная
При определении давления грунта на трубопровод проложенной в траншее допускается пользоваться формулой:
 , (2.6)
, (2.6)
где  ;
;  ;
; 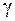 – удельный вес грунта; H – глубина засыпки.
– удельный вес грунта; H – глубина засыпки.
Пир закрытых проходах трубопровода (проколе)
 , (2.7)
, (2.7)
где 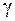 – удельный вес грунта засыпки (
– удельный вес грунта засыпки ( );
);
 – коэффициент трения для песков
– коэффициент трения для песков  , для связных
, для связных  ;
;
B – ширина разгружающего слоя;
 , (2.8)
, (2.8)
где R – радиус трубопровода.
2.1. Определить напряжение  в точке
в точке  под центром прямоугольной подошвы фундамента со сторонами
под центром прямоугольной подошвы фундамента со сторонами  м и
м и  м, нагруженного равномерно. Среднее давление под подошвой фундамента –
м, нагруженного равномерно. Среднее давление под подошвой фундамента –  МПа. Точка
МПа. Точка  лежит на глубине
лежит на глубине  м от подошвы фундамента.
м от подошвы фундамента.
2.2. Определить напряжение  в точке
в точке  находящейся на прямой, которая проходит через угол прямоугольного фундамента со сторонами
находящейся на прямой, которая проходит через угол прямоугольного фундамента со сторонами  м;
м;  м, на глубине
м, на глубине 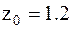 м от его подошвы. Давление под подошвой фундамента
м от его подошвы. Давление под подошвой фундамента  МПа.
МПа.
2.3. Определить напряжение  под центром круглого в плане фундамента
под центром круглого в плане фундамента  м при равномерном давлении
м при равномерном давлении  МПа в точке
МПа в точке  , находящейся на глубине
, находящейся на глубине  м ниже его подошвы.
м ниже его подошвы.
2.4. Определить напряжение  в точке
в точке  под центром фундамента с подошвой в виде правильного шестиугольника. Точка
под центром фундамента с подошвой в виде правильного шестиугольника. Точка  находится на глубине
находится на глубине  м от подошвы фундамента. Сторона шестигранного фундамента
м от подошвы фундамента. Сторона шестигранного фундамента  м, диаметр описанного круга
м, диаметр описанного круга  м, равномерно распределенное давление по подошве
м, равномерно распределенное давление по подошве  МПа.
МПа.
2.5. Определите напряжение  от сосредоточенной силы
от сосредоточенной силы  МН в точке М, находящейся на глубине
МН в точке М, находящейся на глубине  м и отстоящей от центральной оси на расстоянии
м и отстоящей от центральной оси на расстоянии  м.
м.
2.6. Определить напряжение  в точке М, расположенной на глубине 2 м от поверхности и на 1 м в сторону от оси, по которой действует сила
в точке М, расположенной на глубине 2 м от поверхности и на 1 м в сторону от оси, по которой действует сила  кН.
кН.
2.7. Определить вертикальное давление в грунте на глубине  м под центром прямоугольного в плане фундамента со сторонами подошвы
м под центром прямоугольного в плане фундамента со сторонами подошвы  м,
м,  м, если на фундамент передается центрально приложенная сила
м, если на фундамент передается центрально приложенная сила  кН.
кН.
2.8. Определить напряжение в точке  , находящейся на глубине 2 м от поверхности по оси, проходящей через центр загруженной квадратной площади, с учетом влияния загружения соседних площадей (рис. 2.2). Интенсивность равномерно распределенной нагрузки
, находящейся на глубине 2 м от поверхности по оси, проходящей через центр загруженной квадратной площади, с учетом влияния загружения соседних площадей (рис. 2.2). Интенсивность равномерно распределенной нагрузки  МПа
МПа
2.9. Определить напряжение  в точке
в точке  находящейся на глубине 4 м от поверхности по оси, проходящей через центр квадратного фундамента с учетом влияния соседнего фундамента (рис.2.3). Интенсивность равномерного давления по подошвам фундаментов
находящейся на глубине 4 м от поверхности по оси, проходящей через центр квадратного фундамента с учетом влияния соседнего фундамента (рис.2.3). Интенсивность равномерного давления по подошвам фундаментов  МПа.
МПа.
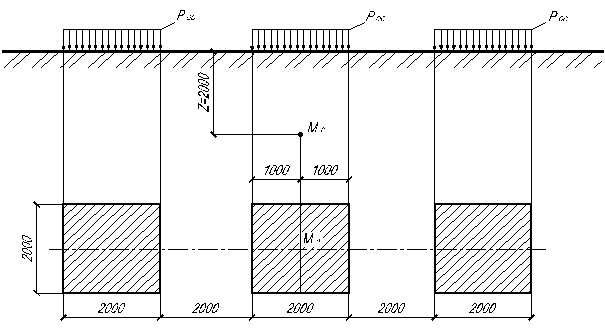
Рис. 2.2. Схема нагружения основания к задаче 2.8
2.10. Определить напряжение  в точке М, лежащей вне контура фундамента и имеющей координаты
в точке М, лежащей вне контура фундамента и имеющей координаты  м,
м,  м,
м,  м. Фундамент квадратной формы
м. Фундамент квадратной формы  м,
м,  м. Равномерное давление по подошве фундамента
м. Равномерное давление по подошве фундамента  МПа. Начало координат -в центре фундамента.
МПа. Начало координат -в центре фундамента.
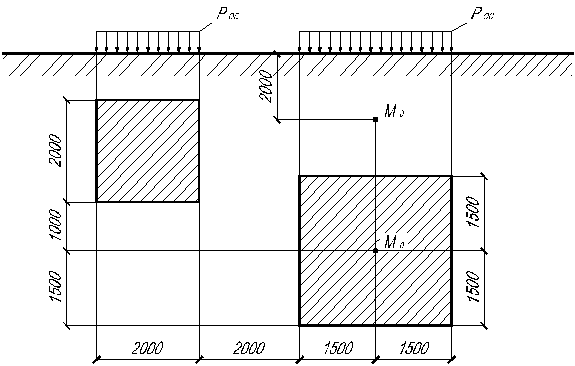
Рис. 2.3. Схема нагружения основания к задаче 2.9
2.11. Определить дополнительные напряжения  на глубине 2 м в точках
на глубине 2 м в точках  и
и  существующего фундамента под колонну от влияния проектируемого фундамента под оборудование (рис. 2.4.). Среднее давление по подошве проектируемого фундамента
существующего фундамента под колонну от влияния проектируемого фундамента под оборудование (рис. 2.4.). Среднее давление по подошве проектируемого фундамента  МПа.
МПа.
2.12. По треугольной площадке, имеющей равные стороны длиной 1 м, действует равномерно распределенная нагрузка 0.2 МПа. Найти напряжение  в точке М с координатами по отношению к одному из ее углов: x = 1 м, у = 0, 8 м, z= 1 м (рис. 2.5.)
в точке М с координатами по отношению к одному из ее углов: x = 1 м, у = 0, 8 м, z= 1 м (рис. 2.5.)
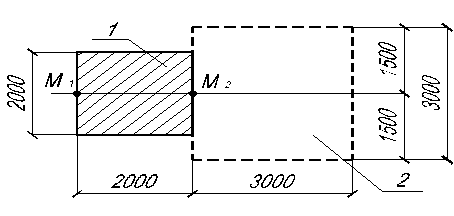
Рис. 2.4. Схема расположения фундаментов к задаче 2.11:
1-существующий фундамент; 2-проектируемый фундамент.
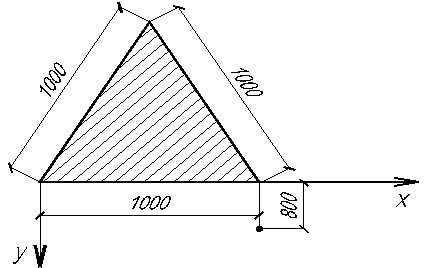
Рис. 2.5. Площадка загружения к задаче 2.12
2.13. Определить напряжения в точках  и
и  под центрами двух взаимно влияющих друг на друга фундаментов – ленточного, шириной
под центрами двух взаимно влияющих друг на друга фундаментов – ленточного, шириной  м, передающего на грунт нагрузку, изменяющуюся по закону треугольника
м, передающего на грунт нагрузку, изменяющуюся по закону треугольника  МПа, и стаканного с квадратной подошвой, размерами
МПа, и стаканного с квадратной подошвой, размерами  м, передающего равномерную
м, передающего равномерную
нагрузку  МПа. Глубина точек
МПа. Глубина точек  и
и  – z = 2 м. Схема расположения фундаментов представлена на рисунке 2.6.
– z = 2 м. Схема расположения фундаментов представлена на рисунке 2.6.
2.14. По условию предыдущей задачи определить напряжения в точках  и
и  на глубине z = 2м. (см. рис. 2.6).
на глубине z = 2м. (см. рис. 2.6).
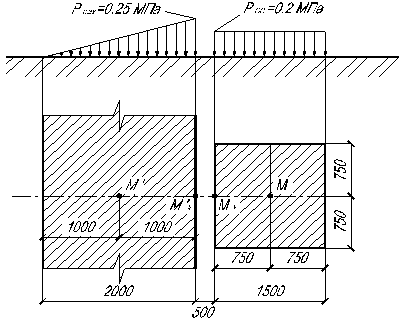
Рис. 2.6. Схема расположения фундаментов к задаче 2.13
2.15. Определить дополнительные  в точках
в точках  и
и  на глубине
на глубине  м основания фундамента тавровой формы при среднем равномерном давлении
м основания фундамента тавровой формы при среднем равномерном давлении  кПа (см. рис. 2.7.)
кПа (см. рис. 2.7.)
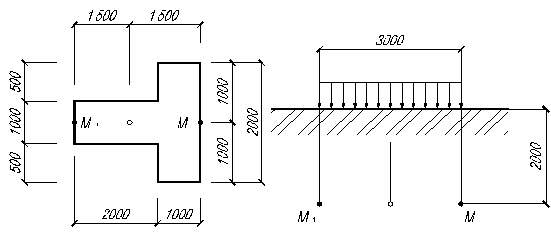
Рис. 2.7. Схема фундамента к задаче 2.15.
2.16. Определить напряжение  в точке Сна глубине 1 м от подошвы ленточного фундамента шириной м, глубиной заложения
в точке Сна глубине 1 м от подошвы ленточного фундамента шириной м, глубиной заложения  м и давлением по подошве
м и давлением по подошве  кПа с учетом равномерно распределенной по полосе шириной
кПа с учетом равномерно распределенной по полосе шириной  м нагрузки на
м нагрузки на
полы, интенсивностью  кПа. Расстояние от оси полосовой нагрузки до оси фундамента
кПа. Расстояние от оси полосовой нагрузки до оси фундамента  м.
м.
2.17.Определить напряжения  в точке С по условию задачи 2.16. приняв нагрузку на полы распределенную по закону треугольника с максимальной интенсивностью
в точке С по условию задачи 2.16. приняв нагрузку на полы распределенную по закону треугольника с максимальной интенсивностью  кПа и расстояние от дальнего края полосы до центра фундамента
кПа и расстояние от дальнего края полосы до центра фундамента  м.
м.
2.18. Определить напряжение  в точках
в точках  и
и  , расположенных по оси действующей горизонтальной силы
, расположенных по оси действующей горизонтальной силы  на глубине
на глубине  от поверхности земли согласно рис. 2.8.
от поверхности земли согласно рис. 2.8.
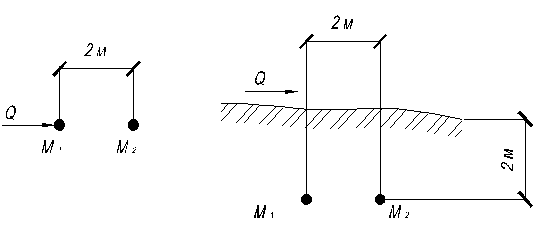
Рис. 2.8. Схема нагрузки на задачу 2.8.
2.19. Определить напряжение  ,
,  ,
,  для точек
для точек  и
и  на глубине 2 м от поверхности земли при нагружении равномерной полосовой нагрузкой шириной
на глубине 2 м от поверхности земли при нагружении равномерной полосовой нагрузкой шириной  м и интенсивностью
м и интенсивностью  кПа. Точка
кПа. Точка  расположена под центром полосовой нагрузки. Точка
расположена под центром полосовой нагрузки. Точка  за пределами полосы на расстоянии 3 м от ее оси.
за пределами полосы на расстоянии 3 м от ее оси.
2.20. Используя условия задачи 2.19 определить главные напряжения  и
и  в указанных точках
в указанных точках  и
и  .
.
2.21. Определить природные давления  на глубине
на глубине  м для следующих грунтовых условий:
м для следующих грунтовых условий:
Слой 1 – насыпь неслежавшаяся  ; h = 1 м
; h = 1 м
Слой 2 – чернозем  ; h = 0.7 м
; h = 0.7 м
Слой 3 – суглинок  ; h = 2 м
; h = 2 м
Слой 4 – песок крупный  ;
;  ;
;  ; h = 4 м
; h = 4 м
Слой 5 – глина  ;
;  ; h = 4 м
; h = 4 м
2.22. Построить эпюру дополнительных давлений  для квадратного фундамента шириной
для квадратного фундамента шириной  м со средним давлением по подошве
м со средним давлением по подошве  кПа и глубиной заложения
кПа и глубиной заложения  м с использованием геологических условий задачи 2.21.
м с использованием геологических условий задачи 2.21.
2.23. Построить эпюру дополнительных давлений  под подошвой существующего ленточного фундамента глубиной заполнения
под подошвой существующего ленточного фундамента глубиной заполнения  м и шириной
м и шириной  м от влияния пристроенного фундамента (
м от влияния пристроенного фундамента ( м,
м,  м,
м,  кПа) и равномерной нагрузкой на полы существующего здания интенсивностью
кПа) и равномерной нагрузкой на полы существующего здания интенсивностью  кПа согласно рис. 2.9., удельный вес грунта принят
кПа согласно рис. 2.9., удельный вес грунта принят  .
.
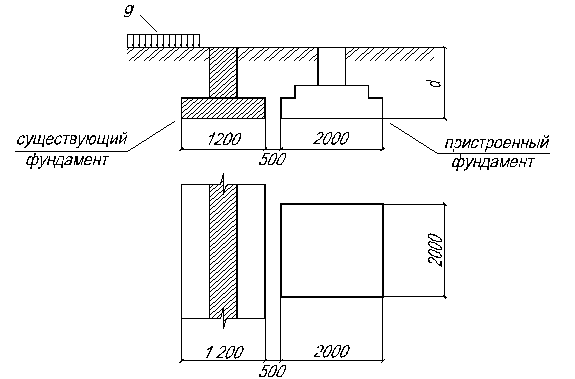
Рис. 2.9. Схема фундамента к задаче 2.23.
2.24. Определить интенсивность давления  на перекрытие воздуховода при глубине перекрытия воздуховода – 2 м от поверхности земли. Грунт – песок
на перекрытие воздуховода при глубине перекрытия воздуховода – 2 м от поверхности земли. Грунт – песок  .
.
2.25. Определить интенсивность давления  на перекрытие полупроходного канала под автодорогой. Глубина засыпки – 0.7 м, грунт – песок
на перекрытие полупроходного канала под автодорогой. Глубина засыпки – 0.7 м, грунт – песок  , вертикальная нагрузка от двухосных автомобилей
, вертикальная нагрузка от двухосных автомобилей  .
.
2.26. Определить вертикальные и горизонтальные давления грунта от засыпки проходного канала высотой 2 м, проложенного под дорогой. Глубина засыпки – 2 м, давление от транспортных средств принять  МПа. Грунт - песок
МПа. Грунт - песок  .
.
2.27. Определить давление на трубопровод радиусом  м уложенный в траншею на глубину 2 м, грунт - песок
м уложенный в траншею на глубину 2 м, грунт - песок  ,
, 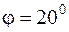
2.28. Определить давление на трубопровод диаметром 1 м устроенный прокопом на глубине 2 м в связных грунтах  ;
;  ;
;  кПа.
кПа.

 в любой точке основания при любой (в плане) площадке загружения. Для этого площадь фундамента разбивают на ряд малых площадок, и нагрузку, действующую на каждую из них, принимают за сосредоточенную силу
в любой точке основания при любой (в плане) площадке загружения. Для этого площадь фундамента разбивают на ряд малых площадок, и нагрузку, действующую на каждую из них, принимают за сосредоточенную силу  , приложенную в центре тяжести площадки. Напряжение в любой точке основания определяется методом суммирования. При определении напряжений от равномерно загруженной площадки любой формы в плане используется формула 2 приложения 2 СНиП 2.02.01-83*[1], и метод угловых точек.
, приложенную в центре тяжести площадки. Напряжение в любой точке основания определяется методом суммирования. При определении напряжений от равномерно загруженной площадки любой формы в плане используется формула 2 приложения 2 СНиП 2.02.01-83*[1], и метод угловых точек. , (2.1)
, (2.1) - см. табл.П.1.4 приложения 1.
- см. табл.П.1.4 приложения 1. определяется по формуле 5 СНиП 2.02.01-83* [1].
определяется по формуле 5 СНиП 2.02.01-83* [1]. , (2.2)
, (2.2) - давление от рассчитываемого фундамента;
- давление от рассчитываемого фундамента; - сумма давлений в точке «С» рассчитываемого фундамента от влияющих факторов, определяемая методом угловых точек;
- сумма давлений в точке «С» рассчитываемого фундамента от влияющих факторов, определяемая методом угловых точек; составляет:
составляет: , (2.3)
, (2.3) и g – соответственно напряжения от избыточного давления, передаваемого фундаментом и интенсивности равномерной нагрузки на полах.
и g – соответственно напряжения от избыточного давления, передаваемого фундаментом и интенсивности равномерной нагрузки на полах. равномерно или линейно по возрастающей, то нормальные напряжения
равномерно или линейно по возрастающей, то нормальные напряжения  на произвольной вертикали, расположенной на расстоянии
на произвольной вертикали, расположенной на расстоянии  от точки
от точки  (см. рис. 2.1) можно определить по формуле (2.1) или при равномерной нагрузке:
(см. рис. 2.1) можно определить по формуле (2.1) или при равномерной нагрузке: , (2.4)
, (2.4) , (2.5)
, (2.5)

 , (2.6)
, (2.6) ;
;  ;
; 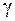 – удельный вес грунта; H – глубина засыпки.
– удельный вес грунта; H – глубина засыпки. , (2.7)
, (2.7) );
); – коэффициент трения для песков
– коэффициент трения для песков  , для связных
, для связных  ;
; , (2.8)
, (2.8) под центром прямоугольной подошвы фундамента со сторонами
под центром прямоугольной подошвы фундамента со сторонами  м и
м и  м, нагруженного равномерно. Среднее давление под подошвой фундамента –
м, нагруженного равномерно. Среднее давление под подошвой фундамента –  МПа. Точка
МПа. Точка  м от подошвы фундамента.
м от подошвы фундамента. м, на глубине
м, на глубине 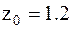 м от его подошвы. Давление под подошвой фундамента
м от его подошвы. Давление под подошвой фундамента  МПа.
МПа. м при равномерном давлении
м при равномерном давлении  , находящейся на глубине
, находящейся на глубине  м ниже его подошвы.
м ниже его подошвы. м от подошвы фундамента. Сторона шестигранного фундамента
м от подошвы фундамента. Сторона шестигранного фундамента  м, диаметр описанного круга
м, диаметр описанного круга  м, равномерно распределенное давление по подошве
м, равномерно распределенное давление по подошве  МПа.
МПа. МН в точке М, находящейся на глубине
МН в точке М, находящейся на глубине  м и отстоящей от центральной оси на расстоянии
м и отстоящей от центральной оси на расстоянии  м.
м. кН.
кН. м,
м,  кН.
кН.
 м,
м,  м,
м,  м. Фундамент квадратной формы
м. Фундамент квадратной формы  м. Равномерное давление по подошве фундамента
м. Равномерное давление по подошве фундамента 
 и
и  МПа.
МПа.

 и
и  под центрами двух взаимно влияющих друг на друга фундаментов – ленточного, шириной
под центрами двух взаимно влияющих друг на друга фундаментов – ленточного, шириной  МПа, и стаканного с квадратной подошвой, размерами
МПа, и стаканного с квадратной подошвой, размерами  м, передающего равномерную
м, передающего равномерную на глубине z = 2м. (см. рис. 2.6).
на глубине z = 2м. (см. рис. 2.6).
 кПа (см. рис. 2.7.)
кПа (см. рис. 2.7.)
 м и давлением по подошве
м и давлением по подошве  кПа с учетом равномерно распределенной по полосе шириной
кПа с учетом равномерно распределенной по полосе шириной  м нагрузки на
м нагрузки на кПа. Расстояние от оси полосовой нагрузки до оси фундамента
кПа. Расстояние от оси полосовой нагрузки до оси фундамента  м.
м. кПа и расстояние от дальнего края полосы до центра фундамента
кПа и расстояние от дальнего края полосы до центра фундамента  м.
м. в точках
в точках  , расположенных по оси действующей горизонтальной силы
, расположенных по оси действующей горизонтальной силы  на глубине
на глубине  от поверхности земли согласно рис. 2.8.
от поверхности земли согласно рис. 2.8.
 для точек
для точек  м и интенсивностью
м и интенсивностью  кПа. Точка
кПа. Точка  за пределами полосы на расстоянии 3 м от ее оси.
за пределами полосы на расстоянии 3 м от ее оси. и
и  в указанных точках
в указанных точках  на глубине
на глубине  м для следующих грунтовых условий:
м для следующих грунтовых условий: ; h = 1 м
; h = 1 м ; h = 0.7 м
; h = 0.7 м ; h = 2 м
; h = 2 м ;
;  ; h = 4 м
; h = 4 м ;
;  ; h = 4 м
; h = 4 м для квадратного фундамента шириной
для квадратного фундамента шириной  кПа и глубиной заложения
кПа и глубиной заложения  м от влияния пристроенного фундамента (
м от влияния пристроенного фундамента ( м,
м,  м,
м,  кПа согласно рис. 2.9., удельный вес грунта принят
кПа согласно рис. 2.9., удельный вес грунта принят 
 .
. МПа. Грунт - песок
МПа. Грунт - песок  м уложенный в траншею на глубину 2 м, грунт - песок
м уложенный в траншею на глубину 2 м, грунт - песок 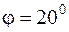
 ;
;  кПа.
кПа.


