Динамика материальной точки и тела, движущегося поступательно
Уравнение движения материальной точки (второй закон Ньютона) в векторной форме:
где в координатной (скалярной) форме:
или
где под знаком суммы стоят проекции сил Сила упругости –
где k – коэффициент упругости (в случае пружины жесткости); x – абсолютная деформация. Сила гравитационного взаимодействия –
где G – гравитационная постоянная; Сила трения скольжения –
где f – коэффициент трения скольжения; N – сила нормального давления. Значения координат центра масс системы материальных точек –
где Закон сохранения импульса –
где n – число материальных точек или тел, входящих в систему. Работа, совершаемая постоянной силой, –
где Работа, совершаемая переменной силой, –
причем интегрирование ведётся вдоль траектории, обозначаемой L. Средняя мощность за интервал времени
Мгновенная мощность –
где dA – работа, совершаемая за промежуток времени dt. Кинетическая энергия материальной точки (или тела, движущегося поступательно) –
Соотношение потенциальной энергии тела и силы, действующей на него в данной точке поля, –
где
Потенциальная энергия упругодеформированного тела (сжатой или растянутой пружины) –
Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массами
Потенциальная энергия тела, находящегося в однородном поле силы тяжести, –
где h – высота нахождения тела над уровнем, принятым за нулевой для отсчёта потенциальной энергии. Эта формула справедлива при условии, что h< < R, где R – радиус Земли. Закон сохранения энергии в механике выполняется в замкнутой системе, в которой действуют только консервативные силы, и записывается в виде
Применив законы сохранения энергии и импульса в случае прямого центрального удара шаров, получаем формулу скорости абсолютно неупругих шаров
и формулы скорости абсолютно упругих шаров после удара:
где
|

 , или
, или  ,
, - геометрическая сумма сил, действующих на материальную точку; m – масса;
- геометрическая сумма сил, действующих на материальную точку; m – масса;  – ускорение;
– ускорение;  – импульс; n – число сил, действующих на точку;
– импульс; n – число сил, действующих на точку; ;
;  ;
;  ,
, ;
;  ;
;  ,
, на соответствующие оси координат.
на соответствующие оси координат.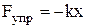 ,
, ,
, и
и 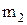 - массы взаимодействующих тел, рассматриваемых как материальные точки; r – расстояние между ними.
- массы взаимодействующих тел, рассматриваемых как материальные точки; r – расстояние между ними. ,
, ;
;  ;
;  ,
, – масса
– масса  - й точки;
- й точки; 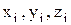 – координаты точки.
– координаты точки.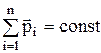 , или
, или  ,
,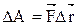 , или
, или  ,
, – угол между направлениями векторов силы
– угол между направлениями векторов силы  и перемещения
и перемещения 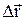 .
. ,
, –
–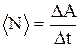 .
. , или
, или  ,
,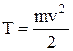 , или
, или  .
. , или
, или  ,
, – единичные векторы (орты). В частном случае, когда поле сил обладает сферической симметрией (например, гравитационное), –
– единичные векторы (орты). В частном случае, когда поле сил обладает сферической симметрией (например, гравитационное), – .
.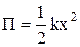 .
.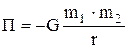 .
. ,
,
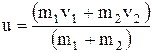
 ,
, ,
, и
и 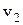 – скорости шаров до удара;
– скорости шаров до удара; 


