Кинематика
Положение материальной точки в пространстве задаётся радиус-вектором
где Кинематические уравнения движения (в координатной форме) таковы:
где t – время. Средняя скорость – < где Средняя путевая скорость – < где Мгновенная скорость –
где Абсолютное значение скорости –
Ускорение –
где Абсолютное значение ускорения –
При криволинейном движении ускорение можно представить как сумму нормальной
Кинематическое уравнение равнопеременного движения материальной точки вдоль оси x:
где При равномерном движении
Кинематическое уравнение равнопеременного движения (a=const) вдоль оси x:
где Скорость точки при равномерном движении:
Кинематическое уравнение вращательного движения:
Средняя угловая скорость –
где Мгновенная угловая скорость –
Угловое ускорение –
Кинематическое уравнение равномерного вращения –
где
Частота вращения –
где N – число оборотов, совершаемых телом за время t; Т – период вращения (время одного полного оборота). Кинематическое уравнение равнопеременного вращения (ε =const):
где Угловая скорость тела при равнопеременном вращении:
Связь между линейными и угловыми величинами, характеризующими вращение материальной точки, выражается следующими формулами:
|

 :
: ,
, – единичные векторы направлений (орты); x, y, z – координаты точки.
– единичные векторы направлений (орты); x, y, z – координаты точки. ;
;  ;
;  ,
, > =
> =  ,
,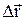 – перемещение материальной точки за интервал времени
– перемещение материальной точки за интервал времени  .
. > =
> =  ,
, - путь, пройденный точкой за интервал времени
- путь, пройденный точкой за интервал времени  ,
, – проекции скорости
– проекции скорости  .
. ,
, ;
;  ;
;  – проекции ускорения
– проекции ускорения  на оси координат.
на оси координат. .
. и тангенциальной
и тангенциальной  составляющих, см. рис 1
составляющих, см. рис 1
 Рис. 1.
Рис. 1.
 ;
;  ;
;  ,
где R – радиус кривизны в данной точке траектории.
,
где R – радиус кривизны в данной точке траектории.
 ,
, - начальная координата; t – время.
- начальная координата; t – время.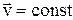 ;
; 
 – начальная скорость; t – время.
– начальная скорость; t – время. .
. .
. ,
, - изменение угла поворота за интервал времени
- изменение угла поворота за интервал времени  .
. .
. ,
, - угловое перемещение; t – время. При равномерном вращении
- угловое перемещение; t – время. При равномерном вращении и ε =0.
и ε =0. , или
, или  ,
, ,
, - начальная скорость; t – время.
- начальная скорость; t – время. .
. (где
(где  – угол поворота тела) – длина пути, пройденного точкой по дуге окружности радиусом R;
– угол поворота тела) – длина пути, пройденного точкой по дуге окружности радиусом R; ,
,  – линейная скорость точки;
– линейная скорость точки; ,
,  – тангенциальное ускорение точки;
– тангенциальное ускорение точки; – нормальное ускорение точки.
– нормальное ускорение точки.


