Управление запасами
Задача поиска оптимальной величины закупаемой партии и количество заказов в плановом периоде при минимизации издержек по складированию и обслуживанию закупаемых материалов выглядит следующим образом. Пусть для предприятия необходим на текущий плановый период (год) некоторый материальный ресурс в объеме – М по цене за единицу ресурса – Ц. Предполагаемое количество поставляемых партий ресурса – N. Издержки по складированию материальных ресурсов (I) исчисляются в процентах от величины среднегодового запаса материальных ресурсов. Издержки по обслуживанию закупаемой партии материального ресурса – Оn. Если годовая потребность в ресурсе удовлетворяется за счет одной поставки, то среднегодовое наличие ресурса на складе М/2 (М – на начало года и 0 на конец года). При двух поставках ресурса в течение года среднегодовой запас на складе данного ресурса – M/4, т.е. при N поставках среднегодовое значение материального ресурса на складе M/2N. Годовые затраты по складированию материальных ресурсов при N поставках: (M ´ Ц ´ I)/2N Затраты по обслуживанию N поставок – N ´ Оn. Общие затраты (См) при N поставках материального ресурса: Cм= (M ´ Ц ´ I)/2N + N ´ Оn Оптимальное количество партий можно найти, продифференцировав функцию совокупных издержек Cм по N dCм/dN = ‑ (М ´ Ц ´ I ´ N-2)/2 + Оn, При оптимальном значении dCм/dN = 0 получим: Оn = (М ´ Ц ´ I ´ N-2)/2, N-2= (2 ´ Оn)/ (М ´ Ц ´ I), отсюда Величина оптимальной закупаемой партии материального ресурса (Q):
|

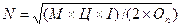 .
. .
.


