Лабораторная работа № 4. Программирование алгоритмов сортировки
Цель работы: приобретение навыков реализации программ сортировки данных. Краткие теоретические сведения Сортировкой или упорядочиванием списка элементов называется расположение этих элементов по возрастанию или убыванию, согласно определенному линейному отношению порядка (для определенности, нижеприведенные алгоритмы предполагают сортировку по возрастанию). Процесс сортировки, проводимый любым методом, состоит из нескольких циклов, в каждом из которых осуществляется просмотр всей последовательности и производятся определенные операции с ее элементами. Один цикл обработки называется проходом. Элементы обычно называют записями. Записи содержат ключи, по значениям которых осуществляется сортировка. При внутренней сортировке все сортируемые данные помещаются в оперативную память компьютера. Внешняя сортировка подразумевает перемещение больших блоков данных от устройств внешнего хранения информации к оперативной памяти и обратно. Метод выбора. При сортировке массива a[1], a[2],..., a[n] методом простого выбора среди всех элементов находится элемент с наименьшим значением a[i], и a[1] и a[i] обмениваются значениями. Затем этот процесс повторяется для получаемых подмассивов a[2], a[3],..., a[n],... a[j], a[j+1],..., a[n] до тех пор, пока мы не дойдем до подмассива a[n], содержащего к этому моменту наибольшее значение. Работа алгоритма иллюстрируется примером в таблице 1.
Таблица 1 Пример сортировки простым выбором
Метод обмена. Простая обменная сортировка (" метод пузырька") для массива a[1], a[2],..., a[n] работает следующим образом. Начиная с конца массива, сравниваются два соседних элемента (a[n] и a[n-1]). Если выполняется условие a[n-1] > a[n], то значения элементов меняются местами. Процесс продолжается для a[n-1] и a[n-2] и т.д., пока не будет произведено сравнение a[2] и a[1]. Понятно, что после этого на месте a[1] окажется элемент массива с наименьшим значением. На втором шаге процесс повторяется, но последними сравниваются a[3] и a[2]. На последнем шаге будут сравниваться только текущие значения a[n] и a[n-1]. Пример сортировки методом пузырька показан в таблице 2. Таблица 2 Пример сортировки методом пузырька
Сортировка разделением (Quicksort). Основная идея алгоритма состоит в том, что случайным образом выбирается некоторый элемент массива x, после чего массив просматривается слева, пока не встретится элемент a[i] такой, что a[i] > x, а затем массив просматривается справа, пока не встретится элемент a[j] такой, что a[j] < x. Эти два элемента меняются местами, и процесс просмотра, сравнения и обмена продолжается, пока мы не дойдем до элемента x. В результате массив окажется разбитым на две части - левую, в которой значения ключей будут меньше x, и правую со значениями ключей, большими x. Далее процесс рекурсивно продолжается для левой и правой частей массива до тех пор, пока каждая часть не будет содержать в точности один элемент. Рекурсию можно заменить итерациями, если запоминать соответствующие индексы массива. Проследим этот процесс на примере стандартного массива (таблица 3). Таблица 3 Пример быстрой сортировки
Сортировка включением. Одним из наиболее простых и естественных методов внутренней сортировки является сортировка с простыми включениями. Пусть имеется массив ключей a[1], a[2],..., a[n]. Для каждого элемента массива, начиная со второго, производится сравнение с элементами с меньшим индексом (элемент a[i] последовательно сравнивается с элементами a[i-1], a[i-2]...) и до тех пор, пока для очередного элемента a[j] выполняется соотношение a[j] > a[i], a[i] и a[j] меняются местами. Если удается встретить такой элемент a[j], что a[j] < = a[i], или если достигнута нижняя граница массива, производится переход к обработке элемента a[i+1] (пока не будет достигнута верхняя граница массива). Дальнейшим развитием метода сортировки с включениями является сортировка методом Шелла, называемая сортировкой включениями с уменьшающимся расстоянием. Для массива с 2n элементами алгоритм работает следующим образом. На первой фазе производится сортировка включением всех пар элементов массива, расстояние между которыми есть 2(n-1). На второй фазе производится сортировка включением элементов полученного массива, расстояние между которыми есть 2(n-2). И так далее, пока мы не дойдем до фазы с расстоянием между элементами, равным единице, и не выполним завершающую сортировку с включениями. Применение метода Шелла показано в таблице 4. Таблица 4 Пример сортировки методом Шелла
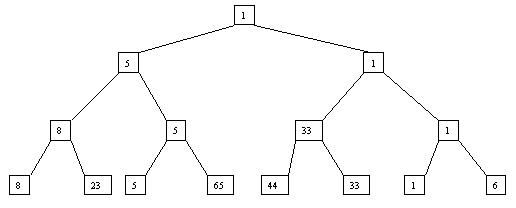
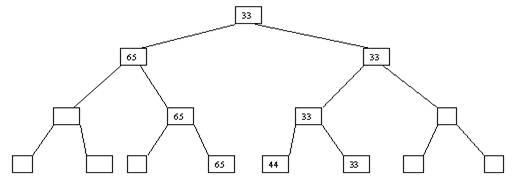
Сортировка с помощью дерева (Heapsort). Простой метод сортировки с помощью дерева характеризуется построением двоичного дерева сравнения ключей. Построение дерева начинается с листьев, которые содержат все элементы массива. Из каждой соседней пары выбирается наименьший элемент, и эти элементы образуют следующий (ближе к корню уровень дерева). Из каждой соседней пары выбирается наименьший элемент и т.д., пока не будет построен корень, содержащий наименьший элемент массива. Двоичное дерево сравнения для массива показано на рисунке 1.
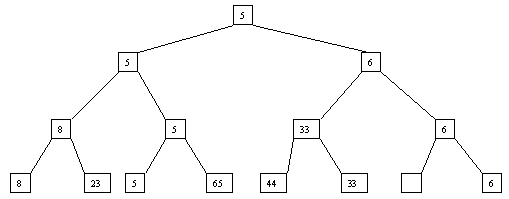
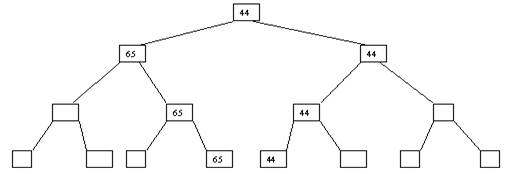
Рис. 1. Исходное дерево На данном шаге уже получено наименьшее значение элементов массива. Для того, чтобы получить следующий по величине элемент, спустимся от корня по пути, ведущему к листу с наименьшим значением. В этой листовой вершине проставляется фиктивный ключ с " бесконечно большим" значением, а во все промежуточные узлы, занимавшиеся наименьшим элементом, заносится наименьшее значение из узлов - непосредственных потомков (рис. 2).
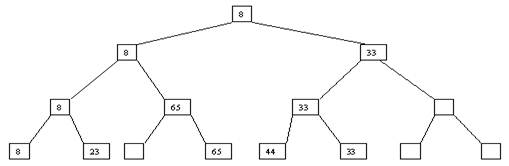
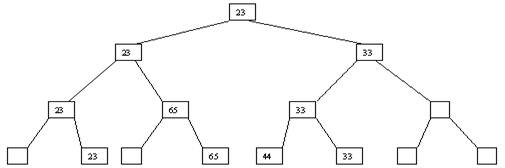
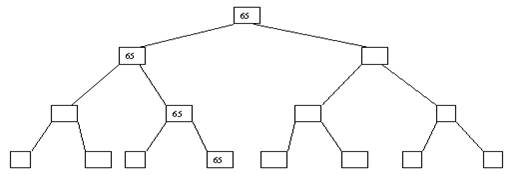
Рис. 2. Второй шаг Процесс продолжается до тех пор, пока все узлы дерева не будут заполнены фиктивными ключами (рисунки 3 - 8).
Принято называть " внешней" сортировкой сортировку последовательных файлов, располагающихся во внешней памяти и слишком больших, чтобы можно было целиком переместить их в основную память и применить один из методов внутренней сортировки. Методы внешней сортировки появились, когда наиболее распространенными устройствами внешней памяти были магнитные ленты. Сбалансированное N-ленточное слияние. Общей формой внешней сортировки является N -ленточное слияние. Для N -ленточного слияния потребуется 2N магнитных лент и 2N лентопротяжных устройств (которые можно заменить 2N файлами на устройстве внешней памяти). Исходная неупорядоченная последовательность размещается на первой магнитной ленте. Затем она разносится на N магнитных лент по следующему правилу: первая запись – на первую из N лент, вторая – на вторую, (N+1) -ая – снова на первую из N лент. Сбалансированное N -ленточное слияние осуществляется в два этапа. На первом этапе из записей, хранящихся на каждой магнитной ленте, формируются упорядоченные цепочки. Так как все цепочки имеют одинаковую длину, слияние называется сбалансированным. Упорядочение цепочки происходит в оперативной памяти одним из методов внутренней сортировки. Упорядоченные цепочки размещаются на N свободных магнитных лентах, после чего начинается второй этап сортировки – слияние. Процесс слияния осуществляется в несколько циклов. После каждого цикла слияния длина упорядоченных цепочек увеличивается на N. В конечном итоге, формируется упорядоченная последовательность из N составляющих. Собственно слияние осуществляется следующим образом. Пусть имеются две цепочки длиной l, изначально упорядоченные. Необходимо получить одну упорядоченную цепочку. Для этого: сравниваются первые элементы двух цепочек, меньшая переписывается в результирующую цепочку; операция осуществляется с помощью трех счетчиков; после записи в результирующую последовательность увеличивается на единицу счетчик результирующей последовательности и счетчик последовательности, в которой был обнаружен меньший элемент; действие повторяется до тех пор, пока один из счетчиков исходной последовательности не достигнет значения конца последовательности, после чего оставшиеся элементы другой последовательности дописываются в конец результирующей. Таким образом, будут упорядочены каждая из N магнитных лент.
Содержание отчета
|