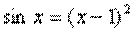Лабораторная работа № 6. Программирование элементарных численных методов
Цель работы: Приобретение навыков программирования элементарных численных методов. Краткие теоретические сведения Метод дихотомии (половинного деления). Правильное решение уравнения методом половинного деления возможно лишь в том случае, если известно, что на заданном интервале имеется корень, и он является единственным. Это совсем не означает, что метод дихотомии может использоваться только для решения линейных уравнений. Для нахождения корней уравнений более высокого порядка методом половинного деления необходимо сначала отделить корни по отрезкам. Алгоритм метода дихотомии очень прост. Рассмотрим отрезок |a, b|, в пределах которого имеется один корень x1 (рис. 11).
Рис. 11. Пример определения корня уравнения графическим способом На первом этапе вычисляется x0=(a+b)/2. Далее определяется значение функции в этой точке: если f(x0)< 0, то выбирают отрезок [a, x0], если наоборот, то [x0, b], т.е происходит сужение интервала. Таким образом, в результате формируется последовательность xi, где i - номер итерации. Вычисления прекращаются, когда разность b-a станет меньше требуемой погрешности. В качестве примера использования метода половинного деления найдем корень на интервале [0; 1] уравнения x3-3*x+1=0 с точностью в 10-3. Результаты расчета представлены в таблице 7. Таблица 7 Результаты расчета
Как видно из таблицы корнем является 0, 347. Количество итераций равно 10. Условие завершения: a – b = 0, 0009< 10-3 Метод половинного деления или метод дихотомии является наиболее простым для решения уравнения в численных методах. Метод Фибоначчи является одним из наиболее эффективных методов одномерной оптимизации выпуклых функций. Подобно методу золотого сечения, он требует двух вычислений функции на первой итерации, а на каждой последующей только по одному. Однако этот метод отличается от метода золотого сечения тем, что коэффициент сокращения интервала неопределенности меняется от итерации к итерации. Предварительный этап. Выбрать допустимую конечную длину интервала неопределенности l> 0 и константу различимости ζ > 0. Пусть задан начальный интервал неопределенности (b1 – a1). Выбрать общее число вычислений функции n так, чтобы Fn > (b1 – a1)/l. Положить λ 1 =a1 + Fn-λ (b1 – a1)/Fn, µ1 =a1 + Fn-l(b1 – a1)/Fn. Вычислить f(λ 1), f(µ1), положить k=1 и перейти к основному этапу. Основной этап. Первый шаг. Если f(λ k) > f(µk), то перейти ко второму шагу, в противном случае – к третьему шагу. Второй шаг. Положить ak+1 = λ k,, bk+1 = bk. Затем положить λ k+1 = µk,, µk+1 = ak+ 1 + Fn-k-1(bk+1 - ak+1)/Fn-k.. Если k = n-2, то перейти к пятому шагу, в противном случае вычислить f(µk+1) и перейти к четвертому шагу. Третий шаг. Положить ak+1 = ak, bk+1 = µk,, µk+1=λ k, λ k+1 = ak+1+ Fn-k-λ (bk+1 - ak+1)/Fn-k. Если k=n-2, то перейти к пятому шагу, в противном случае f(λ k+1) и перейти к четвертому шагу. Четвертый шаг. Заменить k на k+1 и перейти к первому шагу. Пятый шаг. Положить λ n = λ n-1, µn = λ n + ζ. Если f(λ n) > f(µn), то положить an = λ n, bn = bn-1. В противном случае (если f(λ n) < f(µn)), положить an = an-1, bn = µn. Конец: оптимальное решение содержится в интервале [ an, bn ]. Пример. Найти min f(x) = min(x2 + 2x) при условии -3≤ x≤ 5. Потребуем, чтобы длина конечного интервала неопределенности не превосходила 0, 2. Следовательно, Fn > 8/0.2 = 40, так что n=9. Выберем в качестве константы различимости значение ζ = 0.01. Два первых вычисления значений функции проводятся в точках λ 1 = 0.0545, µ1 = 1.945. Так как f(λ 1) < f(µ1), то новый интервал неопределенности будет равен [–3.000; 1.945]. Далее процедура повторяется аналогично. Результаты итераций приведены в табл.8. Конечный интервал неопределенности [a9, b9] равен [–1.109; –0.96 4], а его длина l = 0.145. За приближение положения точки минимума выберем середину интервала –1.0364. Таблица 8 Результаты расчета
Метод золотого сечения. Пусть на k -й итерации метода золотого сечения интервал неопределенности равен [ak, bk ]. Новый интервал неопределенности [ak+1, bk+1] будет равен [λ k, bk], если f(λ k) > f(µk) и [ak, µk] – в противном случае. Алгоритм золотого сечения. Предварительный этап. Выбрать допустимую конечную длину интервала неопределенности l > 0. Пусть [a1, b1] – начальный интервал неопределенности. Положить λ 1 = a1 + (1 – α)(b1 – a1), µ1= a1 + α (b1 – a1), где α = 0.618. Вычислить f(λ 1), f(µ1), положить k=1 и перейти к основному этапу. Основной этап. Первый шаг. Если bk – ak < l, то остановиться, оптимальная точка принадлежит интервалу [ak, bk ]. В противном случае, если f(λ k) > f(µk), то перейти ко второму шагу, а если f(λ k) ≤ f(µk), то к третьему шагу. Второй шаг. Положить ak+1 = λ k, bk+1 = bk, λ k+1 = µk, µk+1 = ak+1 + α (bk+1 - ak+1). Вычислить f(µk+1) и перейти к четвертому шагу. Третий шаг. Положить ak+1 = ak, bk+1 = µk, µk+1 = λ k, λ k+1 = ak+1 + (1-α)(bk+1 – ak+1). Вычислить Четвертый шаг. Заменить k на k+1 и перейти к первому шагу. Пример. Требуется найти min f(x) = min(x2 + 2x) при условии -3≤ x≤ 5. Очевидно, функция f(x) строго квазивыпукла и начальная длина интервала неопределенности равна 8. Сократим этот интервал неопределенности до интервала, длина которого не больше чем 0, 2. Определим первые две точки: λ 1 = -3 + 0.383 * 8 = 0.056 µ1 = -3 + 0.0619 * 8 = 1.944 Вычислив f(λ 1) и f(µ1), получим f(λ 1) < f(µ1). Следовательно, новый интервал неопределенности равен (-3; 1.941). Находим µ2 = λ 1 = 0.056 λ 2 = a2 + (1 – λ)(b2 – a2) = -3 + 0.382 * 4.944 = -1.112 На этом первая итерация заканчивается. Далее процесс поиска продолжается аналогично. Результаты вычислений приведены в табл.9. После восьми итераций, содержащих девять вычислений функции, интервал неопределенности оказывается равным (-1.112; -0.936), так что в качестве точки минимума может быть взята, например, середина этого интервала –1.024. Заметим, что точкой точного минимума является точка –1.0. Таблица 9 Результаты расчета
Метод квадратичной интерполяции. Этот метод основан на замене f(x) в промежутке x0 ±h квадратичной параболой, экстремум которой вычисляется аналитически. После приближенного нахождения экстремума x* (максимума или минимума) можно задать x0 = x* и повторить поиск. Таким образом, с помощью итерационной процедуры значение x* уточняется до получения его с заданной точностью ε. Алгоритм метода следующий: Задаем начальное приближение x0 для x* и вычисляем два смежных значения аргумента f(x) x1 = x0 - h и x2 = x0 + h, где h -полуинтервал поиска. Вычисляем три значения f(x0), f(x1), f(x2). Находим коэффициенты параболы a, b, c (считая, что f(x) на указанном отрезке представляет собой параболу ax2 + bx + c) и по найденным коэффициентам вычисляем положение экстремума x * = -b / 2a. Проверяем условие |x*-x0|< ε. Если условие не выполняется, задаем x0=x* и идем к пункту 1. Если выполняется, считаем x* найденным с заданной точностью ε, идем к пункту 5. Выводим на печать x* и f(x*).
Содержание отчета
1. Титульный лист 2. Задание + вариант 3. Блок-схема или пошаговое описание алгоритма 4. Текст программы 5. Пример выполнения: выходной файл
Задание
Написать программу, осуществляющую поиск оптимального значения функции или решение уравнения заданным методом. Интервал поиска (или начальную точку – в зависимости от метода) вводит пользователь. На экране пользователю должен отображаться ход решения, т.е. все промежуточные точки и значения функции в этих точках. Начальные условия (функция, интервал/начальная точка) и ход поиска должны дублироваться в текстовый файл. Имя файла вводит пользователь.
Варианты алгоритмов оптимизации: метод дихотомии, метод Фибоначчи, метод золотого сечения, метод квадратичной интерполяции. Функция: Интервал/начальную точку выбирать в пределах [-10; 10]. Произвести отделение корней уравнений на интервале [0.1, 5.0], уточнить их значения до ε = 5· 10-6 методами половинного деления, простой итерации, касательных и секущих. Сравнить полученные результаты. 1. 2. 3. 4. 5. 6. 7. 8. 9.
Пример выполнения работы
Алгоритм оптимизации: метод секущих, касательных. Функция: Блок – схема программы представлена на рис. 11.
Метод секущих Метод касательных
Рис. 11. Блок-схема программы Листинг программы #include < stdio.h> #include < stdlib.h> #include < conio.h> #include < math.h> float f (float x) { return sin(x*x/10)*exp(x/10)/(x*x+1); } float d1 (float x) { return (exp(x/10)*((x*x-20*x+1)*sin(x*x/10)+2*(x*x*x+x)*cos(x*x/10)))/(10*(x*x+1)*(x*x+1)); } float d2 (float x) { return (exp(x/10)*(4* (pow(x, 5)-15 *pow(x, 4)+2*pow(x, 3)-10* x*x+x+5) *cos(x*x/10)-(4*pow(x, 6)+7*pow(x, 4)+40 *pow(x, 3)-598*x*x+40* x+199)* sin(x*x/10)))/(100*pow((x*x+1), 3)); }
void kos (void) // метод касательных { FILE* fp=fopen(" result.txt", " w"); fprintf (fp, " y=sin(x*x/10)*exp(x/10)/(x*x+1)\n"); float a, b, x0, x1, eps, temp; printf (" Vvedite otrezok, prinadlezhashego intervalu (-10; 10): "); scanf (" %f%f", & a, & b); printf (" Vvedite okrestnost: "); scanf (" %f", & eps); fprintf (fp, " Otrezok: [%f, %f], eps=%f\n", a, b, eps); if (f(a)*d2(a)> 0) { x0=a; x1=b; } else { x0=b; x1=a; } while (fabs(x0-x1)> eps) { temp=x0; x0=temp-f(temp)/d1(temp); x1=temp; printf (" x=%f\t", x0); fprintf (fp, " x=%f\t", x0); printf (" y=%f\n", f(x0)); fprintf (fp, " y=%f\n", f(x0)); } printf (" x*=%f", x0); fprintf (fp, " x*=%f", x0); printf (" \ty=%f", f(x0)); fprintf (fp, " \ty=%f", f(x0)); fclose (fp); getch(); }
void main (void) //метод секущих { FILE* fp=fopen(" result.txt", " w"); fprintf (fp, " y=sin(x*x/10)*exp(x/10)/(x*x+1)\n"); float constant, temp, a, b, x, eps; printf (" Vvedite conci otrezka, prinadlezhashego intervalu (-10; 10): "); scanf (" %f%f", & a, & b); printf (" Vvedite okrestnost: "); scanf (" %f", & eps); fprintf (fp, " Otrezok: [%f, %f], eps=%f\n", a, b, eps); if (d1(a)*d2(a)> 0) { x=a; constant=b; do { temp=f(x)*(constant-x)/(f(constant)-f(x)); x=x-temp; printf (" x=%f\t", x); fprintf (fp, " x=%f\t", x); printf(" y=%f\n", f(x)); fprintf(fp, " y=%f\n", f(x)); } while (fabs(temp)> eps); } else { x=b; constant=a; do { temp=f(x)*(x-constant)/(f(x)-f(constant)); x=x-temp; printf (" x=%f\t", x); fprintf (fp, " x=%f\t", x); printf(" y=%f\n", f(x)); fprintf(fp, " y=%f\n", f(x)); } while (fabs(temp)> eps); } printf (" x*=%f\t", x); fprintf (fp, " x*=%f\t", x); printf (" y=%f\n", f(x)); fprintf(fp, " y=%f", f(x)); fclose(fp); getch(); kos(); }
ЛИТЕРАТУРА 1. Ахо, А. В. Структуры данных и алгоритмы / А. В. Ахо, Дж. Хопкрофт, Дж. Д. Ульман. – М.: " Вильямс", 2000. – 384 с. 2. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях. – М.: Высшая школа, 2000. – 190 с. 3. Борисов В.М. Разработка пакетов программ вычислительного типа. –М.: Издательство МГУ, 1990. – 123 с. 4. Вендеров А.М. Проектирование программного обеспечения экономических информационных систем. – М.: Финансы и статистика, 2002.- 348 с. 5. Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения). – М.: Высшая школа, 2001.-384 с. 6. Гмурман В.Е. Теория вероятностей и математическая статистика. –М.: Высшая школа, 2000.- 480 с. 7. Единая система программной документации.- М.: Изд-во стандартов, 1994. - 128 с. 8. ЕСПД. Схемы алгоритмов. Программ, данных и систем. ГОСТ 7.1-84. Москва, Государственный комитет по управлению качеством продукции и стандартам, 1990.-26 с. 9. Кнут, Д. Э. Искусство программирования, том 3. Сортировка и поиск / Д. Э. Кнут. – М.: " Вильямс", 2000. – 832 с. 10. Кондратьева, С. Д. Введение в структуры данных / С. Д. Кондратьева. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 376 с. 11. Макконнелл, Дж. Основы современных алгоритмов / Дж. Макконнелл. – М.: Техносфера, 2004. – 368 с. 12. Орлов С.А. Технология разработки программного обеспечения. Питер, 2002. – 464 с.
Содержание
УЧЕБНОЕ пособие ТЕХНОЛОГИИ ПРОГРАММИРОВАНИЯ. ЛАБОРАТОРНЫЙ ПРАКТИКУМ для студентов направления 230100 – Информатика и вычислительная техника (Вычислительные машины, комплексы, системы и сети)
Лаврухина Тамара Владимировна
Редактор Остроухова Г.Н. Подписано в печать 03.11.12 Формат 60x84 1/16. Бумага офсетная Ризография. Печ.л. _____ Тираж экз. 100
Липецкий филиал Международного института компьютерных технологий 398600, Липецк, проезд Кувшинова, 5Б. Типография ЛФ МИКТ, 398600, Липецк, проезд Кувшинова, 5Б.
|

 и перейти к четвертому шагу.
и перейти к четвертому шагу. .
.