Но равенство нулю коэффициента корреляции означает отсутствие только линейной связи. Если Кф<0,то связь между признаками обратная. Если Кф>0, то связь - прямая
Коэффициент линейной парной корреляции, rx, y - используется для оценки степени тесноты линейной связи. Строится как отношение показателя ковариации к произведению среднеквадратических отклонений признаков X и Y:
Ковариация, cov (X, Y) – это показатель совместной вариации признаков; вычисляется он следующим образом:
Это размерный показатель; его единицы измерения равны произведению единиц измерения Х на единицы измерения Y. Свойства ковариации: 1. cov (X, X) = sх2; 2. cov (X, A) =0, где A -const; 3. cov (X, Y+Z) = cov (X, Y) + cov (X, Z), где X, Y, Z – случайные величины. Линейный коэффициент корреляции в отличие от ковариации – показатель безразмерный и поэтому легко интерпретируемый. Он может быть рассчитан также по формуле:
где
sх, sy – средние квадратические отклонения признака-фактора и признака-результата. Область допустимых значений линейного коэффициента корреляции от -1 до +1. Если значение коэффициента корреляции по модулю близко к единице, то связь близка к линейной функциональной. Если признаки Х и Y взаимно независимы, то значение коэффициента корреляции близко к нулю. Равенство нулю коэффициента корреляции означает отсутствие только линейной связи. Признаки же могут быть связаны тесной нелинейной связью и при этом иметь нулевой коэффициент корреляции (например, в случае параболической формы связи). Отрицательные значения коэффициента корреляции свидетельствуют об обратной зависимости признаков, положительные значения свидетельствуют о прямой зависимости. Линейный коэффициент парной корреляции может быть рассчитан по сгруппированным данным, а именно, по данным комбинационной группировки.
В этом случае формула расчета линейного парного коэффициента корреляции следующая:
где N – объем совокупности; Nij, Nxi, Nyj – частоты распределения значений признаков. Если сравнить значения эмпирического корреляционного отношения r с абсолютным значением линейного парного коэффициента корреляции │ r │, то можно сделать вывод о форме связи. Если r -| r |> 0, 1, то связь скорее нелинейная, если данное неравенство не выполняется, то связь скорее линейная. Рассчитаем коэффициент Фехнера и линейный парный коэффициент корреляции между признаками Расходы на рекламу (X) и Объем продаж (Y) по данным наблюдений 15 предприятий. Исходные данные представлены в табл. 4.1. Расчеты представлены в табл. 4.4. Кф =(13-2)/(13+2)=0, 735. Так как значение Кф стремится к единице, то связь тесная, а положительное значение Кф свидетельствует о прямой зависимости. Рассчитаем коэффициент линейной парной корреляции:
Вывод: зависимость между признаками Расходы на рекламу и Объем продаж можно характеризовать как довольно тесную (r → 1) и возрастающую (т.к. r > 0). Сравним значения эмпирического корреляционного отношения r и линейного парного коэффициента корреляции | r |. Значение эмпирического корреляционного отношения для наших данных составило: r =0, 87 (см. пример выше). Так как r - | r | =0, 87 – 0, 94 = - 0, 07 < 0, 1, то связь между признаками расходы на рекламу и объем продаж скорее линейная, чем нелинейная. Таблица 4.4 Расчет коэффициента Фехнера
Регрессионный анализ. Метод наименьших квадратов. Линейная однофакторная регрессия Регрессия – зависимость среднего значения какой-либо случайной величины от одной или нескольких независимых величин. Термин «регрессия» (спад) впервые ввели шведские статистики (Френсис Гамильтон) в работе, в которой исследовалась зависимость х (отклонения роста отца от среднего уровня) от y (отклонение роста взрослого сына от среднего уровня). Оказалось, что эта зависимость обратная. Т.е. наблюдалась тенденция к регрессии: у очень высоких отцов дети в среднем ниже ростом, а у очень низкорослых отцов дети в среднем значительно выше своих родителей. Уравнение регрессии – уравнение связи в среднем (описываемое графически аналитической линией регрессии) – это уравнение, описывающее корреляционную зависимость между признаком-результатом y и признаками факторами (одним или несколькими). Наиболее часто для описания статистической связи признаков используется линейное уравнение регрессии. Внимание к линейной форме связи объясняется четкой экономической интерпретацией параметров линейного уравнения регрессии, ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. Методы выявления формы связи: - графический (вид корреляционного поля и эмпирической линии регрессии); - опыт предыдущих аналогичных исследований; - перебор всевозможных видов функций и выбор наилучшей по показателю качества. Линейное парное (однофакторное) уравнение регрессии имеет вид: M (y │ x = xi)= b 0+ b 1· x i, где M (y │ x = xi) – условное мат. ожидание зависимой переменной y при значении независимой переменной х равном хi; b 0, b 1 – параметры (коэффициенты) уравнения регрессии. При построении уравнения регрессии y = f (x) мы должны определить вид уравнения (вид функциональной связи) и оценить параметры регрессии по имеющимся данным наблюдений y, x. Оценки параметров линейной регрессии (b 0 и b 1) могут быть найдены разными методами: методом наименьших квадратов; методом максимального правдоподобия; примитивными методами. Требование к методам оценивания: они должны быть по возможности просты, давать состоятельные, эффективные и несмещенные оценки. Наиболее распространенным методом оценки параметров является метод наименьших квадратов (МНК), который при определенных условиях дает состоятельные эффективные и несмещенные оценки. Данный метод используют для оценивания не только параметров регрессии, но и других статистических характеристик (параметров), например, среднего значения. Суть МНК: Пусть имеются n наблюдений признаков х и y. Причем известен вид уравнения регрессии: f (x, bj) (известен вид функции - f), bj - параметры функции. Задача состоит в оценке параметров (т.е. определении значений оценок –
Проиллюстрируем суть данного метода графически (рис. 4.4.). Попытаемся подобрать прямую линию, которая ближе всего расположена к точкам корреляционного поля. Согласно методу наименьших квадратов прямая подбирается так, чтобы сумма квадратов расстояний по вертикали между точками корреляционного поля и этой линией была бы минимальной.
x i Рис. 4.4. Линия регрессии с минимальной суммой квадратов отклонений.
Значения yi и xi i =1; n нам известны, это данные наблюдений. В функции S они представляют собой константы. Переменными в данной функции являются искомые оценки параметров – В результате получим систему из двух нормальных линейных уравнений:
Решая данную систему, найдем искомые оценки параметров:
Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм Оценка параметра b 1 может быть рассчитана также через коэффициент корреляции: Формально значение параметра b 0 – среднее значение признака-результата y при значении признака-фактора х равном нулю. Если признак-фактор не имеет и не может иметь нулевого значения, то вышеуказанная трактовка параметра b 0 не имеет смысла. Данный параметр имеет также смысл среднего значения результата, сформировавшегося под влиянием неучтенных в модели факторов. МНК-оценки параметров являются «наилучшими» (состоятельными, несмещенными и эффективными) оценками параметров уравнения регрессии. Построим аналитическое уравнение регрессии, описывающее зависимость объема продаж, (y) от расходов на рекламу (х) по данным о 15 предприятиях: f (xi) = b 0+ b 1· xi.
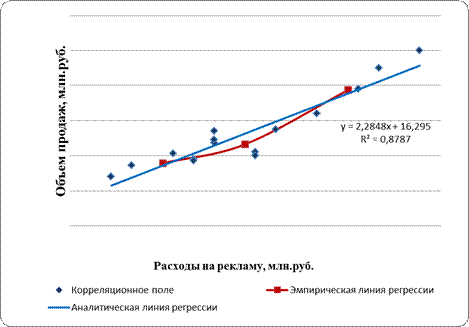
Окончательно аналитическое уравнение регрессии примет вид: f (xi)= 16, 30+2, 29· хi Параметр b1 = 2, 29 показывает, что при увеличении расходов на рекламу на 1 млн. руб. объем продаж возрастает в среднем на 2, 29 млн. руб. Параметр b0 = 16, 3 можно проинтерпретировать следующим образом – при отсутствии расходов на рекламу объем продаж предприятия составит 16, 3 млн. руб., однако такая интерпретация не вполне корректна, поскольку среди исходных данных нет предприятий с расходами на рекламу равными или близкими к нулю. Графическое отображение полученного уравнения регрессии представлено на рис. 4.5. После построения уравнения регрессии следует оценить его качество. Оценка качества уравнения осуществляется в два этапа: 1) Оценивается адекватность уравнения регрессии данным наблюдений (т.е. степень близости рассчитанных по данному уравнению значений признака-результата f (x) к фактическим значениям y). 2) Оценивается надежность уравнения регрессии (то есть возможность использовать данное уравнение для данных наблюдений другой выборки).
Рис. 4.5. Корреляционное поле, эмпирическая и аналитическая линии регрессии Для оценки адекватности качества полученного уравнения регрессии используется ряд показателей. Наиболее широкое применение из них получил теоретический коэффициент детерминации, R2yx. Теоретический коэффициент детерминации рассчитывается, как отношение объясненной уравнением дисперсии признака-результата - d2, к общей дисперсии признака-результата s2y:
где d2 – объясненная уравнением регрессии дисперсия y, s2y - общая (полная) дисперсия y. В силу теоремы о сложении дисперсий общая дисперсия результативного признака равна сумме объясненной уравнением регрессии d2 и остаточной (необъясненной) e2 дисперсий: s2y=d2+e2. Поэтому коэффициент детерминации может быть рассчитан через остаточную и общую дисперсии:
где e2 - остаточная дисперсия y, Данный показатель характеризует долю вариации (дисперсии) результативного признака y, объясняемую уравнением связи (а, следовательно, и фактором х), в общей вариации (дисперсии) y. Коэффициент детерминации R 2 yx принимает значения от 0 до 1. Соответственно величина 1- R 2 yx характеризует долю дисперсии y, вызванную влиянием прочих неучтенных в уравнении факторов и ошибками измерений. При парной линейной регрессии R 2 yx = r 2 yx. Средняя квадратическая ошибка уравнения регрессии, se - представляет собой среднее квадратическое отклонение наблюдаемых значений результативного признака от теоретических значений, рассчитанных по модели, т.е.:
где h – число параметров в модели регрессии. В случае линейной парной регрессии h = 2 (b 0, b 1). Величину средней квадртической ошибки можно сравнить со средним квадратическим отклонением результативного признака sy. Если se окажется меньше sy, то использование модели регрессии является целесообразным. Средняя ошибка аппроксимации, А:
Чем меньше рассеяние эмпирических точек вокруг теоретической линии регрессии, тем меньше средняя ошибка аппроксимации. Ошибка аппроксимации меньше 7% свидетельствует о хорошем качестве модели. Выбор вида уравнения регрессии (вида функции) обычно осуществляется методом сравнения величины показателя адекватности, рассчитанного при разных видах зависимости. Если показатели адекватности оказываются примерно одинаковыми для нескольких функций, то предпочтение отдается более простым видам функций, ибо они в большей степени поддаются интерпретации и требуют меньшего объема наблюдений. Оценим качество уравнения регрессии для данных предыдущего примера: R2yx = r2yx = 0, 942 = 0, 88. Это означает, что 88% вариации объема продаж предприятия объясняется уравнением регрессии f (xi)= 16, 30+2, 29· xi. То есть уравнение достаточно качественное. При оценки надежности уравнения регрессии используют статистические методы проверки гипотез. Предполагается, что данные наших наблюдений неполные, т.е. выборочные. При переходе от одной выборки наблюдений к другой значения оценок параметров и признака-результата будут меняться. Насколько сильна вариация этих оценок? Если вариация умеренная, то уравнение регрессии, полученное по данным конкретных наблюдений, можно использовать и для генеральной совокупности, т.е. уравнение надежно. Для проверки гипотезы о надежности уравнения регрессии используют статистику, рассчитываемую по следующей формуле:
где n - число наблюдений; h – число оцениваемых параметров (в случае парной линейной регрессии h =2); R2y(x1,..., xm) - выборочный коэффициент детерминации. Данная статистика имеет F -распределение (Фишера-Снедоккора). Поэтому для поиска критического значения - Fкр пользуются таблицами распределения Фишера-Снедоккора, задаваясь при этом уровнем значимости a (обычно его берут равным 0, 05) и двумя числами степеней свободы k 1= h -1 и k 2= n-h. Сравнивая фактическое значение F -статистики критерия, вычисленное по данным наблюдений - (F набл) с критическим - F кр(a; k 1; k 2). Если F набл< F кр(a; k 1; k 2), то основную гипотезу о незначимости уравнения регрессии не отвергают. Если F набл> F кр(a; k 1; k2), то основную гипотезу отвергают и принимают альтернативную гипотезу о статистической значимости уравнения регрессии. Для уверенных выводов отличие наблюдаемого и критического значений F -критерия должно быть по крайней мере в 4 раза. Оценим надежность уравнения регрессии для примера, рассмотренного выше. Для этого рассчитаем наблюдаемое значение F -статистики:
По таблицам Фишера найдем критическое значение: Fкр(0, 05; 1; 10) = 4, 96. Так как Fнабл> Fкр, то уравнение f(xi) = 16, 30+2, 29·xi можно признать значимым и надежным с вероятностью 0, 95. Некоторые нелинейные функции регрессии Несмотря на распространенность линейных функций регрессии, встречаются случаи, когда с помощью линейной функции невозможно описать связи между конкретными явлениями. Такая ситуация может быть проиллюстрирована корреляционным полем, отражающим явный нелинейный характер зависимости (рис. 4.6). В отдельных случаях требуется специально выявить свойства взаимосвязи, не отражаемые линейным уравнением (например, выпуклость). Корреляционное поле на рис. 4.6. свидетельствует о существенно нелинейном характере связи. По мере приближения значений x к нулю значения y возрастают очень сильно. В таких случаях могут быть использованы функции регрессии, обращающиеся в бесконечность при x = 0. Простейшая функция такого рода описывает гиперболу вида:
Рис. 4.6. Корреляционное поле, иллюстрирующее нелинейную зависимость Применим к данному случаю системы нормальных уравнений, справедливую для любых функций регрессии. Поскольку в нашем случае
Решая данную систему уравнений, получаем оценки параметров уравнений регрессии. Аналогично преобразовывается система нормальных уравнений для степенной, логарифмической, экспоненциальной и других функций. Если исследуемая зависимость характеризуется непропорциональным ростом результирующего признака y по мере увеличения признака-фактора x, то выпуклость функции может быть выявлена при описании зависимости трехчленом второй степени:
Функция регрессии содержит три параметра, следовательно, требуется составить систему из трех нормальных уравнений. Таким образом, система принимает вид:
Более сложные зависимости могут быть отражены полиномами более высоких степеней. Требуется описать представленную зависимость (табл. 4.5) с помощью нелинейной функции регрессии. Таблица 4.5 Исходные и расчетные данные для нахождения параметров нелинейной (гиперболической) регрессии
Для описания данной зависимости лучше всего подходит гипербола. Построим систему нормальных уравнений для получения параметров уравнения регрессии:
Решая данную систему уравнений, получаем параметры уравнения регрессии, которое принимает вид:
Проиллюстрируем полученное аналитическое описание зависимости на графике (рис. 4.7.).
Рис. 4.7. Корреляционное поле и гиперболическая функция регрессии. Линейная множественная регрессия. Коэффициент множественной корреляции. Многомерный статистический анализ Рассмотрим теперь случай, когда на результирующий признак оказывают влияние не один, а несколько признаков-факторов. Сложность такой задачи определяется тем, что различные факторы действуют на признак-результат не изолированно, и зависимость от набора факторов не равна простой сумме зависимостей от каждого фактора в отдельности. Взаимосвязь между результирующим признаком и признаками-факторами приходится исследовать на фоне взаимосвязи между признаками-факторами. Структуру таких связей можно представить схематически (рис. 4.8.). В общем виде уравнение, описывающее множественную связь можно представить следующим образом:
где Y – признак-результат; X 1, X 2,..., Xm – признаки-факторы; u – случайная составляющая.
Рис. 4.8. Граф связей модели двухфакторной регрессии. Таким образом, многомерный статистический анализ сводится к следующим этапам: 1. сравнение степени влияния различных факторов на признак-результат; 2. выделение прямого (непосредственного) влияния фактора на признак-результат и косвенного (опосредованного) влияния фактора на результат (через другие факторы); 3. выявление существенности влияния данного фактора (или группы факторов) на результат на фоне других факторов (иначе говоря, необходимо выяснить, нельзя ли исключить из модели данный фактор без существенного ухудшения описания результирующей переменной); 4. построение модели множественной регрессии. Уравнение регрессии в стандартном масштабе связывает стандартизованные значения признаков. То есть все значения исследуемых признаков переводятся в стандарты по формулам: - для признаков – факторов
где Хji - значение переменной Хji в i -ом наблюдении; - для признака – результата
Таким образом, начало отсчета каждой стандартизованной переменной совмещается с ее средним значением, а в качестве единицы изменения принимается ее среднее квдратическое отклонение. Благодаря этому все переменные в стандартизованном масштабе имеют одинаковые средние арифметические значения равные 0 ( Если связь между переменными в естественном масштабе линейная, то изменение начала отсчета и единицы измерения этого свойства не нарушат, так что и стандартизованные переменные будут связаны линейным соотношением:
где b j – параметры уравнения регрессии в стандартном масштабе. b - коэффциенты могут быть оценены с помощью обычного МНК. При этом система нормальных уравнений будет иметь вид: rx1y = b 1+ rx1x2b 2 +…+ rx1xmbm rx2y= rx2x1b 1+ b 2+…+ rx2xmbm … rxmy= rxmx1b 1+ rxmx2b 2+…+ bm Найденные из данной системы b – коэффициенты показывают на какую часть своего среднего квадратического отклонения изменится признак-результат Y с изменением соответствующего фактора Хj на величину своего среднего квадратического отклонения (sхj) при неизменном влиянии прочих факторов (входящих в уравнение). Кроме того, коэффициент bj может интерпретироваться как показатель прямого (непосредственного) влияния j -ого фактора (Xj) на результат (Y). Во множественной регрессии j -ый фактор оказывает не только прямое, но и косвенное (опосредованное) влияние на результат (т.е. влияние через другие факторы модели). Косвенное влияние измеряется величиной:
где m – число факторов в модели. Полное влияние j -ого фактора на результат, равное сумме прямого и косвенного влияний, измеряет коэффициент линейной парной корреляции данного фактора и результата – rxj, y. Таким образом:
Отбор факторов в уравнение множественной регрессии обычно осуществляется в два этапа: 1. теоретический (содержательный) анализ взаимосвязи результата и факторов, оказывающих на него существенное влияние; 2. количественная оценка (расчет соответствующих показателей) и анализ взаимосвязи факторов с результатом. При линейной форме связи между признаками данный этап сводится анализу корреляционной матрицы (матрицы парных линейных коэффициентов корреляции). Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: - Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов). - Каждый фактор должен быть достаточно тесно связан с результатом (при линейной связи коэффициент парной корреляции фактора с результатом rxj, y должен существенно отличаться от нуля). - Факторы не должны быть коррелированы друг с другом, тем более находиться в строгой функциональной связи (т.е. они не должны быть интеркоррелированы). Разновидностью интеркоррелированности факторов является мультиколлинеарность – наличие высокой линейной связи между всеми или несколькими факторами. Мультиколлинеарность может привести к нежелательным последствиям: 1. затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; 2. становится невозможным определить изолированное влияние факторов на результативный показатель. Корреляционная матрица – это квадратная матрица размером (m +1; m +1) m – число факторов в модели. Ее размер определяется числом признаков, участвующих в анализе: m признаков-факторов и один признак-результат. Анализ корреляционной матрицы позволяет: - ранжировать факторы по степени их влияния на результат; - выявить мультиколлинеарные факторы. Таким образом, анализ корреляционной матрицы позволяет решить вопрос о составе факторов в уравнении множественной регрессии. Параметры уравнения линейной множественной регрессии оцениваются из системы нормальных уравнений, которая в общем случае имеет вид:
Решая данную систему уравнений, параметры bj могут быть определены, например, методом Гаусса. Другим методом оценки параметров bj служит нахождение их через параметры уравнения регрессии в стандартных масштабах, то есть b - коэффициенты:
Коэффициент регрессии bj при факторе Хj в уравнении называют условно-чистым коэффициентом регрессии. Он измеряет среднее по совокупности отклонение признака-результата от его средней величины при отклонении признака-фактора Хj на единицу, при условии, что все прочие факторы модели не изменяются (зафиксированы на своих среднихуровнях). Если не делать предположения о значениях прочих факторов, входящих в модель, то это означает, что каждый из них при изменении Хj может также изменяться (т.к. факторы (пусть и несильно) связаны между собой). Изменение прочих факторов модели вызовет изменение признака-результата. Таким образом, изменение признака-результата будет обусловлено изменением всех факторов модели, а не только интересующего нас фактора Хj. Коэффициенты множественной детерминации и корреляциихарактеризуют совместное влияние всех факторов на результат. Кроме того, они используются как показатели качества уравнения множественной регрессии. Коэффициент множественной детерминации, R2y(x1,..., xm ) – это теоретический коэффициент детерминации для случая множественной регрессии. По аналогии с парной линейной регрессией он определяется, как отношение дисперсии признака-результата, объясненной уравнением множественной регрессии – d 2, к общей дисперсии признака-результата – s2 y. Область допустимых значений R2y(x1,..., xm) от нуля до единицы. Данный показатель характеризует долю вариации признака-результата, объясненную уравнением регрессии (а, следовательно, и факторами включенными в данное уравнение), в общей вариации признака-результата. Для линейного уравнения регрессии данный показатель может быть рассчитан через b - коэффициенты, как:
Коэффициент множественной корреляции, Ry(x1,..., xm) - рассчитывается как корень из коэффициента множественной детерминации:
Данный показатель аналогичен линейному парному коэффициенту корреляции - rx, y, используемому в парном регрессионном анализе. Но в отличие от него Ry(x1,..., xm) может принимать значения только от нуля до единицы, следовательно, не может служить характеристикой направления связи. Чем плотнее фактические значения Yi располагаются относительно линии регрессии, тем меньше остаточная дисперсия и, следовательно, больше величина Ry(x1,..., xm ). Таким образом, при значении Ry(x1,..., xm ) близкомк единице уравнение регрессии лучше описывает фактические данные, и факторы сильнее влияют на результат; при значении Ry(x1,..., xm ) близком к 0 уравнение регрессии плохо описывает фактические данные и факторы оказывают слабое воздействие на результат.
Контрольные вопросы 1. Какие виды связей принято выделять в статистике? 2. Опишите порядок изучения парной статистической связи. 3. В чем состоит суть дисперсионного анализа? 4. Какие показатели используют для измерения тесноты связи в статистике?
|

 .
. .
. ,
,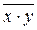 – среднее из произведения значений признака-фактора и признака-результата;
– среднее из произведения значений признака-фактора и признака-результата;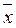 ,
,  - средние значения признака-фактора и признака-результата;
- средние значения признака-фактора и признака-результата;




 ), которые подбираются таким образом, чтобы минимизировать сумму квадратов отклонений фактических значений результативного признака – yi от расчетных (теоретических) значений – f (xi) (рассчитанных по уравнению регрессии):
), которые подбираются таким образом, чтобы минимизировать сумму квадратов отклонений фактических значений результативного признака – yi от расчетных (теоретических) значений – f (xi) (рассчитанных по уравнению регрессии): .
.
 y
y





 f(xi)
f(xi) X
X и
и  . Чтобы найти минимум функции двух переменных необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их нулю, т.е.
. Чтобы найти минимум функции двух переменных необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их нулю, т.е.  .
.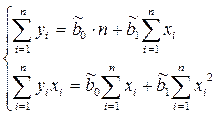

 (возможно некоторое расхождение из-за округления расчетов).
(возможно некоторое расхождение из-за округления расчетов). . Знак коэффициента регрессии b 1 указывает направление связи (если b 1> 0, связь прямая, если b 1< 0, то связь обратная). Величина b 1 показывает на сколько единиц изменится в среднем признак-результат – y при изменении признака-фактора – х на 1 единицу своего измерения.
. Знак коэффициента регрессии b 1 указывает направление связи (если b 1> 0, связь прямая, если b 1< 0, то связь обратная). Величина b 1 показывает на сколько единиц изменится в среднем признак-результат – y при изменении признака-фактора – х на 1 единицу своего измерения. ;
; .
.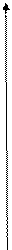

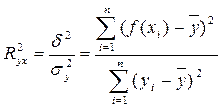 ,
,
 ,
,


 ,
,




 , то система нормальных уравнений принимает вид:
, то система нормальных уравнений принимает вид:



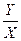








 ,
,  ,
, .
. ) и одинаковые дисперсии равные 1 (stx 2 =sty 2=1). Кроме того, коэффициент парной линейной корреляции между стандартизованными переменными равен среднему из произведений данных стандартизованных переменных:
) и одинаковые дисперсии равные 1 (stx 2 =sty 2=1). Кроме того, коэффициент парной линейной корреляции между стандартизованными переменными равен среднему из произведений данных стандартизованных переменных:  ,
,  .
. ,
,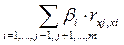 ,
, .
.
 , j=1; m;
, j=1; m;  .
. .
. .
.


