Расчет координат вспомогательного графика
Начнем расчеты сбросных расходов по интервалам. I интервал. Приток за первый интервал Qср× Dt=0, 36 (графа 4, табл. 11). На начало 1-го интервала (см. графы 5, 6, 7 табл. 11) q1=0; q1Dt =0 и
Записываем это значение в графу 7 табл.11 на конец 1-го интервала, по вспомогательному графику (рис.16, б) при 2 интервал. Qср Dt =2, 95. По уравнению Гильденблата
По вспомогательному графику этому значению соответствует q2=10 м3/с. Записываем последние два значения в графы 7 и 5 табл.111 на конец 2-го интервала. Подсчитываем qDt=1, 73 и ведем расчет дальше.
Рис. 16. Расчет пропуска расчетного паводка через глухой водослив с отметкой порог на НПУ: а - гидрограф паводка и кривая сбросных расходов; б - вспомогательный график метода Гильденблата. 3 интервал. QсрDt=6, 65 млн.м3; q1=10, 0; q1Dt=1, 73;
Вычисляем значение бинома на конец 3-го интервала: На рис. 16, а следует вынести в конце каждого интервала точки с ординатами, равными значениями q из графы 5 табл.11, и через эти точки провести кривую сбросных расходов, которая представляет собой не что иное, как гидрограф паводка в нижнем бьефе. Производить расчет в табл.11 имеет смысл лишь до максимального значения qm=230 м3/c, так как наша цель как раз состоит в определении этой величины, и затем по уравнению (20) находим
Коэффициент регулирования максимального расхода
Итак, мы определили максимальный напор на водосливе, иначе говоря, нашли максимальное превышение уровня ФПУ над НПУ при пропуске паводка через водослив шириной 60, 0 м с коэффициентом m=0, 46. Отметка этого максимального уровня ФПУ=15, 0+1, 53=16, 53 м. При этом V=54 млн.м3 и площадь зеркала при ФПУ=14, 6 км2. Удельный расход сброса В данном конкретном примере это объясняется тем, что регулирующий объем Vрег=28 млн.м3 практически несоизмерим с объемом паводка, который приближенно равен площади треугольника (рис.16, а):
Если заранее известно, что объем паводка во много раз больше объема регулирующей призмы, то нет смысла вести расчет кривой сбросных расходов и можно принять qmP = QmP.
|

 = 0. Подставляем эти значения в правую часть уравнения Гильденблата:
= 0. Подставляем эти значения в правую часть уравнения Гильденблата: = 0, 36+0-0=0, 36.
= 0, 36+0-0=0, 36. =0, 36 являются начальными для второго интервала.
=0, 36 являются начальными для второго интервала.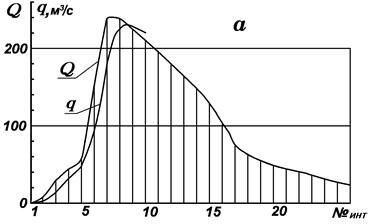

 м
м
 м3/с на 1 пог.м, что находится в пределах допустимого (5-6 м3/с на 1 пог.м при q< 100 м3/с и 10-16 м3/с 1 пог.м при q< 400 м3/с). Кривая сбросных расходов q(t) (рис. 16, а) почти полностью повторяет очертания гидрографа Q(t) с небольшим сдвигом во времени. Максимальный расход сброса почти равен максимуму притока (230 и 235 м3/с).
м3/с на 1 пог.м, что находится в пределах допустимого (5-6 м3/с на 1 пог.м при q< 100 м3/с и 10-16 м3/с 1 пог.м при q< 400 м3/с). Кривая сбросных расходов q(t) (рис. 16, а) почти полностью повторяет очертания гидрографа Q(t) с небольшим сдвигом во времени. Максимальный расход сброса почти равен максимуму притока (230 и 235 м3/с). млн.м3.
млн.м3.


