Расчет ординат ССК стока воды в р. Ашлык у с. Ашлык
Если расходом сокращения является средняя арифметическая величина (для расчетного года – средний годовой расход, для длительной группы лет – средний из средних годовых, то есть норма стока), то ССК выходит из начала координат, а ее последняя ордината равна нулю:
В табл. 13 показано преобразование хронологического ряда средних годовых расходов воды в р.Ашлык в аналогичный ряд модульных коэффициентов, а затем в сокращенную суммарную кривую
Рис.17. Расчет многолетней составляющей полезного объема водохранилища на р.Ашлык по сокращенной суммарной кривой притока за 1954-1979 гг.
Расчетная группа лет (с 1954 по 1979 гг.) считается замкнутой по предположению, что она достаточно полно характеризует чередование групп многоводных и маловодных лет в рядах годового стока р.Ашлык у с.Ашлык. Практически это значит, что вслед за последним 1979 годом мы предполагаем появление такого же точно года, вернее гидрографа, какой был в начале расчетной группы лет, то есть 1954 г., затем 1955 г. и т.д. Это дает нам основание продолжить построение ССК влево (вниз) или, если это удобнее, вправо (вверх). Крутые участки кривых соответствуют многоводным или маловодным годам, пологие – близким к норме. Чтобы выделить наиболее глубокий и длительный период недостатков, определяющий полезный объем водохранилища, следует ССК начать строить не с начала таблицы, а от самой большой положительной ординаты (хотя она может оказаться в конце таблицы). Выносить ординаты на график следует по ходу времени до самой большой по абсолютной величине отрицательной ординаты (хотя она может оказаться в начале таблицы). При этом конец таблицы можно считать ее началом, то есть продолжать строить ССК, переходя от конца таблицы к ее началу. Перейдем теперь к построению ССК потребления. ССК потребления (рис.17) q=Q0 или Если RS=2, 5 см, MR=Р=1, 25 см. Разделим RS на 20 частей и соединим деления с точкой М. Получатся наклонные линии, соответствующие наклону ССК потребления при Во всех наиболее характерных точках перегиба кривой проводят касательные параллельно прямой потребления, чтобы выделить моменты времени, когда q=Q (то есть тангенсы углов наклона этих касательных и касательных, проведенных к ССК потребления, равны, а касательные к прямой всегда совпадают с ней). Таким путем можно найти начало и конец каждого периода избытков и недостатков. Чтобы подсчитать
где
n - число интервалов (лет)между точками касания, между точками В и А например, 21 год;
Подставим в формулу (21) ординаты пары точек В1 (или В11) и А, а затем точек О1 и А1 (см.табл. 13, графа 5):
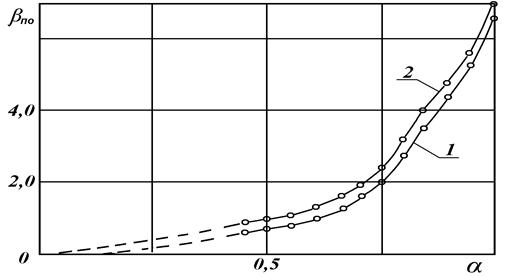
Наибольшее значение 5, 26 принимается за расчетное. При При расчете
Рис. 18. График зависимости (от коэффициента зарегулирования (
Таблица 14
|

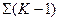
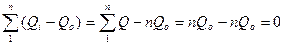
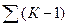 . ССК стока представлена на рис.17.
. ССК стока представлена на рис.17.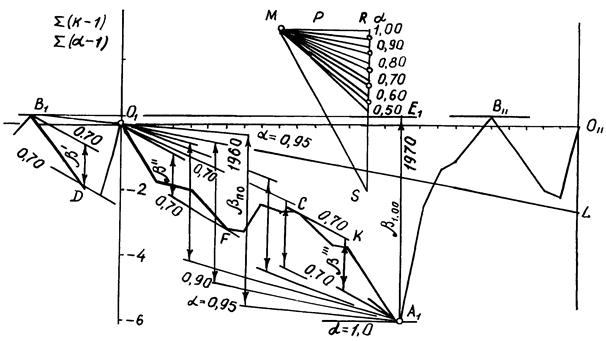
 =1 выразится линией О1О11, так как
=1 выразится линией О1О11, так как  при любом n. Если
при любом n. Если  . При
. При  и оси абсцисс mt можно построить в любом месте чертежа масштабный треугольник MRS, в котором сторона RS принята за единицу, а сторона MR (или полюсное расстояние Р) = m
и оси абсцисс mt можно построить в любом месте чертежа масштабный треугольник MRS, в котором сторона RS принята за единицу, а сторона MR (или полюсное расстояние Р) = m 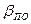 =5, 25, VПО=5, 25*129 млн.м3=677 млн.м3.
=5, 25, VПО=5, 25*129 млн.м3=677 млн.м3.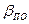 =
= 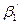 -
-  -n(1-
-n(1-  - ордината правой нижней точки касания;
- ордината правой нижней точки касания;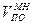 =5.26*129=680 млн.м3. При
=5.26*129=680 млн.м3. При  =f(
=f(