Этап 2: определение аппроксимирующей функции элементов
Эту процедуру можно выполнить один раз для типичного элемента области безотносительно к его топологическому положению в ней. Полученная функция используется далее для всех остальных элементов области того же вида. Эта особенность является важным аспектом МКЭ. Благодаря ней элементы с однажды определенными функциями легко включаются в библиотеку элементов соответствующего программного комплекса. Далее эти элементы применяются для решения разнообразных краевых задач. В качестве аппроксимирующих функций элементов чаще всего используются полиномы. В зависимости от степени полинома конечные элементы делятся на симплекс–, комплекс– и мультиплекс–элементы. Полиномы симплекс-элементов содержат константы и линейные члены; полиномы комплекс-элементов — константы, линейные члены, а также члены более высоких степеней. Комплекс-элементы, как правило, кроме граничных имеют дополнительные внутренние узлы. Полиномы мультиплекс-элементов также содержат члены более высоких степеней. На мультиплекс-элементы накладывается дополнительное условие: их границы должны быть параллельны координатным осям. Одномерный симплекс-элемент представляет собой отрезок, изображенный на рисунке 2.15.
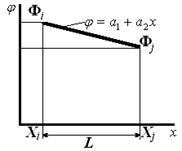
Рис. 2.15. Одномерный симплекс-элемент
При определении функции этого элемента для простоты будем считать, что узловые значения искомой непрерывной функции, определенные на концах отрезка, известны. По длине отрезка значение функции φ аппроксимируется полиномом: φ = α 1 + α 2х. (2.46)
Коэффициенты α 1 и α 2 определяются через узловые значения функции Фi и Фj в соответствии с условием непрерывности:
φ = Фi при х = Хi, φ = Фj при х = Хj. (2.47)
Подставив (2.47) в (2.46), получим систему уравнений:
Фi = α 1 + α 2 Хi, Фj = α 1 + α 2 Хj.
решая которую, определим α 1 и α 2:
т.е.
Подставив вычисленные значения коэффициентов аппроксимирующего полинома в (2.46), получим
Проведем эквивалентные преобразования правой части:
Члены полученного уравнения, заключенные в скобки, являются функциями формы одномерного симплекс–элемента:
С учетом обозначений (2.49) уравнение (2.48) принимает вид
φ = NiФi + NjФj, (2.50)
или в матричной форме
φ = NФ, (2.51)
где N = [Ni, Nj] — матрица–строка; Функция формы обладает следующим свойством: функция формы с номером i равна 1 в узле с соответствующим номером и равна 0 во всех других узлах. Не представляет труда убедиться в наличии этого свойства у функций формы (2.49). Двумерный симплекс–элемент представляет собой плоский треугольник с прямолинейными сторонами. Интерполяционный полином, аппроксимирующий непрерывную функцию φ внутри треугольного симплекс–элемента имеет вид
φ = a1 + a2x + a3y (2.52)
Чтобы получить выражения для функций формы элемента, необходимо пронумеровать узлы треугольника. Обозначим их номерами i, j, k, начиная с произвольно выбранного узла, двигаясь при этом против часовой стрелки (рис. 2.16). Узловые значения Фi, Фj, Фk будем по-прежнему считать известными.
Рис. 2.16. Функция двухмерного симплекс–элемента
Используя условие непрерывности искомой функции в узлах аналогично предыдущему случаю, составим систему уравнений
решая которую относительно неизвестных коэффициентов полинома, получим: a1 = (0, 5/ S[(XjYk – XkYj)Фi + (XkYi – XiYk)Фj + (XiYj – – XjYi)Фk]); a2 = (0, 5/ S)[(Yj – Yk)Фi + (Yk – Yi)Фj + (Yi – Yj)Фk]); a3 = (0, 5/ S)[(Xk – Xj)Фi + (Xi – Xk)Фj + (Xj – Xi)Фk]. (2.53)
где S — площадь элемента, вычисляемая по формуле
Подставим (2.53) в (2.52), проделаем аналогичные преобразования, получим
где и
Вычисляя значения функций формы Ni, Nj, Nk нетрудно убедиться, что они равны 1 в узлах с соответствующими номерами и 0 в остальных узлах элемента. Функции (2.50) для одномерного и (2.55) для двумерного симплекс–элементов были получены для типичных элементов безотносительно к положению в области. Поэтому они удовлетворяют всем элементам данного типа, что позволяет создавать обширные библиотеки элементов в САПР. Аналогично вычисляют функции всех прочих типов элементов.
|



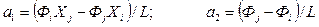 .
.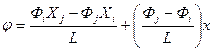 .
. (2.48)
(2.48)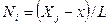 ;
;  . (2.49)
. (2.49)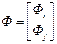 — вектор-столбец.
— вектор-столбец.

 .
. (2.54)
(2.54) (2.55)
(2.55)





