Оценка достоверности
Достоверность разности между двумя средними величинами определяется по формуле:
М1 и М2 – две средних арифметических величины, полученные в двух самостоятельных независимых группах наблюдений; m1 и m2 - их средние ошибки (выражение При t ≥ 2 разность средних арифметических может быть признана существенной и неслучайной, то есть достоверной. Это значит, что и в генеральной совокупности средние величины отличаются, и что при повторении подобных наблюдений будут получены аналогичные различия. При t = 2 надежность также увеличивается, а риск ошибки уменьшается. При t< 2 достоверность разности средних величин считается недоказанной.
Таблица t (критерии Стьюдента)
Достоверность разности показателей Использует формулу:
Р – показатель m – ошибка показателя Достоверность показателя определяется с помощью его средней ошибки по формуле:
|
, где
называют средней ошибкой разности двух средних).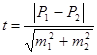
, где
, где р – размер показателя, выраженный в долях единицы, в процентах, в промилле; q – равно 1-p или 100-p или 1000-р (величина, дополняющая показатель до основания); n – число наблюдений.
