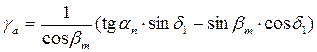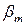12.1 Ориентировочное (первое приближение) значение внешнего делительного диаметра шестерни, мм:
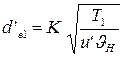
Здесь К = 30 при 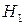 и
и 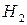 ≤ 350 НВ;
≤ 350 НВ;
К = 25 при 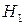 ≥ 45 HRC и
≥ 45 HRC и 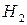 ≤ 350 НВ;
≤ 350 НВ;
К = 22 при 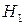 и
и 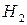 ≥ 45 HRC.
≥ 45 HRC.
Коэффициент 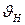 учитывающий вид конической передачи, выбирают по табл. 12.1.
учитывающий вид конической передачи, выбирают по табл. 12.1.
Таблица 12.1
Значения коэффициентов 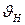 и
и 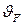 для передач с круговыми зубьями
для передач с круговыми зубьями
| Твердость зубчатых колес
| 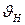
| 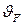
|
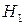 и и 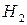 ≤ 350 НВ ≤ 350 НВ
| 1, 22+0, 21× u
| 0, 94+0, 08× u
|
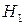 ≥ 45 HRC и ≥ 45 HRC и 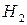 ≤ 350 НВ ≤ 350 НВ
| 1, 13+0, 13× u
| 0, 85+0, 04× u
|
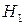 и и 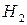 ≥ 45 HRC ≥ 45 HRC
| 0, 81+0, 15× u
| 0, 65+0, 11× u
|
Примечание: Для прямозубых конических передач 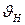 =
= 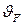 = 0, 85.
= 0, 85.
12.2 Ориентировочное значение средней окружной скорости (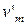 , м/с) вычисляют по следующей зависимости:
, м/с) вычисляют по следующей зависимости:
 при
при  = 0, 285.
= 0, 285.
12.3 Необходимую степень точности передачи назначают в зависимости от окружной скорости. Прямозубые конические колеса применяют при  < 5 м/сек, степень точности их изготовления в этом случае должна быть не более 7 - й. Конические зубчатые колеса с круговыми зубьями при
< 5 м/сек, степень точности их изготовления в этом случае должна быть не более 7 - й. Конические зубчатые колеса с круговыми зубьями при  < 5 м/сек выполняют не менее 8-й степени точности, а при
< 5 м/сек выполняют не менее 8-й степени точности, а при  = 5...10 м/сек – не менее 7-й.
= 5...10 м/сек – не менее 7-й.
12.4 Предварительное (при втором приближении) значение внешнего делительного диаметра шестерни 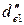 , мм:
, мм:
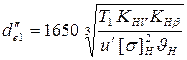 .
.
12.5 Значение коэффициента динамической нагрузки  для передач с круговыми зубьями выбирают такое же, как и для цилиндрических косозубых передач (см. табл. 8.1). Для конических прямозубых передач значение
для передач с круговыми зубьями выбирают такое же, как и для цилиндрических косозубых передач (см. табл. 8.1). Для конических прямозубых передач значение  выбирают также по табл. 8.1, но при этом точность условно берут на одну степень меньше фактической.
выбирают также по табл. 8.1, но при этом точность условно берут на одну степень меньше фактической.
Коэффициент  , учитывающий неравномерность распределения нагрузки по длине контактных линий для колес с круговыми зубьями, определяют по формуле:
, учитывающий неравномерность распределения нагрузки по длине контактных линий для колес с круговыми зубьями, определяют по формуле:

где 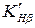 – коэффициент, выбираемый по графикам (см. рис. 8.1) в зависимости от отношения
– коэффициент, выбираемый по графикам (см. рис. 8.1) в зависимости от отношения 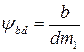 , твердости зубчатых колес и схемы передачи.
, твердости зубчатых колес и схемы передачи.
Для большинства конических передач при передаточных числах u ≤ 5 отношение ширины зубчатого венца (длины зуба) к внешнему конусному расстоянию 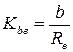 = 0, 285, и тогда:
= 0, 285, и тогда:

Для прямозубых конических передач  выбирают по графикам (рис. 8.1).
выбирают по графикам (рис. 8.1).
12.6 Допускаемое напряжение  – для передач с прямыми и круговыми зубьями, твердость которых больше 350 НВ, равно меньшему из допускаемых напряжений шестерни
– для передач с прямыми и круговыми зубьями, твердость которых больше 350 НВ, равно меньшему из допускаемых напряжений шестерни  и колеса
и колеса 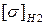 :
:
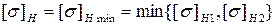
Для передач с круговыми зубьями, у которых твердость колеса 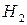 ≤ 350 НВ, и любой твердости шестерни:
≤ 350 НВ, и любой твердости шестерни:

При этом должно выполняться условие:
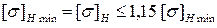
Допускаемые напряжения  и
и 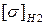 определяют по общей зависимости:
определяют по общей зависимости:
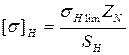
где  – см. табл. 6.1;
– см. табл. 6.1;
 – см. табл. 6.2;
– см. табл. 6.2;
 – см. п. 6.1.
– см. п. 6.1.
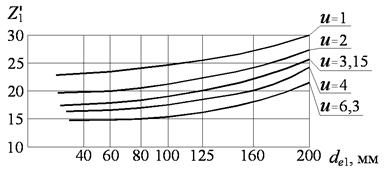
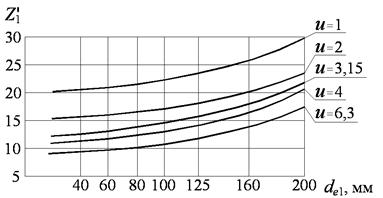
12.7 Предварительное значение числа зубьев шестерни 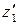 выбирают в зависимости от ее диаметра и вида передачи по графикам, приведенным на рис. 12.2 (а - прямозубые шестерни, б - шестерни с круговыми зубьями). Далее это число зубьев уточняют.
выбирают в зависимости от ее диаметра и вида передачи по графикам, приведенным на рис. 12.2 (а - прямозубые шестерни, б - шестерни с круговыми зубьями). Далее это число зубьев уточняют.
 а
а
|
 б
б
|
| Рис. 12.2. График для определения числа зубьев:
а - прямозубая шестерня, б - шестерня с круговыми зубьями
|
Ниже даны соотношения между предварительным и окончательным числом зубьев шестерни для колес различной твердости:
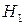 и
и 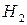 ≥ 45 HRC,
≥ 45 HRC,  ;
;
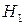 ≥ 45 HRC и
≥ 45 HRC и 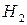 ≤ 350 НВ,
≤ 350 НВ,  ;
;
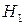 и
и 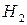 ≤ 350 НВ,
≤ 350 НВ, 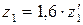 ;
;
Полученное значение  , округляют до целого.
, округляют до целого.
Вычисляют число зубьев колеса по формуле (с округлением до целого): 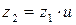 .
.
12.8 Определяют окончательное значение передаточного числа:
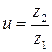 .
.
Для силовых редукторов окончательное значение 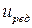 не должно отличаться от заданного не более чем на 4 %.
не должно отличаться от заданного не более чем на 4 %.
12.9 Вычисляют углы делительных конусов, °:
 ,
, 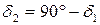
с точностью не менее 0, 003°.
12.10 Внешний окружной модуль ( ,
, 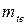 , мм) для прямозубых зубчатых колес и колес с круговыми зубьями определяют соответственно по формулам
, мм) для прямозубых зубчатых колес и колес с круговыми зубьями определяют соответственно по формулам
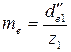 и
и 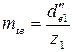 .
.
Внешний окружной модуль разрешается не округлять до стандартного значения (ГОСТ 9563-60), так как одним и тем же режущим инструментом можно нарезать колеса с различными значениями модуля, лежащими в некотором непрерывном интервале.
Точность вычислений  и
и 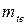 должна быть не менее 0, 0001 мм. Принимать внешний окружной модуль для силовых зубчатых передач менее 1 мм нежелательно.
должна быть не менее 0, 0001 мм. Принимать внешний окружной модуль для силовых зубчатых передач менее 1 мм нежелательно.
12.11 Рассчитывают внешнее конусное расстояние ( , мм) для прямозубых зубчатых колес и колес с круговыми зубьями:
, мм) для прямозубых зубчатых колес и колес с круговыми зубьями:
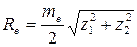 и
и 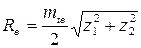
соответственно. Значение  не округляют.
не округляют.
12.12 Определяют ширину зубчатых венцов колес (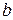 , мм):
, мм):

Вычисленное значение 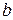 округляют до целого числа.
округляют до целого числа.
12.13 Находят значение коэффициента смещения зуборезного инструмента по табл. 12.2 и 12.3 в зависимости от числа зубьев шестерни и передаточного числа зубчатой пары.
Коэффициенты смещения инструмента для колеса принимают 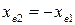 , если шестерня прямозубая, и
, если шестерня прямозубая, и 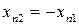 если шестерня с круговыми зубьями.
если шестерня с круговыми зубьями.
Таблица 12.2
Коэффициент смещения 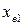 для шестерен с прямыми зубьями
для шестерен с прямыми зубьями
(ГОСТ 19624-74)

| 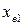 при u при u
|
| 1, 0
| 1, 25
| 1, 6
| 2, 0
| 2, 5
| 3, 15
| 4, 0
| 5, 0
|
|
| –
| –
| –
| –
| 0, 50
| 0, 53
| 0, 56
| 0, 57
|
|
| –
| –
| –
| 0, 44
| 0, 48
| 0, 52
| 0, 54
| 0, 55
|
|
| –
| –
| 0, 34
| 0, 42
| 0, 47
| 0, 50
| 0, 52
| 0, 53
|
|
| –
| 0, 18
| 0, 31
| 0, 40
| 0, 45
| 0, 48
| 0, 50
| 0, 51
|
|
| –
| 0, 17
| 0, 30
| 0, 38
| 0, 43
| 0, 46
| 0, 48
| 0, 49
|
|
|
| 0, 15
| 0, 28
| 0, 36
| 0, 40
| 0, 43
| 0, 45
| 0, 46
|
|
|
| 0, 14
| 0, 26
| 0, 34
| 0, 37
| 0, 40
| 0, 42
| 0, 43
|
|
|
| 0, 13
| 0, 23
| 0, 29
| 0, 33
| 0, 36
| 0, 38
| 0, 39
|
|
|
| 0, 11
| 0, 19
| 0, 25
| 0, 28
| 0, 31
| 0, 33
| 0, 34
|
|
|
| 0, 09
| 0, 15
| 0, 20
| 0, 22
| 0, 24
| 0, 26
| 0, 27
|
Примечание: Для передач, у которых значения z и u отличается от указанных в таблице, коэффициент 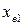 , принимают с округлением в большую сторону.
, принимают с округлением в большую сторону.
Таблица 12.3
Коэффициент смещения  для шестерен с круговыми зубьями
для шестерен с круговыми зубьями
(ГОСТ 19326-73)
| z
|  при u при u
|
| 1, 0
| 1, 25
| 1, 6
| 2, 0
| 2, 5
| 3, 15
| 4, 0
| 5, 0
|
|
| –
| –
| –
| 0, 32
| 0, 37
| 0, 39
| 0, 41
| 0, 42
|
|
| –
| –
| –
| 0, 30
| 0, 35
| 0, 37
| 0, 39
| 0, 40
|
|
| –
| –
| 0, 23
| 0, 29
| 0, 33
| 0, 35
| 0, 37
| 0, 38
|
|
| –
| 0, 12
| 0, 22
| 0, 27
| 0, 31
| 0, 33
| 0, 35
| 0, 36
|
|
| –
| 0, 11
| 0, 21
| 0, 26
| 0, 30
| 0, 32
| 0, 34
| 0, 35
|
|
|
| 0, 10
| 0, 19
| 0, 24
| 0, 27
| 0, 30
| 0, 32
| 0, 32
|
|
|
| 0, 09
| 0, 17
| 0, 22
| 0, 26
| 0, 28
| 0, 29
| 0, 29
|
|
|
| 0, 08
| 0, 15
| 0, 19
| 0, 21
| 0, 24
| 0, 25
| 0, 25
|
|
|
| 0, 07
| 0, 11
| 0, 16
| 0, 18
| 0, 21
| 0, 22
| 0, 22
|
|
|
| 0, 05
| 0, 09
| 0, 11
| 0, 14
| 0, 16
| 0, 17
| 0, 17
|
Примечание: Для передач, у которых значения  и u отличаются от указанных в таблице, коэффициент
и u отличаются от указанных в таблице, коэффициент  принимают с округлением в большую сторону.
принимают с округлением в большую сторону.
12.14 Геометрические размеры конической зубчатой передачи (внешний делительный диаметр, внешний диаметр вершин зубьев, средний нормальный модуль) определяют по табл. 12.4.
Таблица 12.4
Определение геометрических параметров конической зубчатой передачи
| Параметр
| Расчетная формула для передач
|
| прямозубых
| с круговыми зубьями
|
| Внешний делительный диаметр
| 
| 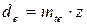
|
| Внешний диаметр вершин зубьев
| 
| 
|
| Средние окружной и нормальный модули
| 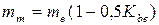
| 
|
| Средний делительный диаметр
| 
| 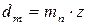
|
| Эквивалентное и биэквивалентное числа зубьев
| 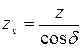
|  при
при 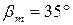
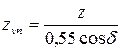
|
Примечания: 1. Номинальные значения внешних делительных диаметров  ведомых конических колес в редукторах общемашиностроительного применения принимаются из ряда (ГОСТ 27142-97): 50, (56), 63, (71), 80, (90), 100, (112), 125, (140), 160, (180), 200, (224), 250, (280), 315, (355), 400, (450), 500, (560), 630, (710), 800, (900), 1000. Значение без скобок являются предпочтительными. Фактические значения диаметров не должны отличаться от номинальных более чем на ±6%.
2. В многоступенчатых редукторах соотношение внешнего делительного диаметра ведомых конических колес в редукторах общемашиностроительного применения принимаются из ряда (ГОСТ 27142-97): 50, (56), 63, (71), 80, (90), 100, (112), 125, (140), 160, (180), 200, (224), 250, (280), 315, (355), 400, (450), 500, (560), 630, (710), 800, (900), 1000. Значение без скобок являются предпочтительными. Фактические значения диаметров не должны отличаться от номинальных более чем на ±6%.
2. В многоступенчатых редукторах соотношение внешнего делительного диаметра  конической передачи с межосевым расстоянием последующей цилиндрической передачи рекомендуется принимать 1, 4…1, 6.
3. В редукторах общемашиностроительного применения средний нормальный модуль конической передачи с межосевым расстоянием последующей цилиндрической передачи рекомендуется принимать 1, 4…1, 6.
3. В редукторах общемашиностроительного применения средний нормальный модуль  для конических передач с круговыми зубьями и внешний окружной модуль для конических передач с круговыми зубьями и внешний окружной модуль 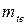 для конических передач с прямыми зубьями рекомендуется принимать по ГОСТ 9563 в диапазоне для конических передач с прямыми зубьями рекомендуется принимать по ГОСТ 9563 в диапазоне 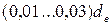 , при этом меньшие значения соответствуют большим передаточным числам ступени, большие – малым. , при этом меньшие значения соответствуют большим передаточным числам ступени, большие – малым.
|
12.15 Для проверки возможности получения при термической обработке требуемых механических характеристик вычерчивают эскизы заготовок зубчатых колес (см. рис. 5.1). Если размеры D или 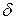 сечения заготовок больше, чем те, при которых можно обеспечить требуемые механические характеристики материала заготовок, то выбирают другую марку стали или изменяют размеры заготовок.
сечения заготовок больше, чем те, при которых можно обеспечить требуемые механические характеристики материала заготовок, то выбирают другую марку стали или изменяют размеры заготовок.
12.16 Проверка зубчатой передачи на контактную выносливость:
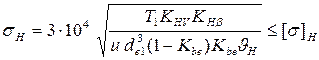 .
.
Если передача выполнена с отношением длины зуба к внешнему конусному расстоянию  = 0, 285, то возможно использовать более простую зависимость:
= 0, 285, то возможно использовать более простую зависимость:
 .
.
Примечание: Эту проверку выполняют только в тех случаях, когда при проработке конструкции колес размеры их были изменены по сравнению с ранее полученными.
12.17 Проверку зубчатой передачи на выносливость при изгибе проводят для зубьев шестерни ( ) и колеса (
) и колеса (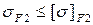 ) по общей зависимости:
) по общей зависимости:
 .
.
Коэффициент динамической нагрузки 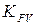 выбирают по табл. 8.1 в зависимости от тех же факторов, что и при выборе
выбирают по табл. 8.1 в зависимости от тех же факторов, что и при выборе  .
.
Коэффициент  , учитывающий неравномерность распределения нагрузки по длине контактных линий, для колес с круговыми зубьями составляет:
, учитывающий неравномерность распределения нагрузки по длине контактных линий, для колес с круговыми зубьями составляет:
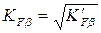 ³ 1, 15,
³ 1, 15,
где 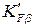 , определяют по графикам (см. рис. 8.1).
, определяют по графикам (см. рис. 8.1).
Для прямозубых: конических передач  выбирают по графикам (см. рис. 8.1): схема 1, если опоры вала шестерни выполнены на шариковых радиально-упорных подшипниках; схема 2 - при роликовых радиально-упорных конических подшипниках.
выбирают по графикам (см. рис. 8.1): схема 1, если опоры вала шестерни выполнены на шариковых радиально-упорных подшипниках; схема 2 - при роликовых радиально-упорных конических подшипниках.
Коэффициент 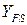 , учитывающий форму зуба и концентрацию напряжений, определяют по рис. 9.2 в зависимости от эквивалентного числа зубьев
, учитывающий форму зуба и концентрацию напряжений, определяют по рис. 9.2 в зависимости от эквивалентного числа зубьев  или биэквивалвнтного
или биэквивалвнтного  (см. табл. 12.4) и коэффициента смещения инструмента
(см. табл. 12.4) и коэффициента смещения инструмента  (прямозубые колеса) или
(прямозубые колеса) или  (колеса с круговыми зубьями).
(колеса с круговыми зубьями).
Коэффициент 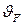 , учитывающий вид передачи, выбирают по табл. 12.1. Допускаемые напряжения шестерни
, учитывающий вид передачи, выбирают по табл. 12.1. Допускаемые напряжения шестерни  и колеса
и колеса  определяют по общей зависимости:
определяют по общей зависимости:
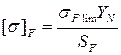 ,
,
где  – см. табл. 6.3;
– см. табл. 6.3;  и
и  – см. п. 6.2.
– см. п. 6.2.
12.18 Проверка зубчатой передачи на прочность при действии пиковой нагрузки. Методику расчета см. в п. 9.12, 6.3, 9.13, 6.4.

|
| Рис. 19. Схема сил, действующих на валы от зубчатых колес
в конической передаче
|
12.19 Силы, действующие на валы конических зубчатых колес, определяют следующим образом (см. рис. 12.3):
окружная сила на шестерне:
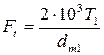 ;
;
осевая сила на шестерне прямозубой передачи и передачи с круговыми зубьями:
 и
и 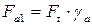
соответственно;
радиальная сила на шестерне прямозубой передачи и передачи с круговыми зубьями:
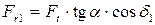 и
и 
соответственно;
осевая сила на колесе:
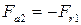 ;
;
радиальная сила на колесе:
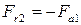 ;
;
В последних двух выражениях знак " минус" указывает, что обе силы имеют противоположное направление. При расчете осевой и радиальной сил коэффициенты 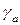 и
и  (табл. 12.5) подставляют в формулы со своими знаками. Наклон зуба шестерни выбирает таким, чтобы сила
(табл. 12.5) подставляют в формулы со своими знаками. Наклон зуба шестерни выбирает таким, чтобы сила 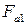 была направлена к основанию конуса.
была направлена к основанию конуса.
Для обеспечения этого условия, если шестерня является ведущей, следует выбирать направление наклона зуба (смотря со стороны вершины делительного конуса) одинаковым с направлением вращения и противоположным, если шестерня ведомая.
Таблица 12.5
Формулы для расчета коэффициентов осевой и радиальной сил
| Схема шестерни
| Направление
| Формулы для расчета
|
| вращения
| линии зуба
|

| по часовой стрелке (правое)
| правое
| 
|

| против часовой стрелки (левое)
| левое
| 
|

| против часовой стрелки (левое)
| правое
| 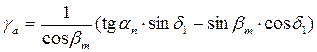
|

| по часовой стрелке (правое)
| левое
| 
|
12.20 Результаты проектного расчета, необходимые для разработки чертежей конических зубчатых колес, представляют в виде табл. 12.6 и 12.7.
Таблица 12.6
Колеса с круговыми зубьями
| Параметр
| Обозначение
| Значение параметра для
|
| шестерни
| колеса
|
| Средний нормальный модуль
| 
|
|
|
| Число зубьев
| z
|
|
|
| Средний угол наклона зуба
| 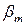
|
|
|
| Направление линии зуба
| –
|
|
|
| Стандарт на исходный контур
| –
| ГОСТ 16202-70
|
| Коэффициент смещения
| 
|
|
|
| Угол делительного конуса
| 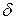
|
|
|
| Степень точности по ГОСТ 1758-81
| –
|
|
|
Таблица 12.7
Прямозубые колеса
| Параметр
| Обозначение
| Значение параметра для
|
| шестерни
| колеса
|
| Средний окружной модуль
| 
|
|
|
| Число зубьев
| z
|
|
|
| Стандарт на исходный контур
| –
| ГОСТ 13754-61
|
| Коэффициент смещения
| 
|
|
|
| Угол делительного конуса
| 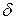
|
|
|
| Степень точности по ГОСТ 1758-81
| –
|
|
|

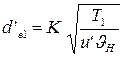
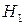 и
и 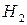 ≤ 350 НВ;
≤ 350 НВ;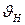 учитывающий вид конической передачи, выбирают по табл. 12.1.
учитывающий вид конической передачи, выбирают по табл. 12.1.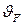 для передач с круговыми зубьями
для передач с круговыми зубьями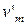 , м/с) вычисляют по следующей зависимости:
, м/с) вычисляют по следующей зависимости: при
при  = 0, 285.
= 0, 285. < 5 м/сек, степень точности их изготовления в этом случае должна быть не более 7 - й. Конические зубчатые колеса с круговыми зубьями при
< 5 м/сек, степень точности их изготовления в этом случае должна быть не более 7 - й. Конические зубчатые колеса с круговыми зубьями при 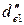 , мм:
, мм: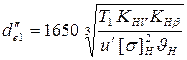 .
. для передач с круговыми зубьями выбирают такое же, как и для цилиндрических косозубых передач (см. табл. 8.1). Для конических прямозубых передач значение
для передач с круговыми зубьями выбирают такое же, как и для цилиндрических косозубых передач (см. табл. 8.1). Для конических прямозубых передач значение  , учитывающий неравномерность распределения нагрузки по длине контактных линий для колес с круговыми зубьями, определяют по формуле:
, учитывающий неравномерность распределения нагрузки по длине контактных линий для колес с круговыми зубьями, определяют по формуле:
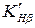 – коэффициент, выбираемый по графикам (см. рис. 8.1) в зависимости от отношения
– коэффициент, выбираемый по графикам (см. рис. 8.1) в зависимости от отношения 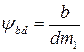 , твердости зубчатых колес и схемы передачи.
, твердости зубчатых колес и схемы передачи.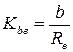 = 0, 285, и тогда:
= 0, 285, и тогда:
 – для передач с прямыми и круговыми зубьями, твердость которых больше 350 НВ, равно меньшему из допускаемых напряжений шестерни
– для передач с прямыми и круговыми зубьями, твердость которых больше 350 НВ, равно меньшему из допускаемых напряжений шестерни  и колеса
и колеса 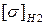 :
: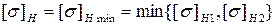

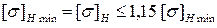
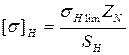
 – см. табл. 6.1;
– см. табл. 6.1; – см. табл. 6.2;
– см. табл. 6.2; – см. п. 6.1.
– см. п. 6.1.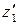 выбирают в зависимости от ее диаметра и вида передачи по графикам, приведенным на рис. 12.2 (а - прямозубые шестерни, б - шестерни с круговыми зубьями). Далее это число зубьев уточняют.
выбирают в зависимости от ее диаметра и вида передачи по графикам, приведенным на рис. 12.2 (а - прямозубые шестерни, б - шестерни с круговыми зубьями). Далее это число зубьев уточняют. а
а
 б
б
 ;
; ;
;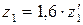 ;
; , округляют до целого.
, округляют до целого.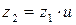 .
.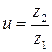 .
.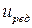 не должно отличаться от заданного не более чем на 4 %.
не должно отличаться от заданного не более чем на 4 %. ,
, 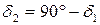
 ,
, 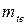 , мм) для прямозубых зубчатых колес и колес с круговыми зубьями определяют соответственно по формулам
, мм) для прямозубых зубчатых колес и колес с круговыми зубьями определяют соответственно по формулам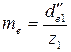 и
и 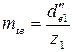 .
. , мм) для прямозубых зубчатых колес и колес с круговыми зубьями:
, мм) для прямозубых зубчатых колес и колес с круговыми зубьями: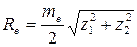 и
и 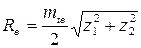
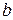 , мм):
, мм):
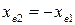 , если шестерня прямозубая, и
, если шестерня прямозубая, и 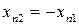 если шестерня с круговыми зубьями.
если шестерня с круговыми зубьями.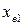 для шестерен с прямыми зубьями
для шестерен с прямыми зубьями для шестерен с круговыми зубьями
для шестерен с круговыми зубьями и u отличаются от указанных в таблице, коэффициент
и u отличаются от указанных в таблице, коэффициент 
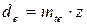


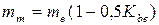


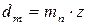
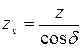
 при
при 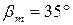
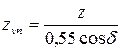
 ведомых конических колес в редукторах общемашиностроительного применения принимаются из ряда (ГОСТ 27142-97): 50, (56), 63, (71), 80, (90), 100, (112), 125, (140), 160, (180), 200, (224), 250, (280), 315, (355), 400, (450), 500, (560), 630, (710), 800, (900), 1000. Значение без скобок являются предпочтительными. Фактические значения диаметров не должны отличаться от номинальных более чем на ±6%.
2. В многоступенчатых редукторах соотношение внешнего делительного диаметра
ведомых конических колес в редукторах общемашиностроительного применения принимаются из ряда (ГОСТ 27142-97): 50, (56), 63, (71), 80, (90), 100, (112), 125, (140), 160, (180), 200, (224), 250, (280), 315, (355), 400, (450), 500, (560), 630, (710), 800, (900), 1000. Значение без скобок являются предпочтительными. Фактические значения диаметров не должны отличаться от номинальных более чем на ±6%.
2. В многоступенчатых редукторах соотношение внешнего делительного диаметра  для конических передач с круговыми зубьями и внешний окружной модуль
для конических передач с круговыми зубьями и внешний окружной модуль 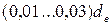 , при этом меньшие значения соответствуют большим передаточным числам ступени, большие – малым.
, при этом меньшие значения соответствуют большим передаточным числам ступени, большие – малым.
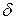 сечения заготовок больше, чем те, при которых можно обеспечить требуемые механические характеристики материала заготовок, то выбирают другую марку стали или изменяют размеры заготовок.
сечения заготовок больше, чем те, при которых можно обеспечить требуемые механические характеристики материала заготовок, то выбирают другую марку стали или изменяют размеры заготовок.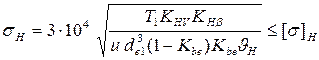 .
. .
. ) и колеса (
) и колеса (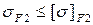 ) по общей зависимости:
) по общей зависимости: .
.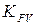 выбирают по табл. 8.1 в зависимости от тех же факторов, что и при выборе
выбирают по табл. 8.1 в зависимости от тех же факторов, что и при выборе  , учитывающий неравномерность распределения нагрузки по длине контактных линий, для колес с круговыми зубьями составляет:
, учитывающий неравномерность распределения нагрузки по длине контактных линий, для колес с круговыми зубьями составляет: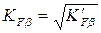 ³ 1, 15,
³ 1, 15,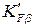 , определяют по графикам (см. рис. 8.1).
, определяют по графикам (см. рис. 8.1).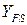 , учитывающий форму зуба и концентрацию напряжений, определяют по рис. 9.2 в зависимости от эквивалентного числа зубьев
, учитывающий форму зуба и концентрацию напряжений, определяют по рис. 9.2 в зависимости от эквивалентного числа зубьев  или биэквивалвнтного
или биэквивалвнтного  (см. табл. 12.4) и коэффициента смещения инструмента
(см. табл. 12.4) и коэффициента смещения инструмента  (прямозубые колеса) или
(прямозубые колеса) или  (колеса с круговыми зубьями).
(колеса с круговыми зубьями). и колеса
и колеса  определяют по общей зависимости:
определяют по общей зависимости: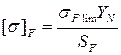 ,
, – см. табл. 6.3;
– см. табл. 6.3;  и
и  – см. п. 6.2.
– см. п. 6.2.
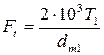 ;
; и
и 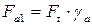
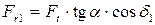 и
и 
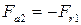 ;
;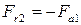 ;
;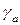 и
и  (табл. 12.5) подставляют в формулы со своими знаками. Наклон зуба шестерни выбирает таким, чтобы сила
(табл. 12.5) подставляют в формулы со своими знаками. Наклон зуба шестерни выбирает таким, чтобы сила 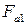 была направлена к основанию конуса.
была направлена к основанию конуса.