МЕХАНИКА. Дезинфекция,или обеззараживание, — это комплекс специальных мероприятий, направленных на уничтожение возбудителей заразных заболеваний в окружающей человека
МЕХАНИКА
ЛАБОРАТОРНАЯ РАБОТА № 5
определение момента инерции с помощью маятника обербека
САНКТ-ПЕТЕРБУРГ 2011 г.
Цель работы - исследовать зависимость момента инерции крестовины с надетыми на нее грузиками от распределения массы относительно оси вращения, проходящей через центр масс. Общие сведения
В основе эксперимента лежит основное уравнение динамики вращательного движения твердого тела
где В динамике вращательного движения различают два понятия: момент силы относительно точки и момент силы относительно оси вращения. Момент силы относительно точки О определяется как векторное произведение
где Момент силы относительно оси вращения есть проекция
Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от распределения массы тела относительно оси вращения. Для вычисления момента инерции твердого тела относительно данной оси разобьем мысленно тело на большое число весьма малых элементов - материальных точек (рис.1). Тогда момент инерции тела
или
где D mi - масса элемента; ri - расстояние от элемента до оси вращения; r - плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения. Таким образом, задача нахождения момента инерции сводится к интегрированию.
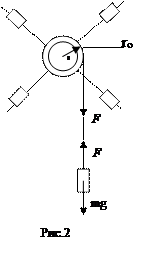
Маятник Обербека состоит из крестовины, на стержнях которой находятся грузы. Они могут перемещаться по стержням и закрепляться в нужном положении (рис.2). Крестовина с грузами насажена на вал, на котором укреплены два шкива различного радиуса. На шкив намотана нить, которая переброшена через блок. К ее концу привязана гирька, момент силы тяжести которой уравновешивает момент сил трения (вес этой гирьки в расчетах не учитывается). К концу нити подвешивают груз массой m, под действием силы тяжести которого система приводится в движение. На груз действует сила тяжести P= mg и сила натяжения F, поэтому на основании второго закона Ньютона можно записать
где g - ускорение свободного падения; а - ускорение, с которым движется груз. Крестовина приходит во вращательное движение под действием момента силы натяжения М = Fr о, (3) где r о - радиус шкива. Из уравнений (1)-(3) можно получить
Так как угловое ускорение связано с ускорением а соотношением e = а/r 0, то формулу (4) можно записать в виде
где а = 2 h/t 2; h - путь, пройденный грузом за время t. Таким образом,
Порядок выполнения работы Проверить, что две неподвижные рамки установлены на вертикальной линейке на расстоянии 40 – 50 см друг от друга. Измерить радиус шкива r 0. Последовательность проведения измерений следующая: 1) установить грузы на стержнях на максимальном расстоянии от оси вращения и закрепить их; 2) намотать нить на шкив, установив подвешенный груз на уровне верхней рамки; 3) отпустить груз и измерить время t его движения до нижней рамки (взять не менее трех отсчетов t и вычислить 4) сместить грузы на стержнях на два деления к центру и повторить пп.1-3, измерить расстояние r от оси вращения до центра масс груза; 5) повторить пп.4 для 8-10 положений грузов. Результаты измерений удобно представить в виде табл.1. Таблица 1
Примечание. J э рассчитывается по формуле (6).
Из теоретических соображений следует, что момент инерции крестовины с четырьмя грузами массой
где J 0 - момент инерции тела при r = 0. Из формулы (7) следует, что J = f (r2). Следовательно, если построить график этой функции в координатах J - r 2, то должна получиться прямая, продолжение которой будет пересекать ось ординат в некоторой точке, соответствующей J 0. Такое построение можно сделать приближенно, «на глаз». Однако математические методы обработки результатов наблюдения позволяют сделать такое построение достаточно точным. Наиболее просто это можно сделать, с помощью метода наименьших квадратов, вычислив J 0 и Для удобства перепишем формулу (7) в виде
где r2 = х и 4 m ' = b. Метод наименьших квадратов позволяет найти J 0 и b:
где Обработку результатов эксперимента удобно вести в форме табл.2. Таблица 2
Среднее квадратичное отклонение
По данным опыта и расчетов следует построить график функции в координатах J - r 2 (8), полученный методом наименьших квадратов, и вычислить доверительный интервал измерения момента инерции в границах
Контрольные вопросы 1. Что такое момент инерции? От чего он зависит? Как можно рассчитать момент инерции? 2. В чем заключается основное уравнение динамики вращательного движения? Что такое момент силы? 3. Что должно измениться в формуле (6), если изменить массу груза m и радиус шкива r 0? 4. Как выглядит график зависимости момента инерции в координатах J - r 2; J - r? Почему результаты опыта лучше обрабатывать в координатах J - r 2? 5. Почему график зависимости J = f (r 2) не проходит через начало координат? Какой смысл имеет величина J 0? 6. Какой смысл имеет тангенс угла наклона графика к горизонтальной оси?
|

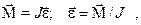 (1)
(1)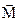 - суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси;
- суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси; 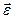 - угловое ускорение.
- угловое ускорение. ,
,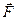 - сила,
- сила, 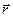 - радиус-вектор, проведенный из точки О, в точку приложения силы.
- радиус-вектор, проведенный из точки О, в точку приложения силы.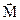 на произвольную ось z, которая проходит через точку О:
на произвольную ось z, которая проходит через точку О: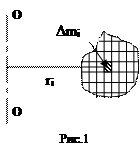
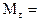
 .
.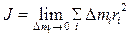
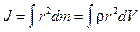 ,
, Из формулы (1) следует, что угловое ускорение e вращающегося тела прямо пропорционально моменту внешних сил М и обратно пропорционально моменту инерции J. Следует подчеркнуть, что момент инерции не зависит ни от момента внешних сил М, ни от углового ускорения.
Из формулы (1) следует, что угловое ускорение e вращающегося тела прямо пропорционально моменту внешних сил М и обратно пропорционально моменту инерции J. Следует подчеркнуть, что момент инерции не зависит ни от момента внешних сил М, ни от углового ускорения.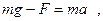 (2)
(2)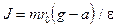 , (4)
, (4)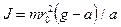 , (5)
, (5)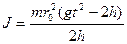 (6)
(6)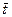 );
);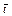
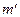 , если считать грузы материальными точками, можно выразить формулой
, если считать грузы материальными точками, можно выразить формулой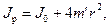 (7)
(7)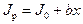 , (8)
, (8)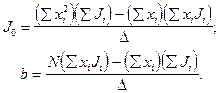 (9)
(9)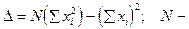 число опытов; Ji - экспериментальное значение момента инерции J э, полученное для каждого опыта (табл.1).
число опытов; Ji - экспериментальное значение момента инерции J э, полученное для каждого опыта (табл.1).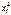
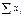
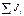
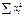
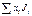
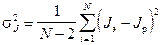 .
. .
.


