Екатеринбург 2009
Задания и методические указания для выполнения контрольной работы по дисциплине "Математика" (ГОС–2000). Екатеринбург, ГОУ ВПО «Российский государственный профессионально-педагогический университет», 2009. 18 с.
Составитель ст. преподаватель Танана Д.Б.
Рабочая программа одобрена на заседании кафедры высшей математики. Протокол от 23.04.09, № 9.
Заведующий кафедрой Е.А.Перминов
Рекомендована к печати методической комиссией машиностроительного факультета МаИ РГППУ. Протокол от 18.05.09, № 7.
Председатель методической комиссии МаИ РГППУ А.В.Песков
© ГОУ ВПО «Российский государственный профессионально-педагогический университет, 2009
Цель контрольных работ – закрепление и проверка знаний, полученных студентами в процессе самостоятельного изучения учебного материала по данной дисциплине, а также выявление их умения применять полученные знания на практике. Каждый студент заочной формы обучения должен выполнить все задачи своего варианта. При выполнении контрольных работ необходимо руководствоваться следующими требованиями: 1. Вариант контрольной работы следует выбирать по последней цифре номера зачетной книжки. 2. В начале работы должен быть указан номер варианта задания. 3. Перед решением задачи должно быть приведено ее условие. 4. Решение задач следует сопровождать необходимыми формулами, развернутыми расчетами и краткими пояснениями. 5. В конце работы должна стоять подпись студента с указанием даты ее выполнения. 6. На титульном листе контрольной работы необходимо указать следующую информацию: фамилию, имя и отчество студента; номер группы с указанием формы обучения; институт; факультет; дисциплину; номер зачетной книжки. Студенты, обучающиеся по полному сроку (5 лет 4 мес.) выполняют три контрольные работы; студенты, обучающиеся по сокращенному сроку (3,5 года) выполняют две контрольные работы. Номера задач, входящих в каждый из вариантов контрольной работы, приведены в следующей таблице.
Содержание контрольной работы 1-10. Даны векторы 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11-20. Дана система линейных уравнений: 11. 13. 15. 17. 19.
21-25. Построить график функции 21. 23. 25. 26-30. Построить график функции 26. 28. 30. 31-40. Найти производные 31. а) в) 32. а) г) 33. а) г)
34. а) в) 35. а) г) 36. а) в) 37. а) в) 38. в) 39. а) г) 40. а) в) 41-50. Найти наибольшее и наименьшее значения функции 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51-60. Найти неопределенные интегралы, результаты проверить дифференцированием. 51. а) 52. а) 53. а) 54. а) 55. а) 56. а) 57. а) 58. а) 59. а) 60. а) 61-70. 61. Дана функция 62.Дана функция 63. Дана функция 64. Дана функция 65. Дана функция 66. Дана функция 67. Дана функция 68. Дана функция 69. Дана функция 70. Дана функция
71-80. Найти частное решение дифференциального уравнения 71. 72. 73. 74. 75. 76. 77. 78. 79. 80. 81-90. Исследовать сходимость числового ряда. 81. 83. 85. 87. 89. 91-100. Разложить данную функцию 91. 92. 93. 94. 95. 96. 97. 98. 99. 100. 101-110. Представить заданную функцию 101. 102. 103. 104. 105. 106. 107. 108. 109. 110.
111-120. Вычислить приближенное значение определенного интеграла 111. 113. 115. 117. 119. 121-130. Подбор эмпирических формул по данным временного ряда. По результатам торгов на фондовой бирже составлена таблица зависимости ликвидности (времени реализации) пакета акций компании от количества акций в нем. Требуется найти зависимость времени продажи t(мин) от величины пакета m(тыс. акций) в виде трех формул t=am+b, t=a/m+b, t=am2+bm+c. Вычислить среднеквадратичные уклонения и выбрать наиболее подходящую эмпирическую формулу. Построить графики эмпирических зависимостей вместе с точками исходной таблицы. i – номер задания m (тыс.) – количество акций в пакете t (мин.) – время продажи пакета
Порядок выполнения задания: 1.Перейти с помощью преобразований от заданной нелинейной зависимости к линейной. Используя исходную таблицу с данными xi, yi составить для нее таблицу значений Xi, Yi для линейной зависимости. 2.Взять прямоугольную систему координат, подобрать масштаб, построить точки (Xi, Yi) из таблицы линейной зависимости. 3.Проверить правильность выбора эмпирической формулы: точки (Xi, Yi) должны располагаться примерно вдоль некоторой прямой. 4.Найти методом наименьших квадратов коэффициенты в линейной зависимости, перейти к коэффициентам нелинейной эмпирической формулы и записать эту формулу для исходной таблицы в виде функции y=f(x). 5.Найти уклонения эмпирической зависимости от значений исходной таблицы εi=f(xi)-yi, i=1, 2, …, n. 6.Вычислить среднеквадратичное уклонение 7. Построить график эмпирической формулы и на этом же чертеже нанести точки (Xi, Yi) исходной таблицы. 131-140. 131. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса; б) студент знает только два вопроса своего экзаменационного билета; в) студент знает только один вопрос своего экзаменационного билета. 132. В каждой из двух урн находится 5 белых и 10 чёрных шаров. Из первой урны во вторую переложили наудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что шар, вынутый из второй урны окажется чёрным. 133. Три стрелка в одинаковых и независимых условиях произвели по одному выстрелу по одной и той же цели. Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попадёт в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель. 134. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,7. Найти вероятность того, что в 1600 испытаниях событие наступит 900 раз. 135. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равно 0,9, второе – 0,95 и третье – 0,85. Найти вероятность того, что при аварии сработает: а) только одно устройство; б) только два устройства; в) все три устройства. 136. Верояность наступления события в каждом из одинаковых независимых испытаний равна 0,07. Найти вероятность того, что в 1400 испытаниях событие наступит 28 раз. 137. В партии из 1000 изделий имеется 10 дефектных. Найти вероятность того, что среди наудачу взятых из этой партии 50 изделий ровно 5 окажется дефектными. 138. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 225 испытаниях событие наступит не менее 75 и не больше 90 раз. 139. На трёх станках при одинаковых и независимых условиях изготавливаются детали одного наименования. На первом станке изготавливается10%, на втором – 30%, на третьем – 60% деталей. Для каждой детали вероятность быть бездефектной равна 0,7, если она изготовлена на первом станке; 0,8, если она изготовлена на втором станке; 0,9 – если она изготовлена на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.
140. Два брата входят в состав двух различных спортивных команд, состоящих из 12 человек каждая. В двух урнах имеется по12 билетов с номерами от 1 до 12. Члены каждой команды вынимают наудачу по одному билету из определённой урны (без возвращения). Найти вероятность того, что оба брата вытащат номер 6. 141-150. Дискретная случайная величина x может принимать только два значения x1 и x2, причём 141. p1=0.1 M(X)=3.9 D(X)=0.09 142. p1=0.3 M(X)=3.7 D(X)=0.21 143. p1=0.5 M(X)=3.5 D(X)=0.25 144. p1=0.7 M(X)=3.3 D(X)=0.21 145. p1=0.9 M(X)=3.1 D(X)=0.09 146. p1=0.9 M(X)=2.2 D(X)=0.36 147. p1=0.8 M(X)=3.2 D(X)=0.16 148. p1=0.8 M(X)=3.4 D(X)=0.24 149. p1=0.8 M(X)=3.6 D(X)=0.24 150. p1=0.8 M(X)=3.8 D(X)=0.16 151-160. Случайная величина Х задана функцией распределения (интегральной функцией) F(x). Найти плотность вероятности (дифференциальную функцию), математическое ожидание и дисперсию. Построить графики интегральной и дифференциальной функций. 151. 152. 153. 154. 155. 156. 157. 158. 159. 160. 161-170. Найти доверительный интервал для оценки математического ожидания a нормального распределения с надёжностью 0,96, зная выборочную среднюю 161. 162. 163. 164. 165. 166. 167. 168. 169. 170.
литература
|

 ,
,  ,
, 


 в некотором базисе. Доказать что векторы
в некотором базисе. Доказать что векторы 

 образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора  в этом базисе.
в этом базисе. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  ,
, ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
, 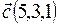 ,
,  .
. ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  ,
, ,
,  ,
,  ,
,  .
.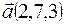 ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
. . Доказать ее совместность и решить тремя способами: 1) методом Гаусса; 2) средствами матричного исчисления; 3) по правилу Крамера.
. Доказать ее совместность и решить тремя способами: 1) методом Гаусса; 2) средствами матричного исчисления; 3) по правилу Крамера. 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 преобразованием графика функции
преобразованием графика функции  .
. 22.
22. 
 24.
24. 

 преобразованием графика функции
преобразованием графика функции  .
. 27.
27. 
 29.
29. 
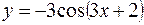
 данных функций.
данных функций. ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д) 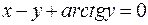 .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
. ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
.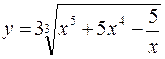 ; б)
; б) 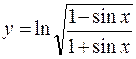 ;
; ; г)
; г)  ; д)
; д) 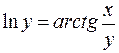 .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б)  ;
; ; г)
; г)  ; д)
; д)  .
. на отрезке
на отрезке  .
.
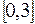

















 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. . Проверить, что:
. Проверить, что:  .
. . Проверить, что:
. Проверить, что:  .
.  . Проверить, что:
. Проверить, что:  .
. . Проверить, что:
. Проверить, что:  .
. . Проверить, что:
. Проверить, что:  .
. . Проверить, что:
. Проверить, что:  . Проверить, что:
. Проверить, что:  .
. . Проверить, что:
. Проверить, что:  . Проверить, что:
. Проверить, что:  .
. . Проверить, что:
. Проверить, что:  .
. , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  ,
,  .
. ;
;  ,
,  .
. ;
;  ,
,  .
.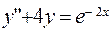 ;
;  ;
;  ,
,  .
. ;
;  .
. ;
;  ;
;  ;
;  ,
, 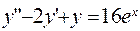 ;
;  .
. ;
;  ,
,  . 82.
. 82.  .
. . 84.
. 84.  .
. . 86.
. 86.  .
. . 88.
. 88.  .
. . 90.
. 90.  .
. в ряд Фурье в интервале (a; b).
в ряд Фурье в интервале (a; b). в интервале (-π; π).
в интервале (-π; π). в интервале (-2; 2).
в интервале (-2; 2). в интервале (-π; π).
в интервале (-π; π). в интервале (-1; 1).
в интервале (-1; 1).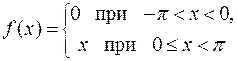 в интервале (-π; π).
в интервале (-π; π). в интервале (-2; 2).
в интервале (-2; 2). в интервале (-π; π).
в интервале (-π; π). в интервале (-1; 1).
в интервале (-1; 1). в интервале (0; 2π).
в интервале (0; 2π). в интервале (-π; π).
в интервале (-π; π). , где
, где  , в виде
, в виде  ; проверить, будет ли она аналитической, и в случае положительного ответа найти значение ее производной в заданной точке z 0.
; проверить, будет ли она аналитической, и в случае положительного ответа найти значение ее производной в заданной точке z 0. , z 0= -1+i.
, z 0= -1+i. , z 0=-i.
, z 0=-i. , z 0=1.
, z 0=1. , z 0=
, z 0=  i.
i. , z 0= -i.
, z 0= -i. , z 0=
, z 0=  .
. , z 0= 1-i.
, z 0= 1-i. , z 0=
, z 0=  i.
i. , z 0=
, z 0=  i.
i. , z 0= -1+iπ.
, z 0= -1+iπ. с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака. . 112.
. 112.  .
. . 114.
. 114.  .
. . 116.
. 116.  .
. . 118.
. 118.  .
. . 120.
. 120.  .
. .
. . Известны вероятность p1 возможного значения x1, математическое ожидание M(X) и дисперсия D(X). Найти закон распределения этой случайной величины.
. Известны вероятность p1 возможного значения x1, математическое ожидание M(X) и дисперсия D(X). Найти закон распределения этой случайной величины.









 . Объем выборки n и среднее квадратическое отклонение σ.
. Объем выборки n и среднее квадратическое отклонение σ. 75.17 n=36 σ =6
75.17 n=36 σ =6


