ОСНОВЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
§1. Понятие о преобразовании Лапласа. Оригинал и изображение
Пусть  – действительная функция действительного аргумента
– действительная функция действительного аргумента 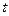 , определенная при любых
, определенная при любых 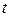 .
.
Определение. Будем называть оригиналом функцию  , если она удовлетворяет следующим условиям:
, если она удовлетворяет следующим условиям:
1)  – кусочно-непрерывная функция при
– кусочно-непрерывная функция при  ; это значит, что она или непрерывна, или имеет точки разрыва первого рода, число которых конечно на любом конечном интервале;
; это значит, что она или непрерывна, или имеет точки разрыва первого рода, число которых конечно на любом конечном интервале;
2)  при
при  ;
;
3)  с возрастанием
с возрастанием 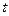 может возрастать, но не быстрее некоторой показательной функции. Это означает, что существуют такие числа
может возрастать, но не быстрее некоторой показательной функции. Это означает, что существуют такие числа  и
и  что для всех
что для всех 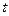 выполняется
выполняется  , число
, число  называется показателем роста функции
называется показателем роста функции  . (Для ограниченных функций можно принять
. (Для ограниченных функций можно принять  ).
).
В связи с условием 2 в дальнейшем изложении, где это потребуется, будем записывать для краткости лишь то выражение  , которое она имеет для
, которое она имеет для  , подразумевая, что для
, подразумевая, что для  . Например, запись
. Например, запись  должна пониматься так:
должна пониматься так: 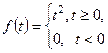 .
.
Определение. Изображением функции  – оригинала – называется функция
– оригинала – называется функция  комплексного переменного
комплексного переменного  , определяемая интегралом
, определяемая интегралом
 . (1)
. (1)
Несобственный интеграл в правой части равенства (1), называемый интегралом Лапласа, зависит от параметра  .
.
Соотношение (1) осуществляет преобразование одной функции в другую. Операцию перехода от оригинала  к изображению
к изображению  в соответствии с формулой (1) называют преобразованием Лапласа, или прямым преобразованием Лапласа.
в соответствии с формулой (1) называют преобразованием Лапласа, или прямым преобразованием Лапласа.
Тот факт, что  есть изображение (говорят также, изображение по Лапласу), символически записывают так:
есть изображение (говорят также, изображение по Лапласу), символически записывают так:
 .
.
Отыскание оригинала  по изображению
по изображению  называют
называют  обращением преобразования Лапласа, или обратным преобразованием Лапласа; его обозначают символом
обращением преобразования Лапласа, или обратным преобразованием Лапласа; его обозначают символом  .
.
Условились обозначать оригиналы малыми буквами  а их изображения – соответствующими заглавными буквами
а их изображения – соответствующими заглавными буквами  или теми же буквами, что и оригиналы, но снабжать их черточками сверху:
или теми же буквами, что и оригиналы, но снабжать их черточками сверху:  .
.
§2. Теоремы существования изображения и единственности оригинала
Теорема (существования изображения). Если функция  является оригиналом, то ее изображение
является оригиналом, то ее изображение 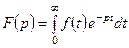 определено для всех значений комплексного переменного
определено для всех значений комплексного переменного  , удовлетворяющих условию
, удовлетворяющих условию  , т.е. в полуплоскости
, т.е. в полуплоскости  , где
, где  – показатель роста функции
– показатель роста функции  , и является аналитической функцией в этой области.
, и является аналитической функцией в этой области.
Геометрически теорему можно истолковать так: если на комплексной плоскости  через точку
через точку  действительной оси
действительной оси  провести прямую параллельно мнимой оси
провести прямую параллельно мнимой оси  , то интеграл (1) сходится везде в области, расположенной правее от этой прямой, причем функция
, то интеграл (1) сходится везде в области, расположенной правее от этой прямой, причем функция  является аналитической в ней.
является аналитической в ней.
Следствие (поведение изображения на бесконечности). Если точка
р стремится в бесконечность так, что

, то изображение

.
Теорема существования устанавливает условия, при которых функции  действительного переменного ставится в соответствие единственная функция
действительного переменного ставится в соответствие единственная функция  комплексного переменного – ее изображение.
комплексного переменного – ее изображение.
Теорема (единственности оригинала). Если  является изображением двух оригиналов
является изображением двух оригиналов  и
и  , то эти оригиналы совпадают во всех точках, в которых они непрерывны.
, то эти оригиналы совпадают во всех точках, в которых они непрерывны.
Различные разрывные функции могут иметь одинаковое изображение.
§3. Свойства преобразования Лапласа
Теорема линейности
Для любых действительных или комплексных чисел С и С 2
 (4)
(4)
т.е. линейной комбинации оригиналов соответствует такая же линейная комбинация изображений.
Теорема линейности справедлива для любого конечного числа слагаемых:

В частности, при  имеем
имеем 
Теорема подобия
Если  то для любого числа
то для любого числа 
 (5)
(5)
т.е. умножение аргумента оригинала на положительное число  приводит к делению аргумента изображения и самого изображения
приводит к делению аргумента изображения и самого изображения  на это число.
на это число.
Теорема смещения
Если  , то для любого числа
, то для любого числа  – действительного или комплексного
– действительного или комплексного 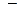 имеет место соотношение
имеет место соотношение
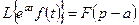 при
при  , (6)
, (6)
т.е. умножение оригинала на функцию  влечет за собой «смещение» аргумента изображения на
влечет за собой «смещение» аргумента изображения на  .
.
Теорема запаздывания
Если  , то для любого числа
, то для любого числа  имеет место
имеет место
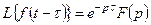 , (7)
, (7)
т.е. запаздывание аргумента оригинала на положительную величину  приводит к умножению изображения оригинала без запаздывания на
приводит к умножению изображения оригинала без запаздывания на  .
.
Теорема дифференцирования оригинала
Если  непрерывно дифференцируема и
непрерывно дифференцируема и  является оригиналом, то из
является оригиналом, то из  следует:
следует:
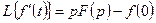 , (8)
, (8)
т.е. дифференцирование оригинала сводится к умножению его изображения на параметр  и вычитанию
и вычитанию  , где под
, где под  следует понимать
следует понимать  .
.
 . (9)
. (9)
§4. Обратное преобразование Лапласа
Теорема обращения
Если функция  – оригинал, а
– оригинал, а  ее изображение, то в любой точке
ее изображение, то в любой точке 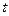 непрерывности функции
непрерывности функции  имеет место формула обращения
имеет место формула обращения
 (10)
(10)
где 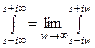 и
и  – любое действительное число больше показателя роста
– любое действительное число больше показателя роста  .
.
Комплексный интеграл в (10), осуществляющий обратное преобразование Лапласа, вычисляется вдоль любой вертикальной прямой  лежащей в полуплоскости
лежащей в полуплоскости  сходимости интеграла Лапласа от функции
сходимости интеграла Лапласа от функции  .
.
Соотношение (10), называемое формулой Римана-Меллина, решает в общем случае задачу отыскания оригинала  по заданному его изображению
по заданному его изображению 
В простейших случаях при нахождении оригинала можно не прибегать к формуле обращения (10), а пользоваться таблицей соответствий между оригиналами и изображениями и основными свойствами преобразования Лапласа.
Пример. Найти оригиналы по данным изображениям;
а)  , б)
, б)  .
.
Решение. а) представим  в виде
в виде
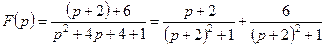 .
.
Используя свойство линейности и соответствия (10), (9) из таблицы оригиналов и их изображений, найдем
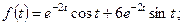
б) заметим, что  Согласно свойству линейности и соответствиям (1), (2) из таблицы получим, что
Согласно свойству линейности и соответствиям (1), (2) из таблицы получим, что  . Тогда для заданного изображения
. Тогда для заданного изображения  оригинал может быть найден с помощью теоремы запаздывания. Полагая
оригинал может быть найден с помощью теоремы запаздывания. Полагая 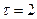 , получим
, получим
 .●
.●
Если изображение  представляет собой правильную рациональную дробь
представляет собой правильную рациональную дробь  , где
, где  и
и  – многочлены от
– многочлены от  , причем степень числителя меньше степени знаменателя, то при нахождении оригинала поступают следующим образом: разлагают дробь на сумму простейших дробей вида
, причем степень числителя меньше степени знаменателя, то при нахождении оригинала поступают следующим образом: разлагают дробь на сумму простейших дробей вида

находят оригинал для каждого слагаемого и, суммируя, получают оригинал данной функции.
Литература
1. Бугров, Я. С. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного: Учеб. для вузов / Я. С. Бугров, С. М. Никольский. – М.: Наука, 1981. – 448 с. – С.420-443.
2. Данко П. Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2: Учеб. пособие для вузов / П. Е. Данко. – 6-е изд., испр. – М.: ООО «Издательство Оникс»; ООО «Издательство «Мир и образование», 2007. – 416 с. – С.305-320.
 , то изображение
, то изображение  .
.

 – действительная функция действительного аргумента
– действительная функция действительного аргумента  , определенная при любых
, определенная при любых 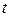 .
. ; это значит, что она или непрерывна, или имеет точки разрыва первого рода, число которых конечно на любом конечном интервале;
; это значит, что она или непрерывна, или имеет точки разрыва первого рода, число которых конечно на любом конечном интервале; при
при  ;
; и
и  что для всех
что для всех  , число
, число  называется показателем роста функции
называется показателем роста функции  ).
). . Например, запись
. Например, запись  должна пониматься так:
должна пониматься так: 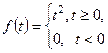 .
. комплексного переменного
комплексного переменного  , определяемая интегралом
, определяемая интегралом . (1)
. (1) .
. .
. называют
называют  обращением преобразования Лапласа, или обратным преобразованием Лапласа; его обозначают символом
обращением преобразования Лапласа, или обратным преобразованием Лапласа; его обозначают символом  .
. а их изображения – соответствующими заглавными буквами
а их изображения – соответствующими заглавными буквами  или теми же буквами, что и оригиналы, но снабжать их черточками сверху:
или теми же буквами, что и оригиналы, но снабжать их черточками сверху:  .
.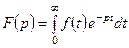 определено для всех значений комплексного переменного
определено для всех значений комплексного переменного  , т.е. в полуплоскости
, т.е. в полуплоскости  , где
, где  провести прямую параллельно мнимой оси
провести прямую параллельно мнимой оси  , то интеграл (1) сходится везде в области, расположенной правее от этой прямой, причем функция
, то интеграл (1) сходится везде в области, расположенной правее от этой прямой, причем функция 
 и
и  , то эти оригиналы совпадают во всех точках, в которых они непрерывны.
, то эти оригиналы совпадают во всех точках, в которых они непрерывны. (4)
(4)
 имеем
имеем 
 то для любого числа
то для любого числа 
 (5)
(5) приводит к делению аргумента изображения и самого изображения
приводит к делению аргумента изображения и самого изображения  , то для любого числа
, то для любого числа  имеет место соотношение
имеет место соотношение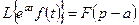 при
при  , (6)
, (6) влечет за собой «смещение» аргумента изображения на
влечет за собой «смещение» аргумента изображения на  , то для любого числа
, то для любого числа  имеет место
имеет место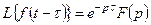 , (7)
, (7) приводит к умножению изображения оригинала без запаздывания на
приводит к умножению изображения оригинала без запаздывания на  .
. является оригиналом, то из
является оригиналом, то из 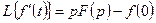 , (8)
, (8) , где под
, где под  .
. . (9)
. (9) – оригинал, а
– оригинал, а  имеет место формула обращения
имеет место формула обращения (10)
(10)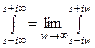 и
и  лежащей в полуплоскости
лежащей в полуплоскости  сходимости интеграла Лапласа от функции
сходимости интеграла Лапласа от функции 
 , б)
, б)  .
.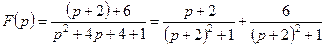 .
.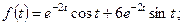
 Согласно свойству линейности и соответствиям (1), (2) из таблицы получим, что
Согласно свойству линейности и соответствиям (1), (2) из таблицы получим, что  . Тогда для заданного изображения
. Тогда для заданного изображения 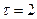 , получим
, получим .●
.● , где
, где  и
и  – многочлены от
– многочлены от 



