Лабораторная работа №3. Алгоритм Дейкстри знаходить найкоротшу відстань від однієї вершини до всіх інших

Алгоритм Дейкстри знаходить найкоротшу відстань від однієї вершини до всіх інших. Всі ваги ребер повинні бути додатними числами.

Кожній вершині графа ставиться у відповідність мітка mark, що містить мінімальну відстань від першої вершини до поточної вершини, мінімальний шлях від першої до поточної вершини зберігається в масиві L. На початку всі мітки дорівнюють ∞. Алгоритм полягає у тому, що на кожному кроці перебираються всі можливі варіанти просування по графу. При знаходженні більш короткого шляху від вершини V₁ до вершини V₂, значення мітки вершини V₂ замінюється на довжину цього шляху, і так доти, поки не буде пройдено весь граф. Вкінці роботи програми у масиві L будуть міститися найкоротші шляхи від першої вершини до всіх інших вершин.

Приклад 2. Розглянемо прикладну задачу, для рішення якої необхідно знайти найкоротшу відстань у графі між двома вершинами.

	A	B	C	D	E
A
B
C
D
E

Логістичний відділ служби доставки X хоче визначити, яким шляхом швидше доставити посилки з міста А в місто Е. Проаналізувавши карту доріг країни, спеціалісти логістичного відділу побудували граф, зображений на рис. 18.

 

 

		в)
	а)

 

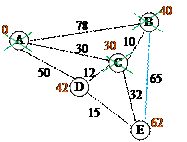
Рисунок 18 – а) граф, вершини якого міста, ребра – дороги між ними, а ваги ребер – довжини доріг; в) матриця суміжності наведеного графу

1 Крок. Привласнюємо кожній вершині мітку. Першій – 0, іншим ­– ∞. Створюємо масив L, в який будемо записувати шляхи від А до інших вершин та масив Mark для значення міток і інформації про закреслені мітки.

L =	A	B	C	D	E
A

Mark =	A	B	C	D	E
	∞	∞	∞	∞

 

Рисунок 19

2 Крок. Присвоїмо міткам вершин, що знаходяться на відстані одного переходу від вершини А, довжини цих переходів, якщо вони менші за поточні значення мітки. Вкажемо нові маршрути та закреслимо вершину А.

L =	A	B	C	D	E
A	A	A	A

Mark =	A	B	C	D	E
				∞

 

 

Рисунок 20

 

3 Крок. Виберемо незакреслену вершину з найменшою міткою. Зараз це вершина С. Присвоїмо міткам вершин, що знаходяться на відстані одного переходу від вершини С, довжини цих переходів + значення мітки С, якщо ці значення менші за поточні значення відповідних міток. Вкажемо нові маршрути та закреслимо вершину С.

L =	A	B	C	D	E
A	С	A	С	С

Mark =	A	B	C	D	E

 

 

Рисунок 21

 

4 Крок. Виберемо незакреслену вершину з найменшою міткою. Зараз це вершина В. Присвоїмо міткам вершин, що знаходяться на відстані одного переходу від вершини В, довжини цих переходів + значення мітки В, якщо ці значення менші за поточні значення відповідних міток. Нових маршрутів немає. Закреслимо вершину В.

L =	A	B	C	D	E
A	С	A	С	С

Mark =	A	B	C	D	E

 

 

Рисунок 22

 

5 Крок. Виберемо незакреслену вершину з найменшою міткою. Зараз це вершина D. Присвоїмо міткам вершин, що знаходяться на відстані одного переходу від вершини D, довжини цих переходів + значення мітки D, якщо ці значення менші за поточні значення відповідних міток. Вкажемо нові маршрути та закреслимо вершину D.

L =	A	B	C	D	E
A	С	A	С	D

Mark =	A	B	C	D	E

 

 

Рисунок 23

 

Результат:Матриця Lвказує в яке місто через яке їхати. З неї можна у зворотному порядку прослідкувати найкоротший маршрут з будь-якого міста до міста А. Найкоротший шлях від міста Е до міста А лежить через міста D та С. Отже, значення необхідного маршруту: A ® C ® D ® Е.

 

Завдання до лабораторної роботи:

Реалізувати програмно абстрактний тип даних неорієнтований граф. Створити його екземпляр, який заповнити даними, вказаними у Вашому варіанті. Розробити програму, що повинна:

1. Побудувати для даного графу мінімальне каркасне дерево, використовуючи алгоритм Прима-Крускала, визначити сумарну вагу побудованого дерева, вивести одержані дані на екран.

2. Визначити та вивести на екран найкоротший шлях від вершини 1 до вершини 6 за допомогою алгоритму Дейкстри.

 

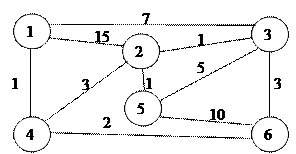
Варіант 1

 

 

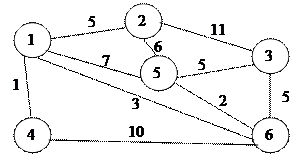
Варіант 2

 

 

Варіант 3

 

 

Варіант 4

 

 

Варіант 5

 

 

Варіант 6

 

Варіант 7

 

 

Варіант 8

 

 

Варіант 9

 

Варіант 10

 

 

Варіант 11

 

 

Варіант 12

 

 

Варіант 13

 

 

Варіант 14

 

Варіант 15

 

Лабораторная работа №3