Используем t-критерий Стьюдента.
а) Выдвинем нулевую гипотезу, о том, что коэффициент регрессии b равен нулю, т.е. H0: b = 0, и фактор x не оказывает влияния на результат. Вычислим
По таблице найдем Поскольку б) Выдвинем нулевую гипотезу, о том, что коэффициент регрессии а равен нулю, т.е. H0: а = 0. Вычислим
Поскольку 2. Доверительные интервалы:
Поскольку в доверительный интервал для коэффициента b не попал 0, а в интервал для коэффициента а попал, то коэффициент b признается статистически значимым, а коэффициент а – статистически не значимым.
4) Оценим статистическую значимость уравнения регрессии в целом, используя: а) Дисперсионный анализ. Построим вспомогательную таблицу:
Обозначим SSобщ = где Тогда: SSобщ = 213,6; SSA = 193,885 и SSR = 19,715 Найдем средний квадрат отклонений или дисперсию на одну степень свободы:
Вычислим Критическая точка критерия Fкр=F(α; 1; n-2) )=F( 0,05; 1; 8 ) = 5,32 Поскольку
б) Используем элементы теории корреляции. Найдем линейный коэффициент корреляции по формуле:
Значение Найдем коэффициент детерминации R2: R2 = rxy2 R2 = 0,9077, это говорит о том, что вариация результата y на 90,77% объясняется вариацией переменной x, и поскольку это значение близко к 1, то признаётся статистическая значимость уравнения регрессии в целом.
|

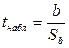
 = 8,8699.
= 8,8699.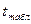 = t(α; n-2) = t( 0,05; 8 ) = 2,306.
= t(α; n-2) = t( 0,05; 8 ) = 2,306.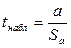
 <
<  )2
)2
 –
–  , SSА =
, SSА =  и SSR =
и SSR = 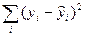 ,
, ,
,  = a + bxi.
= a + bxi. = 19,715;
= 19,715;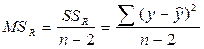 = 2,4644.
= 2,4644. = 78,675
= 78,675 > Fкр, то гипотеза Н0: b=0 отвергается, признаётся статистическая значимость уравнения регрессии, т.е. связь между рассматриваемыми признаками есть и результаты наблюдений не противоречат предположению о её линейности.
> Fкр, то гипотеза Н0: b=0 отвергается, признаётся статистическая значимость уравнения регрессии, т.е. связь между рассматриваемыми признаками есть и результаты наблюдений не противоречат предположению о её линейности.
 = 0,9527
= 0,9527


