Задание. Модель парной линейной регрессии.
Данные наблюдений представлены в таблице:
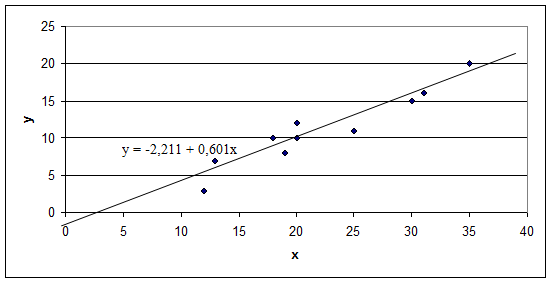
2) Построим уравнение линейной регрессии: yi=α+βxi+εi Составим вспомогательную таблицу:
Найдем оценки неизвестных параметров с помощью метода наименьших квадратов, получим:
Уравнение регрессии будет: y = -2,211 + 0,606x
Построим доверительные интервалы для параметров модели. Формулы для расчета доверительных интервалов имеют следующий вид:
которые с надёжностью 95% накрывают определяемые параметры α и β. Для их нахождения построим вспомогательную расчетную таблицу:
Найдем стандартные ошибки коэффициентов регрессии:
где Тогда: S = 1,570
По таблице значений критерия Стьюдента находим
3) Оценим статистическую значимость коэффициентов регрессии а и b:
|
,
,
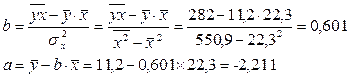
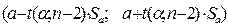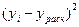
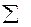
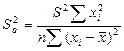
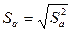- стандартная ошибка коэффициента регрессии a.
- стандартная ошибка коэффициента регрессии b,
, 
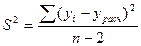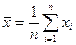
= 1,591
0,068
, тогда, подставляя в формулы интервалов известные данные, получим доверительные интервалы:
