Цель и задачи практики
2.1. Нормировочный множитель Ψ-функции [1 балл] 1) ψ-Функция некоторой частицы имеет вид 2) Используя условие нормировки вероятностей, определить нормировочный коэффициент A волновой функции 3) ψ-Функция некоторой частицы имеет вид 4) ψ-Функция некоторой частицы имеет вид 5) ψ-Функция некоторой частицы имеет вид 6) ψ-Функция некоторой частицы имеет вид 7) ψ-Функция некоторой частицы имеет вид 8) ψ-Функция некоторой частицы имеет вид 9) ψ-Функция некоторой частицы имеет вид 10) ψ-Функция некоторой частицы имеет вид 11) ψ-Функция некоторой частицы имеет вид 12) Используя условие нормировки вероятностей, определить нормировочный коэффициент A волновой функции 13) ψ-Функция некоторой частицы имеет вид 14) ψ-Функция некоторой частицы имеет вид 15) Волновая функция
2.2. Вероятность и средние значения параметров [2 балла] 1) ψ-Функция некоторой частицы имеет вид 2) Частица в одномерной прямоугольной «потенциальной яме» шириной ℓ; с бесконечно высокими «стенками» находится в основном состоянии. Определить вероятность обнаружения частицы в левой трети «ямы». [2 балла] Ответ: 0,195 3) Частица в одномерной прямоугольной «потенциальной яме» шириной ℓ; с бесконечно высокими «стенками» находится в возбужденном состоянии (n = 2). Определить вероятность обнаружения частицы в области 4) Волновая функция, описывающая некоторую частицу, имеет вид 5) Электрон находится в одномерной прямоугольной «потенциальной яме» шириной ℓ; с бесконечно высокими «стенками». Определить вероятность обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n = 3). [2 балла] Ответ: 0,33 6) В одномерном «потенциальном ящике» шириной ℓ; находится электрон. Вычислить вероятность нахождения электрона на первом энергетическом уровне в интервале ¼ ℓ;, равноудаленном от стенок «ящика». [2 балла] Ответ: 0,475 7) Волновая функция, описывающая основное состояние электрона в атоме водорода, имеет вид 8) Электрон находится в одномерной прямоугольной «потенциальной яме» шириной ℓ; с бесконечно высокими «стенками». Определить вероятность обнаружения электрона в средней трети «ямы», если электрон находится в возбужденном состоянии (n = 2). [2 балла] Ответ: 0,195 9) В одномерном «потенциальном ящике» шириной ℓ; находится электрон. Вычислить вероятность нахождения электрона на низшем возбужденном энергетическом уровне в интервале ¼ ℓ;, равноудаленном от стенок «ящика». [2 балла] Ответ: 0,091 10) Вычислить отношение вероятностей W1/W2 нахождения электрона на первом и втором энергетических уровнях в интервале ¼ ℓ;, равноудаленном от стенок одномерной «потенциальной ямы» шириной ℓ;. [2 балла] Ответ: 5,22 11) Волновая функция, описывающая некоторую частицу, имеет вид 12) Частица в одномерной прямоугольной «потенциальной яме» шириной ℓ; с бесконечно высокими «стенками» находится в основном состоянии. Определить вероятность обнаружения частицы в средней трети «ямы». [2 балла] Ответ: 0,609 13) В одномерном «потенциальном ящике» шириной ℓ; находится электрон. Вычислить вероятность нахождения электрона на низшем возбужденном энергетическом уровне в интервале от 0 до ¼ ℓ;. [2 балла] Ответ: 0,25 14) Электрон находится в одномерном «потенциальном ящике» шириной ℓ;=10 нм. Определить среднее значение координаты ‹x› электрона (0<x< ℓ;) [2 балла] Ответ: 5 нм 15) В одномерной «потенциальной яме» шириной ℓ; находится электрон в возбужденном состоянии (n =4). Вычислить вероятность нахождения электрона в первой четверти «ямы». [2 балла] Ответ: 0,25
2.3. Одномерная прямоугольная яма [1 балл] 1) Частица находится в потенциальном ящике. Найти отношение разности соседних энергетических уровней D En +1, n к энергии Еn частицы в случае n = 5. [1 балл] Ответ: 2) Электрон находится в потенциальном ящике. Определить ширину l потенциальной ямы, если разность D E 5,4 между пятым и четвертым энергетическими уровнями электрона составляет 2 эВ. [1 балл] Ответ: 3) Частица находится в потенциальном ящике. Найти отношение разности соседних энергетических уровней D En +1, n к энергии Еn частицы в случае п → ∞. [1 балл] Ответ: 4) Частица в потенциальном ящике шириной l находится в возбужденном состоянии (n = 2). Определить, в каких точках интервала (0< x < l) плотность вероятности ω нахождения частицы максимальна. Ответ выразить в долях l. [1 балл] Ответ: x = 0,25 и 0,75. 5) Электрон находится в потенциальном ящике шириной l = 0,6 нм. Определить разность D E 3,2 между третьим и вторым энергетическими уровнями электрона. Ответ выразить в электрон-вольтах. [1 балл] Ответ: 6) Электрон находится в потенциальном ящике шириной l = 1 нм в возбужденном состоянии (n = 3). Вычислить плотность вероятности ω в центре ящика. [1 балл] Ответ: 7) Электрон находится в потенциальном ящике шириной l = 0,5 нм. Определить наименьшую разность D E энергетических уровней электрона. Ответ выразить в электрон-вольтах. [1 балл] Ответ: 8) Электрон находится в потенциальном ящике шириной l = 0,4 нм в возбужденном состоянии (n = 4). Вычислить плотность вероятности ω в центре ящика. [1 балл] Ответ: 9) Частица находится в потенциальном ящике. Найти отношение разности соседних энергетических уровней D En +1, n к энергии Еn частицы в случае n = 13. [1 балл] Ответ: 10) Электрон находится в потенциальном ящике. Определить ширину l потенциальной ямы, если разность D E 6,5 между шестым и пятым энергетическими уровнями электрона составляет 1 эВ. [1 балл] Ответ: 11) Частица в потенциальном ящике шириной l находится в возбужденном состоянии (n = 2). Определить, в каких точках интервала (0< x < l) плотность вероятности ω нахождения частицы минимальна. Ответ выразить в долях l. [1 балл] Ответ: x = 0,5. 12) Электрон находится в потенциальном ящике шириной l = 0,3 нм. Определить разность D E 3,2 между четвертым и третьим энергетическими уровнями электрона. Ответ выразить в электрон-вольтах. [1 балл] Ответ: 13) Электрон находится в потенциальном ящике шириной l = 1 нм в возбужденном состоянии (n = 4). Вычислить плотность вероятности ω в точке x = 14) Электрон находится в потенциальном ящике шириной l = 1,5 нм. Определить наименьшую разность D E энергетических уровней электрона. Ответ выразить в электрон-вольтах. [1 балл] Ответ: 15) Электрон находится в потенциальном ящике шириной l = 0,8 нм в возбужденном состоянии (n = 5). Вычислить плотность вероятности ω в точке x =
2.4. Многомерная яма [3 балла] 1) Электрон находится в двумерной прямоугольной потенциальной яме размерами 0,5×0,5 нм с абсолютно непроницаемыми стенками. Найти энергию первого вырожденного уровня в эВ. [3 балла] Ответ: 2) Электрон находится в двумерной прямоугольной потенциальной яме размерами 0,3×0,3 нм с абсолютно непроницаемыми стенками. Какую энергию в эВ должен получить электрон, чтобы перейти с первого уровня на третий. [3 балла] Ответ: 3) Электрон находится в двумерной прямоугольной потенциальной яме размерами 0,2×0,4 нм с абсолютно непроницаемыми стенками на третьем энергетическом уровне. Найти плотность вероятности w нахождения электрона в точке с координатами (0,15 нм; 0,05 нм). [3 балла] Ответ: 4) Электрон находится в двумерной прямоугольной потенциальной яме размерами 0,3×0,6 нм с абсолютно непроницаемыми стенками. Найти энергию четвертого уровня в эВ. [3 балла] Ответ: 5) Электрон находится в двумерной прямоугольной потенциальной яме размерами 1×1 нм с абсолютно непроницаемыми стенками. Какую энергию в эВ должен получить электрон, чтобы перейти с первого уровня на третий. [3 балла] Ответ: 6) Электрон находится в двумерной прямоугольной потенциальной яме размерами 1×2 нм с абсолютно непроницаемыми стенками на втором энергетическом уровне. Найти плотность вероятности w нахождения электрона в точке с координатами (0,25 нм; 0,5 нм). [3 балла] Ответ: 7) Электрон находится в двумерной прямоугольной потенциальной яме размерами 0,5×0,5 нм с абсолютно непроницаемыми стенками. Найти энергию второго вырожденного уровня в эВ. [3 балла] Ответ: 8) Электрон находится в двумерной прямоугольной потенциальной яме размерами 1×2 нм с абсолютно непроницаемыми стенками. Найти энергию четвертого уровня в эВ. [3 балла] Ответ: 9) Электрон находится в двумерной прямоугольной потенциальной яме размерами 1,2×1,2 нм с абсолютно непроницаемыми стенками на третьем энергетическом уровне. Найти плотность вероятности w нахождения электрона в точке с координатами (0,4 нм; 0,4 нм). [3 балла] Ответ: 10) Электрон находится в двумерной прямоугольной потенциальной яме размерами 1,5×1,5 нм с абсолютно непроницаемыми стенками. Найти энергию первого вырожденного уровня в эВ. [3 балла] Ответ: 11) Электрон находится в двумерной прямоугольной потенциальной яме размерами 1×2 нм с абсолютно непроницаемыми стенками. Какую энергию в эВ должен получить электрон, чтобы перейти с первого уровня на третий. [3 балла] Ответ: 12) Электрон находится в двумерной прямоугольной потенциальной яме размерами 0,6×0,6 нм с абсолютно непроницаемыми стенками на третьем энергетическом уровне. Найти плотность вероятности w нахождения электрона в точке с координатами (0,2 нм; 0,4 нм). [3 балла] Ответ: 13) Электрон находится в двумерной прямоугольной потенциальной яме размерами 0,4×0,8 нм с абсолютно непроницаемыми стенками. Какую энергию в эВ должен получить электрон, чтобы перейти с первого уровня на третий. [3 балла] Ответ: 14) Электрон находится в двумерной прямоугольной потенциальной яме размерами 1,5×1,5 нм с абсолютно непроницаемыми стенками. Найти энергию второго вырожденного уровня в эВ. [3 балла] Ответ: 15) Электрон находится в двумерной прямоугольной потенциальной яме размерами 1,2×0,6 нм с абсолютно непроницаемыми стенками на четвертом энергетическом уровне. Найти плотность вероятности w нахождения электрона в точке с координатами (0,4 нм; 0,4 нм). [3 балла] Ответ:
2.5. Барьер [2 балла] 1) Электрон обладает энергией E = 16 эВ. Определить, во сколько раз уменьшится его скорость n при прохождении через потенциальный барьер (см. рис.) высотой U = 12 эВ. [2 балла]
Ответ: 2) Электрон обладает энергией E = 18 эВ. Определить, во сколько раз увеличится его длина волны де Бройля l при прохождении через потенциальный барьер (см. рис.) высотой U = 16 эВ. [2 балла]
Ответ: 3) Определить коэффициент преломления n волн де Бройля для протонов на границе потенциальной ступени (см. рис.). Кинетическая энергия E протонов равна 10 эВ, а высота U потенциальной ступени равна 8 эВ. [2 балла]
Ответ: 4) Кинетическая энергия E электрона в три раза превышает высоту U потенциального барьера. Определить коэффициент отражения r электронов на границе барьера. [2 балла] Ответ: 5) Вычислить коэффициент прохождения t электрона с энергией E = 81 эВ через потенциальный барьер высотой U = 80,75 эВ. [2 балла] Ответ: 6) Коэффициент преломления n волн де Бройля для протонов на границе барьера равен 0,3. Определить коэффициент прохождения t. [2 балла] Ответ: 7) При какой ширине d прямоугольного потенциального барьера коэффициент прозрачности D для электронов равен 0,02? Разность энергий U – Е = 5 эВ. [2 балла] Ответ: 8) Протон и электрон прошли одинаковую ускоряющую разность потенциалов Dj = 20 кВ. Во сколько раз коэффициент прозрачности De для электрона больше коэффициента прозрачности Dp для протона, если высота U барьера равна 25 кэВ и ширина d = 0,l пм? [2 балла] Ответ: 9) Электрон обладает энергией E = 25 эВ. Определить, во сколько раз увеличится его скорость n при прохождении границы потенциальной ступени (см. рис.) высотой U = 9 эВ. [2 балла]
Ответ: 10) Электрон обладает энергией E = 9 эВ. Определить, во сколько раз уменьшится его длина волны де Бройля l при прохождении при прохождении границы потенциальной ступени (см. рис.) высотой U = 5 эВ. [2 балла]
Ответ: 11) Определить коэффициент преломления n волн де Бройля для протонов на границе потенциальной ступени (см. рис.). Кинетическая энергия E протонов равна 4 эВ, а высота U потенциальной ступени равна 3 эВ. [2 балла]
Ответ: 12) Кинетическая энергия E электрона в четыре раза превышает высоту U потенциального барьера. Определить коэффициент отражения r электронов на границе барьера. [2 балла] Ответ: 13) Вычислить коэффициент прохождения t электрона с энергией E = 50 эВ через потенциальный барьер высотой U = 49,2 эВ. [2 балла] Ответ: 14) Коэффициент преломления n волн де Бройля для протонов на границе барьера равен 0,25. Определить коэффициент прохождения t. [2 балла] Ответ: 15) Протон и электрон прошли одинаковую ускоряющую разность потенциалов Dj = 13,5 кВ. Во сколько раз коэффициент прозрачности De для электрона больше коэффициента прозрачности Dp для протона, если высота U барьера равна 15 кэВ и ширина d = 0,2 пм? [2 балла] Ответ:
Цель и задачи практики
Целью технологической практики является закрепление теоретических знаний, полученных в университете при изучении дисциплин «Архитектура», «Строительное материаловедение», подготовка к изучению дисциплин «Технология строительного производства», «Организация строительного производства». Задачами технологической практики являются: - изучение основных организационно-технологических решений строительного производства при возведении объекта; - изучение основных положений по инженерной подготовке строительной площадки; - изучение технологии и организации производственных процессов при выполнении основных видов строительно-монтажных работ; - приобретение практических навыков выполнения отдельных технологических операций строительных работ. Технологическая практика должна обеспечивать формирование следующих групп компетенций: академические, профессиональные. Академические компетенции должны включать в себя знания и умения по разделам дисциплин, которые представлены в программе практики. Профессиональные компетенции должны включать в себя знания и умения по технологии и организации строительно-монтажных работ, а также навыки выполнения отдельных технологических операций строительных работ.
|

 , где r – расстояние этой частицы до силового центра; a = 0,1 нм. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ
, где r – расстояние этой частицы до силового центра; a = 0,1 нм. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ  = 4·104 м–1/2
= 4·104 м–1/2 , описывающей основное состояние электрона в атоме водорода, где r – расстояние электрона от ядра; a = 53 пм (первый боровский радиус). [1 балл] Ответ
, описывающей основное состояние электрона в атоме водорода, где r – расстояние электрона от ядра; a = 53 пм (первый боровский радиус). [1 балл] Ответ 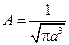 =1.46·1015 м-3/2
=1.46·1015 м-3/2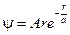 , где r – расстояние этой частицы до силового центра; a = 1 пм. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ
, где r – расстояние этой частицы до силового центра; a = 1 пм. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ  =3,26·1019 м-5/2
=3,26·1019 м-5/2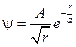 , где r – расстояние этой частицы до силового центра; a = 1 нм. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ
, где r – расстояние этой частицы до силового центра; a = 1 нм. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ  =5,64·108м-1
=5,64·108м-1 , где r – расстояние этой частицы до силового центра; a = 0,2 нм. Используя условие нормировки вероятностей, определить нормировочный коэффициент [1 балл] Ответ A.
, где r – расстояние этой частицы до силового центра; a = 0,2 нм. Используя условие нормировки вероятностей, определить нормировочный коэффициент [1 балл] Ответ A.  =1,15·1019 м-2
=1,15·1019 м-2 , где r – расстояние этой частицы до силового центра; a = 1010 м-1. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ
, где r – расстояние этой частицы до силового центра; a = 1010 м-1. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ  =4·104 м-1/2
=4·104 м-1/2 , где r – расстояние этой частицы до силового центра; a = 108 м-1. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ
, где r – расстояние этой частицы до силового центра; a = 108 м-1. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ  = 56,4·1010 м-3/2
= 56,4·1010 м-3/2 , где r – расстояние этой частицы до силового центра; a = 108 м-1 Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ
, где r – расстояние этой частицы до силового центра; a = 108 м-1 Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ  =3,26·1019 м-5/2
=3,26·1019 м-5/2 , где r – расстояние этой частицы до силового центра; a = 2·1010 м-1. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ
, где r – расстояние этой частицы до силового центра; a = 2·1010 м-1. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ  =1,84·1020 м-2
=1,84·1020 м-2 , где r – расстояние этой частицы до силового центра; a = 0,1 нм. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ
, где r – расстояние этой частицы до силового центра; a = 0,1 нм. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ 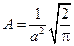 =7,9·1019 м-2
=7,9·1019 м-2 , описывающей поведение некоторой частицы, где r – расстояние этой частицы до силового центра; a = 0,1 нм. [1 балл] Ответ
, описывающей поведение некоторой частицы, где r – расстояние этой частицы до силового центра; a = 0,1 нм. [1 балл] Ответ  =4,2·1014 м-3/2
=4,2·1014 м-3/2 , где r – расстояние этой частицы до силового центра; a = 1010 м-1. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ
, где r – расстояние этой частицы до силового центра; a = 1010 м-1. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ  =7,9·1019 м-2
=7,9·1019 м-2 , где r – расстояние этой частицы до силового центра; a = 0,1 нм-2. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ
, где r – расстояние этой частицы до силового центра; a = 0,1 нм-2. Используя условие нормировки вероятностей, определить нормировочный коэффициент A. [1 балл] Ответ  =4,0·1012 м-3/2
=4,0·1012 м-3/2 определена в области 0≤ x ≤ ℓ. Используя это условие нормировки, определить нормировочный множитель A, если ℓ; =0,5 нм. [1 балл] Ответ
определена в области 0≤ x ≤ ℓ. Используя это условие нормировки, определить нормировочный множитель A, если ℓ; =0,5 нм. [1 балл] Ответ  =6,3·104 м-1/2
=6,3·104 м-1/2 , где r – расстояние этой частицы до силового центра; a = 0,1 нм. Определить среднее расстояние ‹r› частицы до силового центра. [2 балла] Ответ:
, где r – расстояние этой частицы до силового центра; a = 0,1 нм. Определить среднее расстояние ‹r› частицы до силового центра. [2 балла] Ответ:  = 0,05 нм
= 0,05 нм [2 балла] Ответ: 0,091
[2 балла] Ответ: 0,091 , где r – расстояние этой частицы до силового центра; a = 1 нм. Определить среднее расстояние ‹r› частицы до силового центра. [2 балла] Ответ:
, где r – расстояние этой частицы до силового центра; a = 1 нм. Определить среднее расстояние ‹r› частицы до силового центра. [2 балла] Ответ:  = 1,13 нм
= 1,13 нм , где r – расстояние электрона от ядра; a = 53 пм (первый боровский радиус). Определить среднее значение квадрата расстояния ‹r2› электрона до ядра в основном состоянии. [2 балла] Ответ:
, где r – расстояние электрона от ядра; a = 53 пм (первый боровский радиус). Определить среднее значение квадрата расстояния ‹r2› электрона до ядра в основном состоянии. [2 балла] Ответ:  = 8427 пм2
= 8427 пм2 , где r – расстояние этой частицы до силового центра; a =100 пм. Определить среднее значение квадрата расстояния ‹r2› частицы до силового центра. [2 балла] Ответ:
, где r – расстояние этой частицы до силового центра; a =100 пм. Определить среднее значение квадрата расстояния ‹r2› частицы до силового центра. [2 балла] Ответ:  = 2500 пм2
= 2500 пм2 0,44.
0,44. 1,3 нм.
1,3 нм. 5,19 эВ.
5,19 эВ. 2 нм ‑1.
2 нм ‑1. 4,48 эВ.
4,48 эВ. 29 эВ.
29 эВ. . [1 балл] Ответ:
. [1 балл] Ответ:  1,5 нм ‑1.
1,5 нм ‑1. . [1 балл] Ответ:
. [1 балл] Ответ:  7,5 эВ.
7,5 эВ. 25 эВ.
25 эВ. 21 нм-2.
21 нм-2.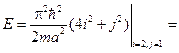 17,8 эВ.
17,8 эВ. 1,0 нм-2.
1,0 нм-2. 15 эВ.
15 эВ. 1,56 нм-2.
1,56 нм-2. 0,753 эВ.
0,753 эВ. 3,13 нм-2.
3,13 нм-2.
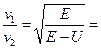 2.
2. 3.
3.
 1,34.
1,34. 0,023, где k = E / U.
0,023, где k = E / U. 0,2.
0,2. 0,71.
0,71. 0,17 нм.
0,17 нм. 21.
21.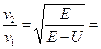 1,25.
1,25.
 1,5.
1,5.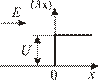
 0,5.
0,5.


