Краткое теоретическое введение
Изучение магнитного поля соленоида Цель работы Изучение распределения магнитного поля конечного соленоида при помощи явления электромагнитной индукции. Краткое теоретическое введение Соленоид – это цилиндрическая катушка, обмотка которой состоит из большого числа витков проволоки, образующих винтовую линию. Если витки расположены вплотную, то соленоид можно рассматривать как систему последовательно соединенных круговых токов, имеющих общую ось. Индукция магнитного поля
где L - длина соленоида, R –радиус его витков, Х – расстояние от края соленоида до исследуемой точки, I – сила тока, протекающего по виткам, n- число витков на единицу длина соленоида,
μ0 - магнитная постоянная. Единицей измерения индукции магнитного поля в системе СИ является «Тесла»: [B] = Тл Из выражения (1) следует,что индукция магнитного поля максимальна на оси соленоида в точке,соответсвующей его середине:
Если длина соленоида намного превышает радиус его витков,то соленоид можно условно считать бесконечно длинным.Магнитное поле внутри бесконечно длинного соленоида является однородным,при этом его индукция равна:
Распределение магнитного поля соленоида конечной длины является более сложным по сравнению с простейшим случаем бесконечно длинного соленоида. Для многих других конфигураций магнитного поля, теоретический расчет которых затруднителен, предпочтительней определять магнитную индукцию Величину
В настоящей работе в качестве контура используется измерительная катушка (ИК), состоящая из большого количества витков N. Возникающая в ней э.д.с. индукции складывается из э.д.с. отдельных витков,т.е.
где S –площадь поперечного сечения ИК. Если в обмотке соленоида протекает переменный ток, то магнитное поле, создаваемое этим током, также является переменным, т.е.
где В0 - амплитудное значение магнитной индукции,
Из формул (5) и (6) следует, что э.д.с. индукции, наведения ИК, изменяется во времени по закону: e = e0 sin(wt) (7)
где e0 - амплитудное значение э.д.с., равное e0 = NSwB0 = kB0, (8)
Коэффициент называется градуировочной постоянной измерительной установки.Ее можно определить экспериментально. Вольтметр, используемый для измерения э.д.с. индукции e, показывает эффективное значение переменного напряжения U, связанное с амплитудным значением э.д.с. (e0) соотношением:
Максимальному значению индукции магнитного поля в центре соленоида (2) соответствует максимальное эффективное значение напряжения:
Из формул (9) и (10) следует, что отношение эффективного напряжения в любой точке нахождения ИК к его максимальному эффективному значению в центре соленоида равно отношению магнитной индукции в этой точке к максимальной магнитной индукции в центре соленоида:
Поэтому распределение индукции магнитного поля соленоида можно изучать, не вычисляя градуировочную постоянную измерительной установки k.
|

 в любой точке соленоида равно векторной сумме индукций магнитных полей, создаваемых в данной точке всеми витками. Вектор магнитной индукций в точке, лежащей на оси соленоида конечных размеров, направлен вдоль оси, а его значение вычисляется по формуле:
в любой точке соленоида равно векторной сумме индукций магнитных полей, создаваемых в данной точке всеми витками. Вектор магнитной индукций в точке, лежащей на оси соленоида конечных размеров, направлен вдоль оси, а его значение вычисляется по формуле: , (1)
, (1) - относительная магнитная проницаемость среды,
- относительная магнитная проницаемость среды, . (2)
. (2) . (3)
. (3) . (4)
. (4) , (5)
, (5) , (6)
, (6) – циклическая частота переменного тока.
– циклическая частота переменного тока. . (9)
. (9)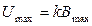 . (10)
. (10)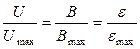 . (11)
. (11)


