Примеры решения задач. 1) Задача на применение закона Кулона.
1) Задача на применение закона Кулона. Два одинаковых маленьких шарика массой по 2г подвешены на шелковых нитях длиной 1м каждая в одной точке. После того как шарикам сообщили одинаковый положительный заряд, они разошлись на расстояние 4см. Определите величину заряда каждого шарика. Запишем краткое условие задачи.
Дано: СИ
r=4см =4·10-2м
q-?
Так как шарики находятся в покое, векторная сумма этих сил равна нулю: Проведем проверку размерности:
Произведем вычисления:
Ответ: 8,34нКл.
2) Задача на применение принципа суперпозиции.
Два заряда по 20мкКл расположены на расстоянии 6 см друг от друга. Найти напряженность в точке, удаленной на 5см от каждого заряда, если заряды одноименные. Запишем краткое условие задачи. Дано: СИ Решение:
q1= 2нКл = 2·10-9Кл q2= 2нКл = 2·10-9Кл a= 6см =6·10-2м b= 5см =5·10-2м Е-?
По принципу суперпозиции результирующая напряженность По теореме косинусов модуль результирующей напряженности
По формулам приведения
Проведем проверку размерности:
Произведем вычисления: Ответ: 11,5 кВ/м. 3) Задача на работу сил электрического поля. Шарик массой 10-4кг перемещается вдоль силовой линии однородного электрического поля из точки 1 с потенциалом 1000В в точку 2 с потенциалом равным 100В. Определите скорость шарика в точке 1, Запишем краткое условие задачи.
Дано: q=10-5Кл m=10-4кг φ1=1000В φ2=100В v2=20м/с v1-?
Проведем проверку размерности:
Произведем вычисления: Ответ: 14,8м/с
4) Задача на использование формул потенциальной энергии и емкости конденсатора.
Какую работу нужно совершить, чтобы удалить слюдяную пластинку из плоского конденсатора емкостью 10мкФ? Заряд конденсатора 100мкКл. Запишем краткое условие задачи.
Дано: СИ С1=10мкФ =10-5Ф Q=100мкКл =10-4Кл
А-?
где Отсюда
И искомая работа:
Проведем проверку размерности:
Произведем вычисления: Ответ: - 2,5мДж
5) Задача на применение закона Ома. Лампа подключена медными проводами к источнику тока с ЭДС 2 В и внутренним сопротивление 0,04 Ом. Длина проводов 4 м, их диаметр 0,8 мм. Напряжение на зажимах источника 1,98 В. Найти сопротивление лампы.
Запишем краткое условие задачи. Дано: СИ Е=2В r=0,05 Ом
d=0,8мм =8·10-4м Uвн=1,98В Rл-?
Тогда Проведем проверку размерности:
Произведем вычисления: Ответ: 3,33 Ом 6) Задача на определение потерь мощности. Ток мощностью 2·108Вт необходимо передать на расстояние 200км при напряжении 2·105В. Потери мощности на линии передачи не должны превышать 10%. Какого сечения нужно взять алюминиевый провод? Запишем краткое условие задачи.
Дано: СИ P=2·108Вт U=2·105В.
k=0,1 S-?
С учетом того, что ток в цепи Проведем проверку размерности:
Произведем вычисления:
Ответ: 5,6·10-4 м2.
7) Задача на применение закона Био-Савара-Лапласа. По квадратной рамке со стороной 0,2 м течет ток 4 А. Определить напряженность и индукцию магнитного поля в центре рамки. Запишем краткое условие задачи.
Дано: а = 0,2м I = 4 A B -? H -?
 , ,
здесь r = а/2 – расстояние от проводника до центра квадрата, α1 = 450, α2 = 1350. Тогда получим расчетную формулу для В:
Произведем вычисления:
Индукция поля и напряженность связаны соотношением: Отсюда Ответ: 22,6·10-6 Тл; 18 А/м.
8) Задача на применение закона Ампера.
Прямолинейный проводник массой 2 кг и длиной 59 см помещен в однородное магнитное поле перпендикулярно линиям индукции. Какой ток должен проходить по нему, чтобы он висел не падая? Индукция однородного магнитного поля равна 15 Тл.
Запишем краткое условие задачи.
Дано: СИ m=2кг
В=15Тл α=900 I-?
Проведем проверку размерности:
Произведем вычисления: Ответ: 2,2 А
9) Задача на силу Лоренца.
α-частица, ускоренная разностью потенциалов 250 В, влетает в однородное магнитное поле индукцией 25 мТл, перпендикулярно линиям магнитной индукции и движется по окружности. Найдите радиус окружности и период обращения α-частицы. Запишем краткое условие задачи.
Дано: СИ е=1,6·10-19Кл mp=1,67·10-27кг U=250B B=25мТл =25·10-3Тл α=900. R, T-?
В магнитном поле на движущуюся заряженную частицу действует сила Лоренца: Период обращения частицы найдем, разделив длину окружности на скорость частицы: Заряд α-частицы: Проведем проверку размерности:
Произведем вычисления: Ответ: 0,13 м; 5,2·10-6 с. 10) Задача на электромагнитную индукцию.
Катушка сопротивлением 100 Ом, состоящая из 1000 витков, внесена в однородное магнитное поле, так что линии магнитной индукции параллельны оси катушки. Площадь поперечного сечения катушки равна 5 см2. В течение некоторого времени индукция магнитного поля уменьшилась с 0,09 до 0,04 Тл. Какой заряд индуцирован в проводнике за это время? Запишем краткое условие задачи.
Дано: СИ R=100 Ом N=1000 S=5см2 =5·10-4м2 B1=0,09Тл B2=0,04Тл q-?
Приравниваем: По закону Фарадея ЭДС индукции, возникающая в катушке содержащей N витков: где Угол α между нормалью к плоскости контура и линией магнитной индукции по условию задачи равен нулю, поэтому С учетом этого
Проведем проверку размерности:
Произведем вычисления:
Ответ: 2,5·10-4 Кл
11) Задача на идеальный колебательный контур.
Колебательный контур состоит из конденсатора емкостью С=5 мкФ и катушки индуктивности L = 0,2 Гн. Определить максимальную силу тока I0 в контуре, если максимальная разность потенциалов на обкладках конденсатора U0 = 90 В. Активным сопротивлением проводов в контуре пренебречь. Запишем краткое условие задачи.
Дано: СИ L=0,2 Гн С=5 мкФ =5·10-6Ф U0= 90В
I0 -?
Полная энергия контура равна энергии конденсатора при максимальном значении U: Сила тока достигает максимального значения в момент разрядки конденсатора, при этом Следовательно, Откуда: Произведем вычисления: Ответ: 0,45 А
12) Задача на формулу Томсона. В колебательный контур включен конденсатор емкостью С=0,2 мкФ. Какую индуктивность L нужно включить в контур, чтобы получить в нам электромагнитные колебания частоты υ = 400Гц? Запишем краткое условие задачи.
Дано: СИ С=0,2 мкФ =0,2·10-6Ф υ= 400Гц
L -?
Следовательно, Откуда Произведем вычисления:
Ответ: 0,79 Гн.
|

 , сила Кулона
, сила Кулона  и сила натяжения нити
и сила натяжения нити 
 =1м
=1м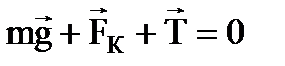 . Это возможно только в том случае, если равнодействующая силы тяжести и силы натяжения нити уравновешивается силой отталкивания:
. Это возможно только в том случае, если равнодействующая силы тяжести и силы натяжения нити уравновешивается силой отталкивания: 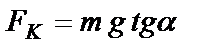 . По закону Кулона
. По закону Кулона 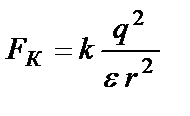 . Приравниваем правые части
. Приравниваем правые части 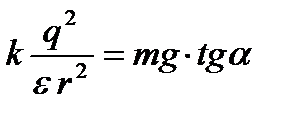 и
и  . Угол α найдем, зная, что
. Угол α найдем, зная, что  и тогда
и тогда  .
.
 .
. .
.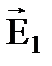 и
и  электрических полей, создаваемых зарядами q1 и q2 с учетом знаков зарядов.
электрических полей, создаваемых зарядами q1 и q2 с учетом знаков зарядов.

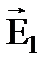

 .
.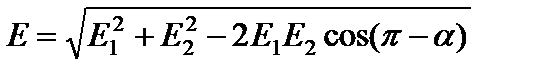 , где
, где , так как заряды по модулю равны и равны расстояния от зарядов до точки, в которой ищем результирующую напряженность. α -угол между векторами
, так как заряды по модулю равны и равны расстояния от зарядов до точки, в которой ищем результирующую напряженность. α -угол между векторами 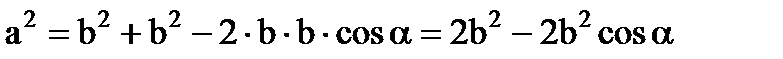

 .
.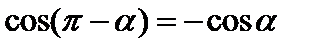 , следовательно
, следовательно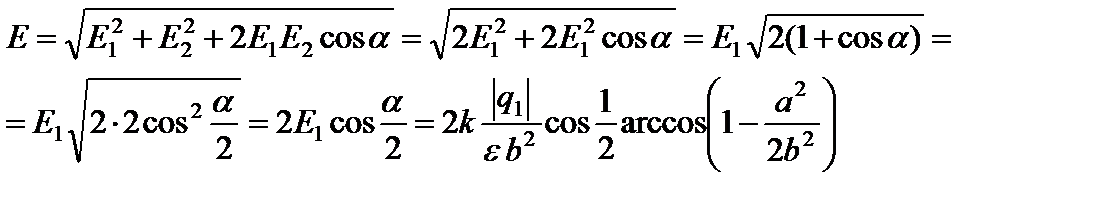

 .
. если в точке 2 его скорость 20м/с. Заряд шарика 10-5Кл.
если в точке 2 его скорость 20м/с. Заряд шарика 10-5Кл. :
: 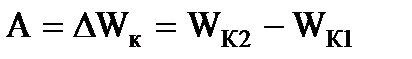 ,
, 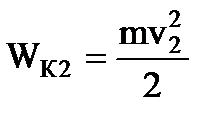 ,
,  -кинетические энергии шарика в точках 2 и 1 соответственно. С другой стороны работу поля можно найти через разность потенциалов:
-кинетические энергии шарика в точках 2 и 1 соответственно. С другой стороны работу поля можно найти через разность потенциалов: 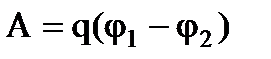 .
.  . Отсюда
. Отсюда  .
.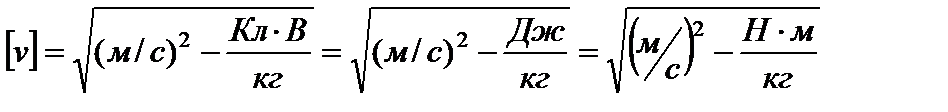 =
= 

 - потенциальная энергия конденсатора с пластинкой,
- потенциальная энергия конденсатора с пластинкой,  - его потенциальная энергия без пластинки. Заряд конденсатора при удалении пластинки не изменился, так как он отключен от источника тока. Емкость конденсатора с пластинкой
- его потенциальная энергия без пластинки. Заряд конденсатора при удалении пластинки не изменился, так как он отключен от источника тока. Емкость конденсатора с пластинкой  и без нее
и без нее 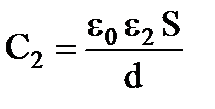 , ε1, ε2-диэлектрические проницаемости слюды и воздуха соответственно (из таблицы ε1=6, ε2=1). Разделим емкости конденсаторов друг на друга:
, ε1, ε2-диэлектрические проницаемости слюды и воздуха соответственно (из таблицы ε1=6, ε2=1). Разделим емкости конденсаторов друг на друга:  .
. .
.  .
. .
.

 , отсюда сила тока в цепи.
, отсюда сила тока в цепи.  . Общее сопротивление проводов и лампы
. Общее сопротивление проводов и лампы
 =4м
=4м , где
, где  , ρ-удельное сопротивление меди (из таблицы ρ=1,7·10-8Ом·м),
, ρ-удельное сопротивление меди (из таблицы ρ=1,7·10-8Ом·м), 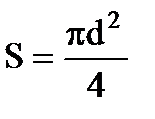 -площадь сечения провода, длина провода удваивается, так как провод двужильный. С другой стороны общее сопротивление цепи по закону Ома для однородного участка цепи:
-площадь сечения провода, длина провода удваивается, так как провод двужильный. С другой стороны общее сопротивление цепи по закону Ома для однородного участка цепи: 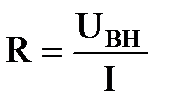 .
. .
.

 . С другой стороны мощность электрического тока, выделяемая на проводнике
. С другой стороны мощность электрического тока, выделяемая на проводнике 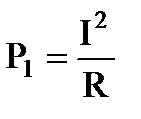 , отсюда
, отсюда  .
.
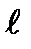 =200км =2·105м
=200км =2·105м , получим
, получим 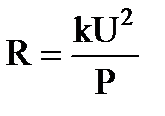 . Сопротивление проводов
. Сопротивление проводов  , ρ=2,8·10-8Ом·м – удельное сопротивление алюминия (из таблицы). Приравниваем два выражения для сопротивления
, ρ=2,8·10-8Ом·м – удельное сопротивление алюминия (из таблицы). Приравниваем два выражения для сопротивления 

 .
.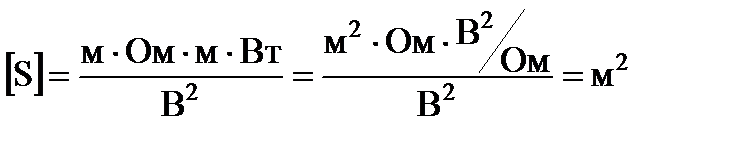


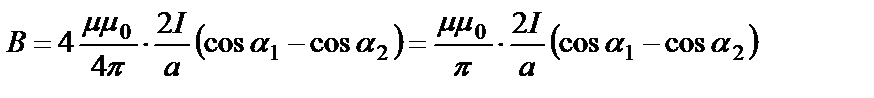

 .
.
 будет уравновешена силой Ампера
будет уравновешена силой Ампера  , т.е. модули этих сил
, т.е. модули этих сил  . Согласно закону Ампера
. Согласно закону Ампера  .
.  . Отсюда сила тока
. Отсюда сила тока 
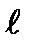 =59см =0,59м
=59см =0,59м .
.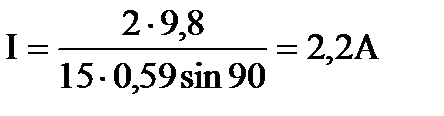 .
.

 .
. , угол α=900 и
, угол α=900 и  . Согласно второму закону Ньютона
. Согласно второму закону Ньютона 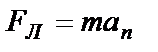 , где
, где  - центростремительное ускорение частицы, движущейся по окружности радиуса R. Получаем
- центростремительное ускорение частицы, движущейся по окружности радиуса R. Получаем  . Окончательно радиус окружности:
. Окончательно радиус окружности:  .
. .
. , ее масса
, ее масса 
 =
= 



 , где
, где  - ЭДС индукции. По определению сила тока
- ЭДС индукции. По определению сила тока  , где
, где 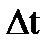 - время протекания заряда через поперечное сечение провода.
- время протекания заряда через поперечное сечение провода. . Отсюда
. Отсюда 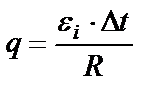 .
.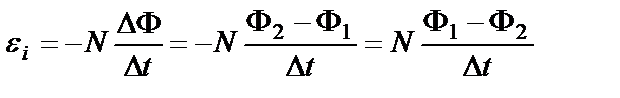 ,
, ,
,  .
. .
. .
.
 .
.
 .
. .
. .
. .
.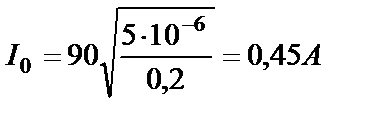 .
.
 .
Циклическая частота равна
ω = 2πυ
.
Циклическая частота равна
ω = 2πυ
 .
.
 .
.


