| Закон Кулона
где q1и q2 -величины точечных зарядов;
ε0 - электрическая постоянная;
ε - диэлектрическая проницаемость среды;
г-расстояние между зарядами.
| 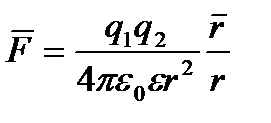
|
| Напряженность электрического поля
| 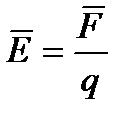
|
| Напряженность поля:
|
|
| Точечного заряда
| 
|
| Равномерно заряженной бесконечной плоскости
| 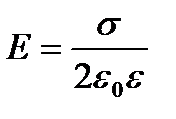
|
| Между двумя разноименно заряженными бесконечными плоскостями,
σ- поверхностная плотность заряда.
| 
|
| Работа перемещения заряда в электростатическом поле
где φ1 и φ2 – потенциалы начальной и конечной точек.
| 
|
| Потенциал поля точечного заряда
| 
|
| Связь между потенциалом и напряженностью
| 
|
| Сила притяжения между двумя разноименно заряженными обкладками конденсатора
Где S- площадь пластин
| 
|
| Электроемкость:
Уединенного проводника
| 
|
| Плоского конденсатора
| 
|
| Электроемкость батареи конденсаторов, соединенных:
Параллельно
|
|

|
| Последовательно
| 
|
| Энергия поля заряженного проводника
| 
|
| Энергия поля заряженного конденсатора
где V-объем конденсатора
| 
|
| Объемная плотность энергии электрического поля
| 
|
| Сила тока
| 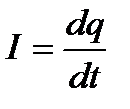
|
| Закон Ома:
в дифференциальной форме
| 
|
| в интегральной форме
где γ-удельная проводимость; ρ- удельное сопротивление; U-напряжение на концах цепи; R- сопротивление цепи; j-плотность тока.
|

|
| Закон Джоуля –Ленца в интегральной форме
| 
|
| Сопротивление однородного проводника
где l –длина проводника; S- площадь его поперечного сечения.
| 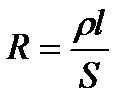
|
| Зависимость удельного сопротивления от температуры
Где α-температурный коэффициент сопротивления; t – температура по шкале Цельсия.
|

|
| Первое правило Кирхгофа:алгебраическая сумма токов, сходящихся в узле, равна нулю:
| 
|
| Второе правило Кирхгофа:в любом замкнутом контуре, произвольно выбранном в разветвлённой электрической цепи, алгебраическая сумма произведений сил токов Ii на сопротивление Ri соответствующих участков этого контура равна алгебраической сумме ЭДС ξk, встречающихся в этом контуре:
| 
|
| Сила Лоренца
Где v- скорость заряда q; В-индукция магнитного поля.
| 
|
| Сила Ампера
где I – сила тока в проводнике; dl-элемент длины проводника
| dF=I[dlxB]
|
| Магнитный момент контура с током
Где S –площадь контура
| рm =IS
|
| Механический момент, действующий на контур с током в магнитном поле
| М=[рmxB]
|
| Закон Био –Савара –Лапласа
где μ0- магнитная постоянная;
μ- магнитная проницаемость среды.
| 
|
| Магнитная индукция:
В центре кругового тока
| 
|
| Поля бесконечно длинного прямого тока
| 
|
| Поля, созданного отрезком проводника с током,
| 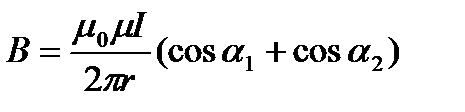
|
| Поля бесконечно длинного соленоида
Где R- радиус кругового тока; r- кратчайшее расстояние до оси проводника; n- число витков на единицу длины соленоида;
α1 и α2 – углы между отрезком проводника и линией, соединяющей концы отрезка с точки поля.
| 
|
| Сила взаимодействия двух прямолинейных бесконечно длинных параллельных проводников с током на единицу их длины
где r –расстояние между точками I1 и I2.
| 
|
| Работа по перемещению контура с током в магнитном поле
где Ф-магнитный поток через поверхность контура.
| 
|
| Магнитный поток однородного магнитного поля через площадку S
где α – угол между вектором В и нормалью к площадке.
| Ф=ВScosα
|
| Закон электромагнитной индукции
где N – число витков контура.
| 
|
| Потокосцепление контура с током
где L- индуктивность контура.
| 
|
| Электродвижущая сила самоиндукции
| 
|
| Индуктивность соленоида
где V- объем соленоида; n- число витков на единицу длины соленоида.
| 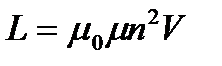
|
| Энергия магнитного поля
| 
|
| Объемная плотность энергии магнитного поля
| 
|
|
Электромагнитные колебания
| Т – период колебаний, с (секунда)
 φ0 - начальная фаза колебаний
w0 – циклическая частота, Гц
t – время, с
φ0 - начальная фаза колебаний
w0 – циклическая частота, Гц
t – время, с
|