Цифровой сигнал
Прежде чем рассмотреть процедуру его формирования сформулируем основные принципиальные отличия аналоговых и цифровых сигналов. Аналоговый сигнал представляет из себя бесконечную последовательность значений во времени. Действительно, рядом с каждой точкой на временной оси всегда можно выбрать соседнюю, сколь угодно близко расположенную к ней. Далее, каждое из этих значений может принимать любую величину в каком то интервале, причем число этих возможных значений тоже бесконечно. Например, значение вблизи 1 может быть 0,9;0,99; 0,999 и т.д. Поскольку число значений аналогового сигнала бесконечно во времени и по амплитуде, то его можно назвать бессчетным. Теперь ясно, какие требования нужно предъявить к цифровому сигналу. Число его возможных значений, как во времени, так и по амплитуде должно быть конечным, т. е ограничено каким-то числом. Цифровой сигнал должен быть счетным.
Рассмотрим процесс формирования цифрового сигнала (рисунок 4.1.2), который можно разбить на три этапа:
Рисунок 4.2 – Формирование цифрового сигнала а) дискретизация во времени; б) квантование по уровню; в) кодирование (импульсно-кодовая модуляция). На первом этапе вместо непрерывной функции времени SС(t) формируется совокупность дискретных отсчетов SС(t–кtд), взятых в равноотстоящих друг от друга моментах времени с интервалом tд. В соответствии с теоремой Котельникова этот интервал определяется верхней частотой в спектре сигнала ¦в tд£ Обосновать это неравенство можно следующим образом. Спектр дискретизируемого сигнала (рисунок 4.1.3) является периодической функцией частоты ¦ с периодом 1/tд. Для того чтобы лепестки этой функции не перекрывались необходимо, чтобы: 1/tд³2¦в.
Рисунок 4.3 – Спектр дискретного сигнала Если это неравенство не выполняется, спектр сигнала искажается в области высоких частот. Во временной области это приводит к тому, что наиболее быстрые изменения сигнала при дискретизации будут пропущены. Теорему Котельникова можно объяснить более простым образом. Возьмем гармоническую составляющую с частотой ¦в. Для ее описания с помощью дискретных отсчетов необходимо задать 2 отсчета на период. Полученный дискретный сигнал или сигнал с амплитудно-импульсной модуляцией (АИМ) может принимать в своих отсчетах любые непрерывные значения. Таким образом дискретный сигнал еще не стал цифровым. В качестве примера найдем время дискретизации для канала тональной частоты. При ¦в= 3.4 кГц выберем частоту дискретизации 4 кГц. Тогда tд =125 мкс. Чтобы число амплитудных значений было конечно, на втором этапе (рисунок 4.1.2, б) проводят операцию квантования. Она заключается в том, что значение отсчета сравнивается с некоторым уровнем, близким к нему, и приравнивается либо к величине этого уровня, либо к другой величине, связанной с ним. Такой величиной, например, может быть среднее значение между соседними уровнями. При равномерном квантовании расстояние между соседними уровнями (шаг квантования) D одинаков. Процесс квантования сопровождается искажениями сигнала, которые тем больше, чем больше D. Эти искажения можно охарактеризовать мощностью шумов квантования, которая пропорциональна величине (D/2)2. Поскольку отсчеты дискретного сигнала Sk являются случайной величиной, статистическое усреднение для равномерного квантования приводит к результату: Рш кв= В свою очередь шаг квантования D зависит от максимального значения сигнала Smax и числа уровней n. Число уровней квантования можно найти, задавая отношение сигнал-шум, если в качестве основного источника шума взять шумы квантования.
Если сигнал гармонический:
S = Sm cos w0t, то
В (4.3)и (4.4) - В соответствии с требованиями стандартов минимум качества обеспечивается при Но это соотношение должно выполняться для самого минимального входного сигнала. Если учесть динамический диапазон сигнала на входе и взять случай более высокого качества передачи, то число уровней n будет много больше 8. Так если D=40 дБ, то n=800, а разрядность кодера r=10. Приведенный пример указывает на избыточность, возникающую при формировании цифрового сигнала, поскольку нет необходимости большие значения входного сигнала передавать с такой же точностью, что и малые. Поэтому при квантовании применяют процедуру неравномерного квантования (рисунок 4.4), когда шаг квантования входного сигнала увеличивается с ростом сигнала. Эта процедура называется компрессией или сжатием динамического диапазона. На практике компрессию совмещают с кодированием, применяя кусочно-линейную характеристику вместо логарифмической (рисунок 4.5). При этом угол наклона отрезков прямых в каждом сегменте уменьшается в два раза. Применение неравномерного квантования позволяет ограничить число разрядов r=8.
Можно сделать вывод, что после операции квантования сигнал стал «счетным» как во времени, так и по амплитуде, т.е. он стал цифровым. Если значения уровней представлены в десятичной системе исчисления, то и цифровой сигнал будет представлен в десятичном коде. Такие сигналы широко применяются в ЦСП (многоуровневое кодирование). На третьем этапе сигнал Sкв(t), дискретный во времени и по амплитуде, с помощью импульсно-кодовой модуляции (ИКМ) преобразуется в цифровой код. Наиболее распространенным является двоичный цифровой код (рисунок 4.2, в). Особенностью этого кода, представленного набором электрических импульсов, является то, что длительность каждого импульса в кодовой комбинации ИКМ tик =
|


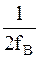 . (4.1)
. (4.1)
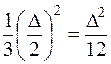 . (4.2)
. (4.2)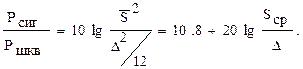 (4.3)
(4.3)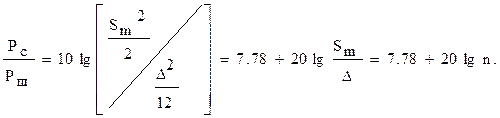 (4.4)
(4.4)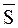 = среднее значение, а Sm – амплитуда сигнала.
= среднее значение, а Sm – амплитуда сигнала.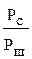 =26 дБ. Подставляя это значение в (4.4),найдем n=8.
=26 дБ. Подставляя это значение в (4.4),найдем n=8.
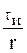 в r раз меньше длительности исходного импульса. Это приводит к соответствующему расширению спектра.
в r раз меньше длительности исходного импульса. Это приводит к соответствующему расширению спектра.



