Уравнения Максвелла в среде с высокой проводимостью
В уравнения Максвелла входит выражение для плотности тока в среде. В соответствии с нашим предположением, что объемные заряды отсутствуют, ток в среде является током проводимости, плотность которого пропорциональна скорости упорядоченного движения (дрейфа) носителей в веществе
здесь
В неподвижных проводниках дрейф носителей обусловлен обычно электрическими полями. В рассматриваемом случае проводники могут перемещаться, поэтому на носители действует еще и сила Лоренца, пропорциональная скорости их движения в данной системе отсчета. Скорость эта складывается из скорости движения проводников и скорости дрейфа. Полагая, что скорость дрейфа носителей много меньше скорости движения среды
Это позволяет записать закон Ома, учитывающий действие сторонних (неэлектрических) сил в дифференциальной форме
В случае среды, обладающей высокой проводимостью, заметная плотность тока возникает при малых силах, действующих на носители. В пределе можно считать, что эти силы пренебрежимо малы, что соответствует квазиравновесным состояниям носителей в веществе, когда
Это значительно упрощает уравнения Максвелла, поскольку позволяет исключить из них электрическое поле. В этом случае
4. Условия «вмороженности» силовых линий Напомним, что векторное поле, линии которого в любой момент проходят через одни и те же частицы среды, называется «вмороженненным». Условие вмороженности силовых линий магнитного поля в вещество имеет вид:
В веществе высокой проводимости скорость и напряженность магнитного поля связаны условием квазистатичности
Используем тождество
Из уравнений Максвелла
Вводя субстанциальную производную
Но это как раз условие «вмороженности» силовых линий поля в вещество, рассмотренное выше. Следовательно, силовые линии магнитного поля «вморожены» в несжимаемом веществе высокой проводимости.
|

 :
:
 - концентрация носителей заряда
- концентрация носителей заряда 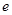 . В соответствии с законом Ома будем считать, что эта скорость пропорциональна сумме сил, действующих на носители в веществе со стороны поля:
. В соответствии с законом Ома будем считать, что эта скорость пропорциональна сумме сил, действующих на носители в веществе со стороны поля:
 , запишем соотношение для скорости дрейфа носителей в виде
, запишем соотношение для скорости дрейфа носителей в виде .
. .
. .
. и уравнение Максвелла приводит к условию квазистатичности
и уравнение Максвелла приводит к условию квазистатичности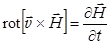

 .
. .
.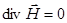 , а в случае несжимаемой жидкости и
, а в случае несжимаемой жидкости и  , поэтому для несжимаемой жидкости условие квазистатичности при высокой проводимости приводит к уравнению
, поэтому для несжимаемой жидкости условие квазистатичности при высокой проводимости приводит к уравнению .
. , нетрудно получить связь между вектором скорости и напряженности магнитного поля в несжимаемой среде (жидкости) высокой проводимости
, нетрудно получить связь между вектором скорости и напряженности магнитного поля в несжимаемой среде (жидкости) высокой проводимости ,
,


