Система уравнений самосогласованной задачи
Здесь необходимо указать каким образом предполагается сохранить и расширить достижения данного проекта (предусматривается ли продолжение работ по проекту.).
Система уравнений самосогласованной задачи До сих пор мы рассматривали движение вещества под действием объемных сил тяжести. Представляет интерес рассмотреть движение проводящего вещества в электромагнитном поле. Возникающие при движении токи порождают электромагнитные поля, которые могут оказывать влияние на движение среды, поэтому рассмотрим уравнения, описывающие самосогласованную систему среда + поле. Построим систему уравнений для описания самосогласованной задачи. Выделим 3 группы уравнений. I. Система уравнений механического движения сплошной среды состоит из двух уравнений: 1. Уравнения непрерывности
2. Уравнения Эйлера
Мы рассматриваем идеальную жидкость, для которой тензор напряжений имеет вид
II. Термодинамические уравнения, включающие термическое и калорическое уравнения состояния системы
а также уравнения процессов, происходящих со сплошной средой. В приложениях часто ограничиваются адиабатическими процессами, в которых теплообменом можно пренебречь, и влияние поля на состояние вещества мало, так что второе начало термодинамики
приводит к уравнению
III. Уравнения, определяющие поле в движущейся среде – уравнения Максвелла
Здесь мы предполагаем, что электрическая и магнитная проницаемость вещества равна единице, а плотность объемных зарядов в среде равна нулю. Если ограничиться квазистационарными процессами, то в уравнениях Максвелла можно пренебречь токами смещения по сравнению с токами проводимости ( Уравнения Максвелла устанавливают связь между плотностью тока проводимости и напряженностью магнитного поля, что позволяет определить плотность силы Ампера, действующей на проводящую среду, как функцию поля.
Уравнение Эйлера для квазистационарных процессов удобно записать в виде:
|



 , и плотность объемных зарядов которой равна нулю. Механическое воздействие поля на такую проводящую среду определяется силами Ампера, пропорциональными токам проводимости. Объемная плотность этих сил определяется выражением
, и плотность объемных зарядов которой равна нулю. Механическое воздействие поля на такую проводящую среду определяется силами Ампера, пропорциональными токам проводимости. Объемная плотность этих сил определяется выражением .
. ,
,  ,
,
 .
.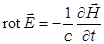 ,
,  ,
, ,
, 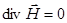 ,
, ). В этом случае уравнения Максвелла еще больше упрощаются, поскольку теперь можно положить
). В этом случае уравнения Максвелла еще больше упрощаются, поскольку теперь можно положить  .
. .
. .
.


