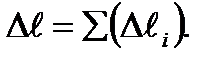Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука в 1678 году. Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению. Математически закон Гука можно записать в виде равенства: Коэффициент пропорциональности Е характеризует жесткость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода или модулем Юнга. Модуль упругости и напряжение выражаются в одинаковых единицах - Паскалях (Па). Значения Е, МПа, для некоторых материалов:
Чугун - (1, 5 ¸ 1, 6) .105 Сталь - (1, 96 ¸ 2, 16) .105 Медь - (1, 1 ¸ 1, 3) .105 Сплавы алюминия - (0, 69 ¸ 0, 71) .105 Дерево (вдоль волокон) - (0, 1 ¸ 0, 16) .105 Текстолит - (0, 06 ¸ 0, 1) .105 Капрон - (0, 01 ¸ 0, 02) .105
Если в формулу закона Гука подставим выражения
Произведение ЕА, стоящее в знаменателе, называется жесткостью сечения при растяжении и сжатии; оно характеризует одновременно физико-механические свойства материала и геометрические размеры поперечного сечения бруса. Отношение Приведенные выше формулы закона Гука применимы только для брусьев или их участков постоянного поперечного сечения, изготовленных из одного материала и при постоянной продольной силе. Для бруса, имеющего несколько участков, отличающихся материалом, размерами поперечного сечения, продольной силой, изменение длины всего бруса равно алгебраической сумме удлинений и укорочений отдельных участков:
|

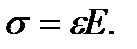
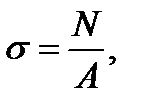
 , то получим:
, то получим: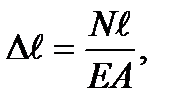
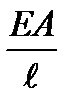 называется жесткостью бруса при растяжении или сжатии.
называется жесткостью бруса при растяжении или сжатии.