Потенциальная энергия деформации при растяжении
При статическом растяжении образца растягивающая сила F, медленно возрастающая от нуля до какого-то значения, удлиняет образец на величину
Если диаграмма растяжения построена в координатах (F,
Полная работа, затрачиваемая на разрушение образца, выражается площадью фигуры OABDN диаграммы растяжения, площадь треугольника NMD соответствует работе упругой деформации, исчезающей при разрыве образца. Удельной потенциальной энергией деформаций называется работа деформации, приходящаяся на единицу объема бруса:
2.6. Расчеты на прочность при растяжении и сжатии
Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации напряжения были меньше предельных. Отношение предельного напряжения к напряжению, возникающему в процессе работы детали, называют коэффициентом запаса прочности и обозначают буквой S:
Очевидно, что недостаточный коэффициент запаса прочности не обеспечит надежности конструкции, а чрезмерный запас прочности приведет к перерасходу материала и утяжелению конструкции. Отношение предельного напряжения к коэффициенту запаса прочности называют допускаемым напряжением и обозначают
Условие прочности детали конструкции заключается в том, что наибольшее возникающее в ней напряжение (рабочее) не должно превышать допускаемое:
Ориентировочные значения допускаемых напряжений на растяжение и сжатие для некоторых материалов приведены в таблице 2.1. Если напряжения при растяжении и сжатии различны, то их обозначают соответственно Расчетная формула при растяжении и сжатии имеет вид:
Таблица 2.1.
При расчете конструкций на прочность встречаются три вида задач, различающихся формой использования расчетной формулы: 1). Проектный расчет, при котором определяются размеры опасного сечения по формуле
2). Проверочный расчет, при котором определяется рабочее напряжение и сравнивается с допускаемым по формуле
3). Определение допускаемой нагрузки ведется по формуле
Задачи на расчет конструкций, в элементах которых внутренние силовые факторы не могут быть определены с помощью одних уравнений равновесия статики, называются статически неопределимыми. Для решения таких задач, помимо уравнений равновесия составляют уравнения перемещений или деформаций. Изменение температуры деталей вызывает изменение их размеров, в результате чего в статически неопределимых системах возникают дополнительные напряжения, называемые температурными. Рассмотрим невесомый стержень постоянного сечения площадью А, длиной
откуда получим, что реакции
Составим дополнительное уравнение, для чего мысленно отбросим правую заделку и заменим ее реакцией
(т. е. температурное удлинение стержня равно его укорочению под действием реакции Rb, так как связи полагаются абсолютно жесткими).
Рис. 2.4. Температурное удлинение
Определим температурные напряжения:
Для того чтобы, температурные напряжения не достигали значительных величин, один конец моста ставят на катки. В длинных трубопроводах, подвергающихся изменению температуры, делают компенсирующие устройства и т. д. Пример. Абсолютно жесткая балка, изображенная на рис. 2.5, шарнирно закреплена в стене и подвешена горизонтально на двух шарнирно закрепленных, вертикально расположенных стальных стержнях равной длины L = 2 м. В точке D на балку действует сила F = 20 кН. Площади поперечных сечений стержней равны:
Рис. 2.5. Решение. Рассматривая равновесие балки, отбросив связи и заменяяих реакциями, получаем три неизвестных: реакцию Для данной системы параллельных сил можно составить лишь два уравнения равновесия: уравнение проекций сил на вертикальную ось и уравнение моментов относительно какой-либо точки; следовательно, система статически неопределима. Для решения задачи необходимо составить дополнительное уравнение перемещений элементов конструкции, для чего изобразим ее в деформированном виде. Из подобия треугольников АСС ' и ABB ' получаем
отсюда
Составим уравнение моментов относительно точки А:
Упрощая последнее уравнение, получаем
По закону Гука
Разделим второе равенство на первое:
Разделим второе равенство на первое: так как, Находим Отсюда Определяем напряжения
|

 и при этом совершает работу W. Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми) можно считать, что
и при этом совершает работу W. Эта работа аккумулируется в деформируемом образце в виде потенциальной энергии деформации U, причем, пренебрегая незначительными потерями энергии (например, тепловыми) можно считать, что
 ), то площадь диаграммы выражает работу деформации. До предела пропорциональности работа выражается площадью треугольника OAK (см. рис. 2.3). Таким образом, потенциальная энергия упругой деформации стержня длиной
), то площадь диаграммы выражает работу деформации. До предела пропорциональности работа выражается площадью треугольника OAK (см. рис. 2.3). Таким образом, потенциальная энергия упругой деформации стержня длиной  постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна
постоянного поперечного сечения А при одинаковой во всех сечениях продольной силе N = F будет равна
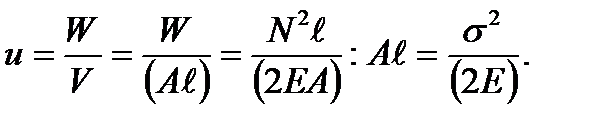
 где
где 



 и
и 





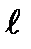 жестко защемленный по концам (рис. 2.4). При нагревании в стержне возникнут температурные напряжения сжатия. Определим эти напряжения. Составим для стержня уравнение равновесия:
жестко защемленный по концам (рис. 2.4). При нагревании в стержне возникнут температурные напряжения сжатия. Определим эти напряжения. Составим для стержня уравнение равновесия:
 и
и  равны. Применив метод сечений, установим, что продольная сила N в сечениях стержня равна неизвестным реакциям:
равны. Применив метод сечений, установим, что продольная сила N в сечениях стержня равна неизвестным реакциям:
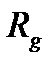 , тогда уравнение деформаций будет иметь вид
, тогда уравнение деформаций будет иметь вид
 где
где  – коэффициент линейного расширения материала стержня; укорочение под действием реакции
– коэффициент линейного расширения материала стержня; укорочение под действием реакции 
 Приравняем правые части этих равенств:
Приравняем правые части этих равенств: откуда
откуда 

 = 3 см2,
= 3 см2,  = 6 см2. Модуль упругости материала стержней Е = 2 .105 МПа, сила тяжести балки G = 40 кН. Определить напряжения в стержнях 1 и 2.
= 6 см2. Модуль упругости материала стержней Е = 2 .105 МПа, сила тяжести балки G = 40 кН. Определить напряжения в стержнях 1 и 2.
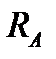 шарнира А и реакции
шарнира А и реакции  и
и  стержней 1 и 2.
стержней 1 и 2.





 а
а  то
то  откуда
откуда 
 и
и 

 и
и 
 и
и  в стержнях:
в стержнях:



