Теорема об изменении энергииУмножая уравнение Эйлера скалярно на вектор скорости, можно уравнение, описывающие изменение плотности энергии проводящей среды в магнитном поле:
Левая часть этого уравнения преобразуется к виду:
Для преобразования последнего слагаемого воспользуемся уравнением непрерывности:
В итоге левая часть уравнения принимает вид:
Для вычисления мощности поверхностных сил давления в среде
которое с учетом уравнения непрерывности можно записать в виде:
Из этого выражения с учетом уравнения непрерывности получаем
Отсюда для адиабатических процессов
Выражение для мощности силы Ампера также удобно преобразовать, учитывая свойства смешанного произведения векторов:
В рассматриваемом квазистатическом случае для вещества высокой проводимости
Учитывая тождество выражение для мощности силы Ампера можно представить в виде:
Равенства (а), (б) и (в) приводят к уравнению
которое можно рассматривать, как уравнение для изменения плотности энергии вещества и поля:
Здесь
|
.
.
.
(а)
воспользуемся первым началом термодинамики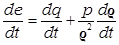
,
.
.
мощность сил определяется выражением
. (б)
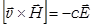, так что
.
и уравнение Максвелла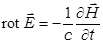 
,
. (в)
,
- плотность энтальпии, а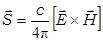 
- плотность потока энергии поля.
