Расчет балок балочной клетки нормального типа
1. Преподаватель говорит о том что настало время свести различные стороны проблематики воедино, чтобы продвинуться дальше в изучении темы (в разрешении проблемы). 2. Учащиеся совместно с преподавателем выделяют несколько аспектов, которые фиксируются на листе ватмана в указанной форме (см. с. 46). 3. Эти аспекты «вырезаются» и раздаются группам. 4. Задача состоит в том, чтобы записать сведения, связанные с аспектом проблемы (на обратной стороне листа). Перед тем как записать, нужно ознакомиться с предыдущими записями. 5. Каждая группа (или каждый ученик, если преподаватель хочет непременно задействовать всех), должна, за определенное время что-то отразить в как можно большем числе аспектов. 6. Затем обсуждаются различные варианты и формулируем исследовательские задачи. Самое главное — четко сформулировать аспекты темы. Несомненно, данный раздел не исчерпывает всех возможностей работы с учебным содержанием, и каждый творческий педагог приведет приемы, которые он использует со своими учениками для работы с учебным содержанием, которое применяется в курсе изучения учебных предметов. Но предложенная систематизация приемов может помочь подобрать наиболее эффективные из них для определенного вида учебного текста, разнообразить деятельность учащихся на уроке и дома, активизировать процессы их мышления. И, наконец, последнее: большинство приемов, указанных в данном разделе, способствуют развитию правого полушария головного мозга обучающихся. Одним из существенных недостатков современной системы образования является ее жесткая ориентация на левополушарных детей. Левое полушарие головного мозга человека обрабатывает данные в виде букв, цифр, слов и абстрактных идей, а правое отвечает за восприятие образов в целом, без участия слов. Приемы работы, особенно в учебных предметах, построенных в логике наук (например, биология, математика, физика и т. д.), как правило, ориентированы на решение линейных задач, основанных на логической последовательности и жестко заданных алгоритмах, то есть на работу левого полушария головного мозга. Большинство учеников, которые, плохо учатся, а то и относятся к категории необучаемых детей, имеют в качестве ведущего правое полушарие, и потому плохо справляются с заданиями, в которых работать приходится только левому полушарию мозга. Это не означает, что так называемые правополушарные люди не используют в своей жизни левое полушарие, но обучение, которое строится только на его работе, очень затрудняет их успешность, так как требует значительных усилий и все равно при этом качество выполнения подобных заданий у них невысоко. Таким образом, использование разнообразных приемов при работе с учебным содержанием позволяет сделать образовательный процесс более индивидуализированным, обеспечить максимальное развитие способностей каждого учащегося и повысить качество современного образования, что очень важно для профильного обучения. Примеры расчета конструкций балочной клетки Расчет балок балочной клетки нормального типа 4.1.1. Расчет балки настила прокатного профиля Для первого варианта принимаем толщину стального настила равную tn = 10 мм при временной нагрузке pn = 24 кН/м2. В связи с требованием к жесткости настила должно выполняться условие gn= tn*ρ=0,01*78,5=0,785 кН/см2 – нормативная постоянная нагрузка от веса настила, кН/см2 при удельном весе стали ρ=78,5 кН/см3; qn=gn+ pn=0,785+24=24,785 кН/м2=0,0024785 кН/см2.
ln/tn =(4*150/15)*(1+72*22600/1504*0,0024785)=91,9. В соответствии в вышеизложенным требуемый пролет настила принимается равным шагу балок настила, l = (ln/tn)* tn=91,9·10= 919 мм. Принимаем предварительно l = 900 мм. Далее вычисляется требуемое количество промежутков между балками, которое принимается нечетным:
Для подбора сечения балки настила необходимо определить нагрузку на эту конструкцию. Нормативная равномерно распределенная нагрузка на единицу длины балки равна qn = (gn + pn)· l, где gn – нормативная нагрузка от веса настила; gn = t·ρ = 0,01·78,5 = 0,785 кН/м2; t = 0,01 м; ρ = 78,5 кН/м3 – удельный вес стали; pn = 24 кН/м2; l – принятый шаг балок настила, м. qn = (0,785 + 24)*0,9 = 22,31 кН/м. Расчетная равномерно распределенная нагрузка на единицу длины балки равна q = (gn·γfg + pn ·γfp)· l, где γfg = 1,05 – коэффициент надежности по нагрузке для стали; γfp = 1,2 – коэффициент надежности по нагрузке для временной нагрузки при pn > 2 кН/м2 . q = (0,785*1,05 + 24*1,2)*0,9 = 26,66 кН/м. Определяем величину максимального изгибающего момента в балке настила:
Требуемый момент сопротивления балки настила определяется по формуле Принимаем двутавр № 40 с Wx = 953 см3, Ix = 19062 см4, ρ = 57 кгс/м согласно ГОСТ 8239-72. Проверка принятого сечения выполняется: а) на прочность при упругой стадии работы где γc = 1 – для балок прокатного профиля; Mmax – максимальный изгибающий момент, кН·м; Wx – момент сопротивления балки настила по сортаменту;
б) на жесткость от действия нормативных нагрузок при упругой работе материала прогиб от действия нормативных нагрузок равен
В = 7,7 м = 770 см; E = 2,06·104 кН/см2 – модуль упругости стали; Ix = 19062 см4 – осевой момент инерции выбранного двутавра;
Согласно требованиям главы 15 и прил. Е СП 20.13330.2012 «Нагрузки и воздействия» или по табл. Б.5 прил. Б предельно допустимый прогиб для прокатных балок равен
|

 где nо =
где nо = 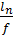 =150 – отношение пролета настила к его предельному прогибу; qn – нормативная временная нагрузка на настил, кН/см2;
=150 – отношение пролета настила к его предельному прогибу; qn – нормативная временная нагрузка на настил, кН/см2; =2,06*104/(1-0,32)=2,26*104 кН/см2;
=2,06*104/(1-0,32)=2,26*104 кН/см2; 900*9 = 8100 мм; 450*2 = 900
900*9 = 8100 мм; 450*2 = 900 где l = В = 7,7 м;
где l = В = 7,7 м; кН·м.
кН·м. где Ry = 240 МПа = 24 кН/см2 – для фасонного проката из стали С 245;
где Ry = 240 МПа = 24 кН/см2 – для фасонного проката из стали С 245; 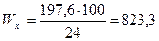 см3.
см3.
 – условие выполняется, прочность достаточна;
– условие выполняется, прочность достаточна; где qn =22,3 кН/м = 0,223 кН/см – нормативная равномерно распределенная нагрузка на единицу длины балки;
где qn =22,3 кН/м = 0,223 кН/см – нормативная равномерно распределенная нагрузка на единицу длины балки; см;
см; см.
см.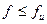 , 2,6 см < 3,85 см – условие выполняется, жесткость достаточна. Окончательно принимаем I № 40.
, 2,6 см < 3,85 см – условие выполняется, жесткость достаточна. Окончательно принимаем I № 40.


