Проверка гипотезы о нормальности распределения оставшихся результатов измерений.Так как n=22 лежит в интервале Применяя критерий 1, вычислим статистический коэффициент:
Подставив численные значения в формулу (2.4), получим:
Задаемся доверительной вероятностью
Так как Применяя критерий 2 (проверяем граничные условия), задаемся доверительной вероятностью
Для вероятности
Рассчитываем доверительный интервал:
Подставив численные значения в формулу (2.5), получим:
Так как ни одна разность
|
, то для проверки применяем составной критерий.
. (2.4)
.
, тогда уровень значимости 
. По таблицам (приложение Г) [1] определяем квантили распределения для 
и 
. В таблице отсутствуют данные для 
и 
.
(
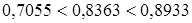), то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными.
и для уровня значимости 
с учетом 
и 
:
и 
.
(приложение Б) [1] определяем значение: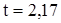
.
. (2.5)
.
не превосходит 
, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными и закон можно признать нормальным с вероятностью 
. В данном случае с вероятностью 
.
