Для проверки правильности выбора вида уравнения регрессии будем использовать непараметрический критерий серий и инверсий:
– рассчитываем отклонения экспериментальных значений 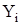 от соответствующих значений
от соответствующих значений  , рассчитанных для того же аргумента
, рассчитанных для того же аргумента  по полученному уравнению регрессии (табл. 5.2);
по полученному уравнению регрессии (табл. 5.2);
– строим в осях координат  и
и  полученные значения
полученные значения 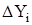 для соответствующих
для соответствующих  (рис. 5.2);
(рис. 5.2);

|
Рисунок 5.2 – Зависимость 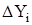 от от 
|
– записываем последовательность значений 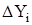 по мере возрастания
по мере возрастания  ,
,  (табл. 5.3);
(табл. 5.3);
– рассчитываем число серий 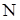 в полученной последовательности
в полученной последовательности  (под серией понимается последовательность отклонений одного знака, перед и после которой следует отклонение противоположного знака или нет вообще никаких отклонений) (табл. 5.3):
(под серией понимается последовательность отклонений одного знака, перед и после которой следует отклонение противоположного знака или нет вообще никаких отклонений) (табл. 5.3):
 ;
;
Таблица 5.2 – Отклонения экспериментальных значений 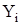 от соответствующих значений
от соответствующих значений  , рассчитанных для того же аргумента
, рассчитанных для того же аргумента  по уравнению регрессии (5.7)
по уравнению регрессии (5.7)
| Xi
|
|
|
|
|
|
|
|
|
|
|
| Yi
|
|
|
|
|
|
|
|
|
|
|
| Ypi
| 405,870
| 415,593
| 425,316
| 435,039
| 444,762
| 454,485
| 464,208
| 473,931
| 483,654
| 493,377
|
| ∆Yi
| -0,870
| 2,407
| 5,684
| 6,961
| 4,238
| 1,515
| 3,792
| 1,069
| 1,346
| -1,377
|

|
|
|
|
|
|
|
|
|
|
|
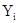
|
|
|
|
|
|
|
|
|
|
|
| Ypi
| 16,950
| 114,180
| 211,410
| 308,640
| 405,870
| 503,100
| 600,330
| 697,560
| 794,790
| 892,020
|

| -6,950
| -4,180
| -6,410
| 3,360
| -0,870
| 1,900
| 1,670
| -1,560
| 0,210
| -12,020
|
Примечания: 1. Значения  определялись по формуле (5.7). 2. Значения определялись по формуле (5.7). 2. Значения  определялись по формуле: определялись по формуле:  . .
|
Таблица 5.3 – Последовательность значений  по мере возрастания
по мере возрастания  ,
, 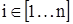
| Xi
|
|
|
|
|
|
|
|
|
|
|
| Yi
|
|
|
|
|
|
|
|
|
|
|
| ∆Yi
| -6,950
| -4,180
| -6,410
| 3,360
| -0,870
| 2,407
| 5,684
| 6,961
| 4,238
| 1,515
|
| Xi
|
|
|
|
|
|
|
|
|
|
| |
| Yi
|
|
|
|
|
|
|
|
|
|
| |
| ∆Yi
| 3,792
| 1,069
| 1,346
| -1,377
| 1,900
| 1,670
| -1,560
| 0,210
| -12,020
|
| |
– задаемся доверительной вероятностью  ,
,  (для
(для  ) и по таблице (приложение Ж) [1] определяем допустимые границы:
) и по таблице (приложение Ж) [1] определяем допустимые границы:
 ,
,  ;
;
– рассчитываем число инверсий  в полученной последовательности
в полученной последовательности  (под инверсией понимается событие, заключающееся в том, что
(под инверсией понимается событие, заключающееся в том, что  при
при  ):
):
 , (5.8)
, (5.8)
где  это число инверсий j-го члена последовательности, т.е. число членов последовательности, которые, будучи расположенными в последовательности после j-го члена, имеют меньшее, чем
это число инверсий j-го члена последовательности, т.е. число членов последовательности, которые, будучи расположенными в последовательности после j-го члена, имеют меньшее, чем  значение;
значение;
 ;
;
– задаемся доверительной вероятностью  ,
,  (для
(для  ) и по таблице (приложение И) [1] определяем допустимые границы:
) и по таблице (приложение И) [1] определяем допустимые границы:
 ,
,  .
.
Так как  (
(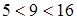 ) и
) и  (
(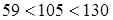 ), то с вероятностью
), то с вероятностью  можно считать, что отклонения экспериментальных значений
можно считать, что отклонения экспериментальных значений  , от соответствующих значений
, от соответствующих значений  найденного уравнения регрессии являются случайными, не содержат аддитивного, мультипликативного или колебательного трендов, т.е. рассчитанное уравнение регрессии достоверно описывает экспериментально исследуемую зависимость между величинами
найденного уравнения регрессии являются случайными, не содержат аддитивного, мультипликативного или колебательного трендов, т.е. рассчитанное уравнение регрессии достоверно описывает экспериментально исследуемую зависимость между величинами  и
и 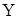 . Эта зависимость описывается уравнением (5.7).
. Эта зависимость описывается уравнением (5.7).
Определение уравнения регрессии  .
.

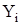 от соответствующих значений
от соответствующих значений  , рассчитанных для того же аргумента
, рассчитанных для того же аргумента  по полученному уравнению регрессии (табл. 5.2);
по полученному уравнению регрессии (табл. 5.2); и
и  полученные значения
полученные значения 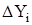 для соответствующих
для соответствующих 
 (табл. 5.3);
(табл. 5.3);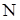 в полученной последовательности
в полученной последовательности  (под серией понимается последовательность отклонений одного знака, перед и после которой следует отклонение противоположного знака или нет вообще никаких отклонений) (табл. 5.3):
(под серией понимается последовательность отклонений одного знака, перед и после которой следует отклонение противоположного знака или нет вообще никаких отклонений) (табл. 5.3): ;
;
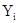

 определялись по формуле (5.7). 2. Значения
определялись по формуле (5.7). 2. Значения  .
.
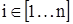
 ,
,  (для
(для  ) и по таблице (приложение Ж) [1] определяем допустимые границы:
) и по таблице (приложение Ж) [1] определяем допустимые границы: ,
,  ;
; в полученной последовательности
в полученной последовательности  при
при  ):
): , (5.8)
, (5.8) это число инверсий j-го члена последовательности, т.е. число членов последовательности, которые, будучи расположенными в последовательности после j-го члена, имеют меньшее, чем
это число инверсий j-го члена последовательности, т.е. число членов последовательности, которые, будучи расположенными в последовательности после j-го члена, имеют меньшее, чем  значение;
значение; ;
; ,
,  .
. (
(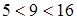 ) и
) и  (
(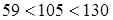 ), то с вероятностью
), то с вероятностью 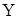 . Эта зависимость описывается уравнением (5.7).
. Эта зависимость описывается уравнением (5.7).  .
.


